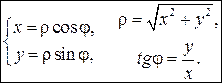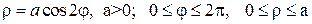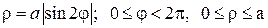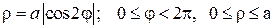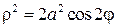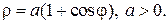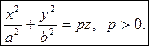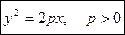Уравнение астроиды в полярной системе координат

Семейство роз Гранди

Уравнение имеет вид:

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

Рисунок 2 — роза с 16 лепестками ρ=sin8φ

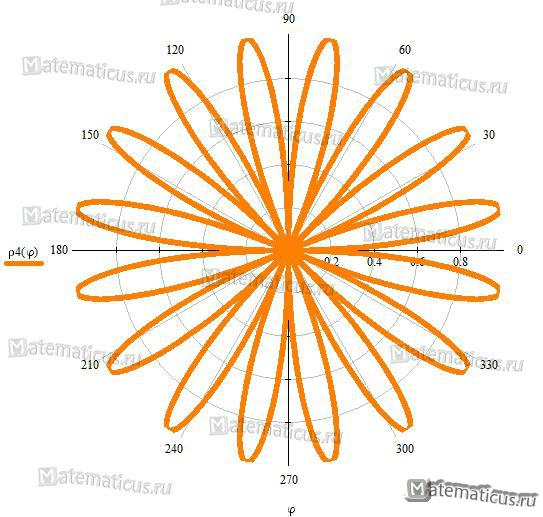
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

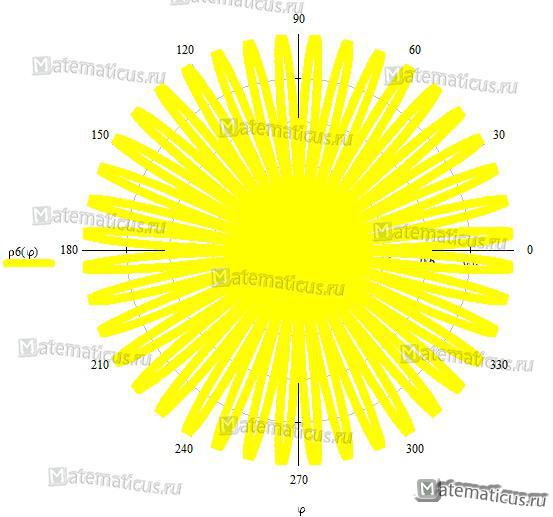
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

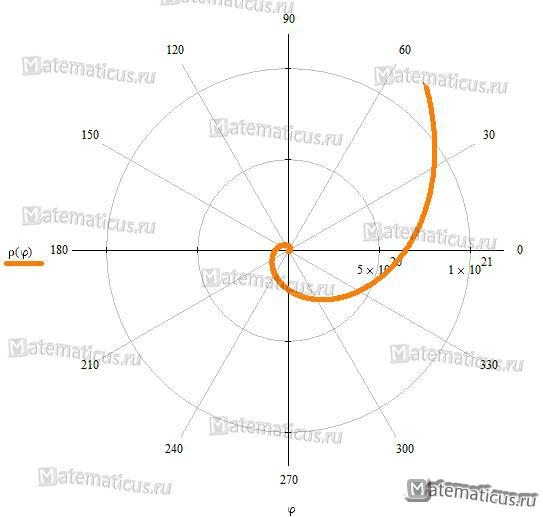
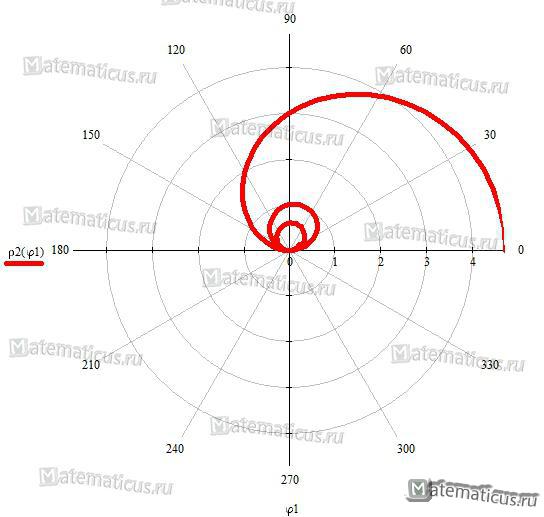
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

Видео:Построение кривой в полярной системе координатСкачать

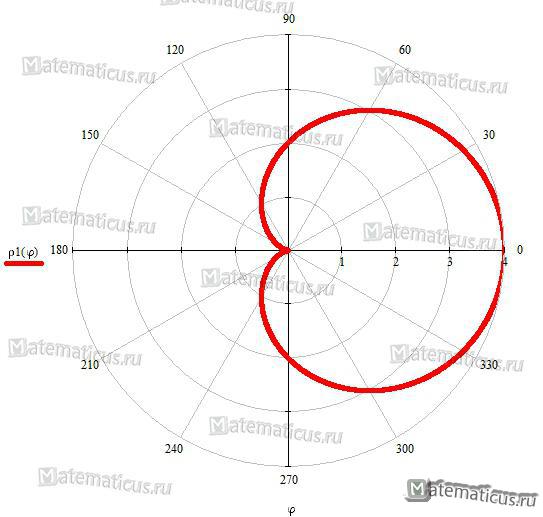
Кардиоида

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

Видео:Полярная система координатСкачать

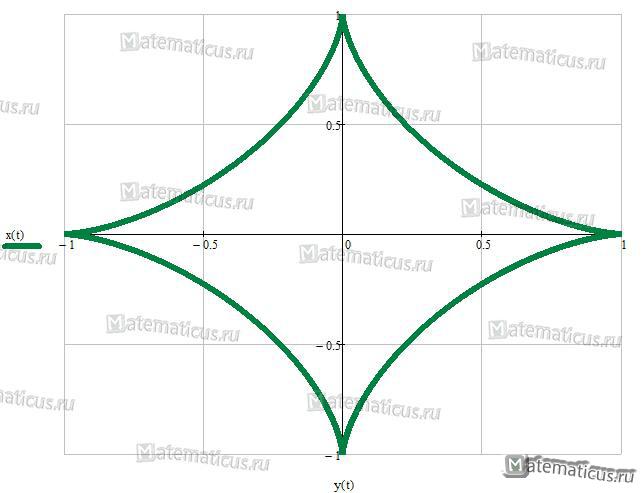
Астроида

Уравнение астроиды (перев. греч. звезда и вид) :

x 2/3 + y 2/3 = a 2/3

Видео:Полярная система координат.Скачать

Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот) :

y 2 (a — x)= x 2 (a + x)

Уравнение строфоиды в полярной системе координат:

Видео:Занятие 01. Часть 3. Полярная система координатСкачать

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Декартов лист

Уравнение декартова листа :

x 2 + y 2 — 3axy = 0

Уравнение декартова листа в полярной системе координат:

Видео:Видеоурок "Полярная система координат"Скачать

Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :

Параметрическое уравнение циссоиды:

x = a t 2 /(1 + t 2 )

x = a t 3 /(1 + t 2 )

Уравнение циссоиды в полярной системе координат:

Видео:Полярная система координатСкачать

Циклоида

Параметрическое уравнение циклоиды :

Видео:Глаза гипножабы и площадь фигур в полярной системе координатСкачать

Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

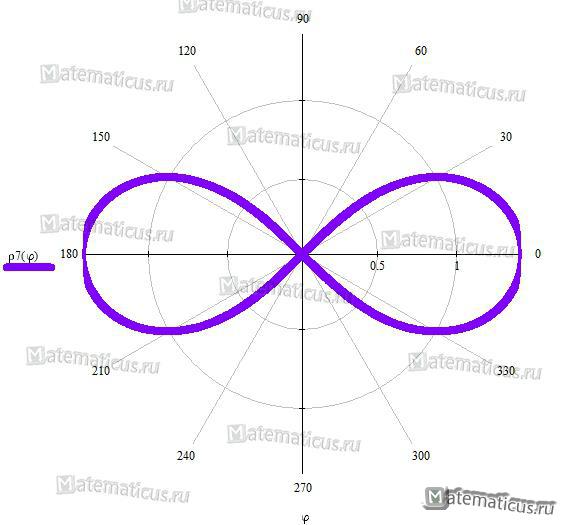
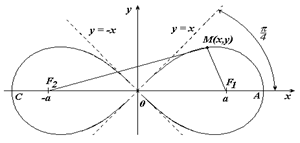
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Уравнение лемниската Бернулли в полярных координатах:

Архимедова спираль рассмотрена здесь подробно.

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

Видео:Площадь фигуры, заданной в полярной системе координатСкачать

Линии в полярной системе координат

Полярные координаты

, .

Связь полярных координат с декартовыми

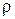
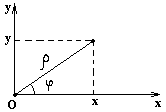M(x,y) и M( ,j):

Окружности

а=const >0.

, а=const >0.

Спирали

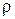
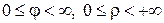
Архимедова спираль: =аj, .

Гиперболическая спираль: , a > 0.

Логарифмическая спираль: .

Розы

Двухлепестковые розы: .

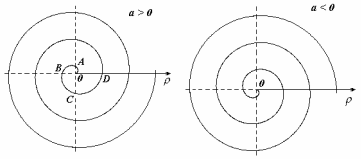
Четырехлепестковые розы a > 0

Лемниската Бернулли

Вершины кривой находятся в точках

Площадь каждой петли S=a 2 .

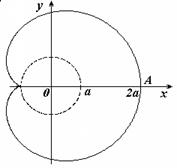
Кардиоида

В полярных координатах

Вершина кардиоиды находится в точке А(2а,0).

Укажем, что площадь кардиоиды , а длина L=8a.

Параметрическое задание линий

Окружность

— параметрические уравнения окружности.

Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:

.

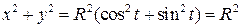
Циклоида

где .

При получаем первую арку циклоиды. Укажем, что длина дуги ОА₁О₁=8а, а площадь одной арки S=3 a 2 .

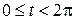
Астроида

где

В декартовых координатах уравнение астроиды

Длина астроиды L=6R, а площадь, ограниченная астроидой S=3pR 2 /8.

IV. Поверхности второго порядка

Эллипсоид

.

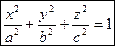
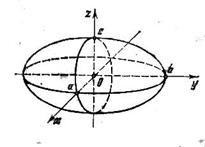Гиперболоиды

Однополостный гиперболоид

.

Двуполостный гиперболоид

.

Параболоиды

Эллиптический параболоид

Гиперболический параболоид

Конус

.

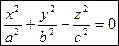
Цилиндры

Эллиптический цилиндр

.

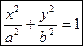
Гиперболический цилиндр

.

Параболический цилиндр

1. Ильин В.А. Аналитическая геометрия / В.А.Ильин, Э.Г.Позняк.
М.: Наука, ГФМЛ, 1988.

2. Бугров Е.С. Элементы линейной алгебры и аналитической геометрии /
Е.С. Бугров, С.М. Никольский. М.: Наука, 1984.

3. Бугров Е.С. Высшая математика: Задачник / Е.С. Бугров, С.М. Никольский. М.: Наука, 1982.

4. Сборник задач по математике для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. — 4-е изд., перераб. и доп. — М.: Физматлит, 2003. — 288 с.: ил.; 21 см. — ISBN 5-940520-34-0.

5. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры /
Д.В.Беклемишев. М.: Наука, 1984.

6. Наумов В.А. Руководство к решению задач по линейной алгебре и аналитической геометрии / В.А.Наумов. М.: Наука, 1993.

7. Фадеев Д.К. Сборник задач по высшей алгебре / Д.К. Фадеев, Н.С. Соминский. М.: Наука, 1997.

8. Беклемишева Л.А. Сборник задач по аналитической геометрии и линейной алгебре / Л.А. Беклемишева, А.Ю. Петрович, И.А. Чубаров. М.: Наука, 1987.

9. Кузнецов Л.А. Сборник заданий по высшей математике / Л.А. Кузнецов М.: Высшая школа, 1994.

10. Минорский В.П. Сборник задач по высшей математике / В.П. Минорский. М.: Физматгиз, 1961.

11. Клетенник Д.В. Сборник задач по аналитической геометрии /
Д.В. Клетенник. М.: Наука, 1986.

12. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии /
О.Н. Цубербиллер. М.: Наука, 1970.

13. Косторкин А.И. Линейная алгебраическая геометрия / А.И. Косторкин,
Ю.И. Манин. М.: Наука, 1986.

14. Бахвалов С.Б. Сборник задач по аналитической геометрии /
С.Б. Бахвалов, П.С. Моденов, А.С. Пархоменко. М.: Наука, 1964.

Соболев Александр Борисович

Вигура Марина Александровна

Рыбалко Александр Федорович

Рыбалко Наталья Михайловна

Трояновская Людмила Юрьевна

Кассандров Игорь Николаевич

Дисциплина: ЕН.Ф.01 Математика. алгебра и геометрия

Модуль 2: Векторная алгебра. Геометрия: аналитическая геометрия в пространстве, на плоскости, кривые второго порядка, поверхности.

Подписано в печать Формат 60×84 1/16

Бумага писчая Плоская печать Усл.печ.л. 3,13

Уч.-изд.л. 2,6 Тираж Заказ Цена “C”

Редакционно-издательский отдел ГОУ ВПО УГТУ–УПИ

620002, Екатеринбург, ул. Мира, 19

ООО «Издательство УМЦ УПИ»620002, Екатеринбург, ул. Мира, 17

Видео:Скорость и ускорение точки в полярных координатахСкачать

Уравнения кривых. Астроида.

Астроида – плоская кривая, которую формирует траектория точки, расположенной на окружности радиуса r, катящейся без трения по внутренней стороне неподвижной окружности радиуса R = 4r.

Параметрическое уравнение:

Уравнение в алгебраическом виде:

Длина дуги от точки с 0 до t ≤ π/2:

.

Длина всей кривой равна 6R.

Радиус кривизны описывается формулой:

.

Площадь, ограниченная кривой представлена такой формулой:

.

Объем тела вращения относительно любой координатной оси описан формулой:

.

🔥 Видео

§30 Уравнения кривых второго порядка в полярных координатахСкачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Оператор Лапласа в полярных координатахСкачать

Описание движения планет в полярной системе координатСкачать

Полярные в декартовыеСкачать

Занятие 01. Часть 1. Полярная система координатСкачать

§52 Полярная система координатСкачать

Полярная система координат на плоскостиСкачать

Линии в полярных координатах и параметрически заданныеСкачать