Семейство роз Гранди
Уравнение имеет вид:
a — радиус лепестка;
k — положительный параметр, отвечает за количество лепестков.
Рисунок 1 — роза с тремя лепестками ρ=sin3φ
Рисунок 2 — роза с 16 лепестками ρ=sin8φ
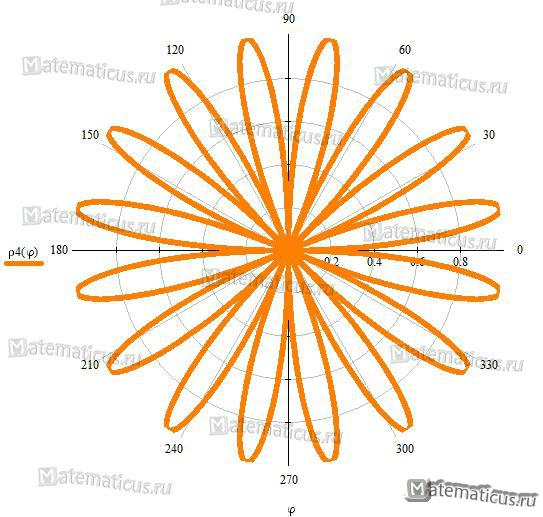
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ
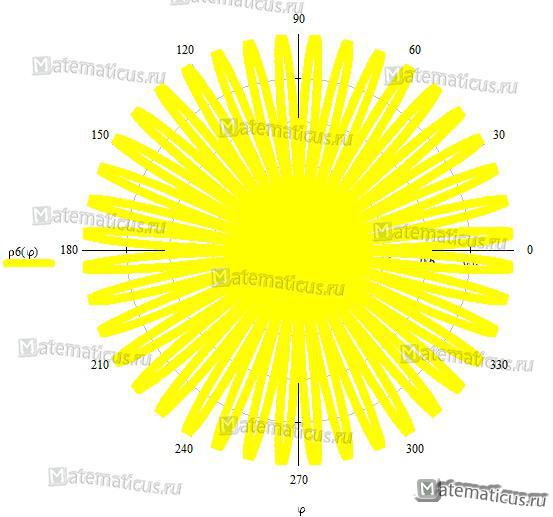
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ
Видео:Площадь Астроиды.АстроидаСкачать

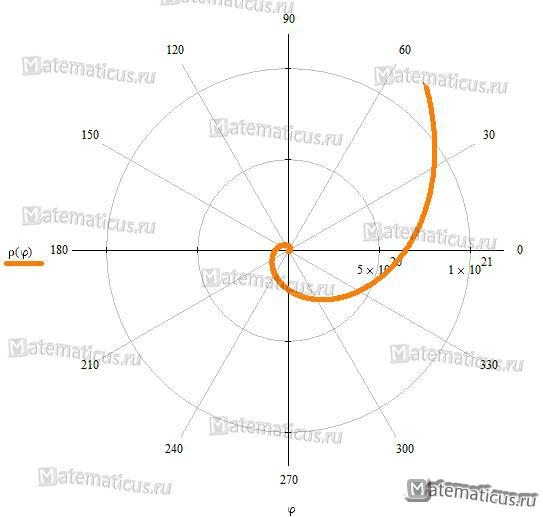
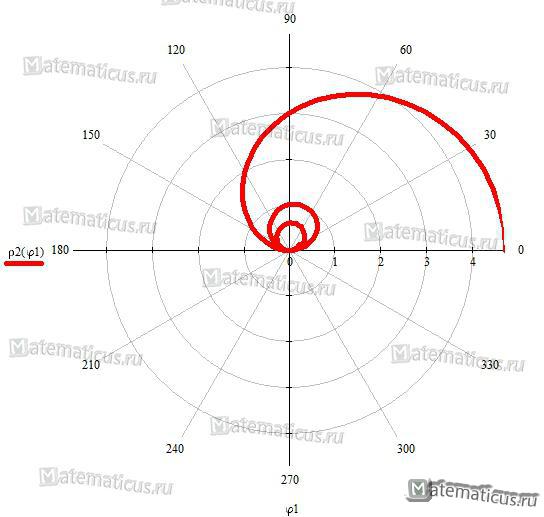
Логарифмическая спираль
Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:
Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

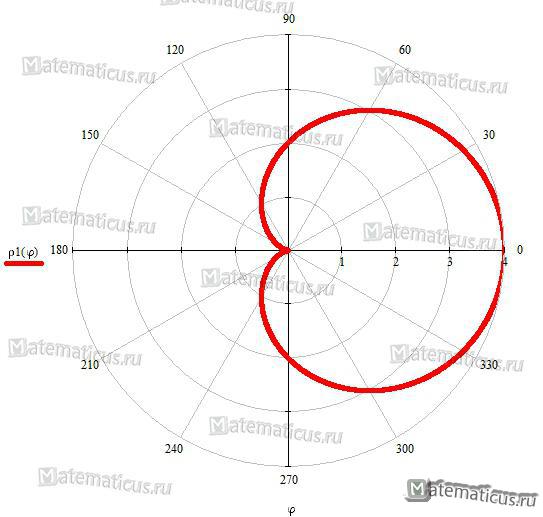
Кардиоида
Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Астроида
Уравнение астроиды (перев. греч. звезда и вид) :
x 2/3 + y 2/3 = a 2/3
Видео:Видеоурок "Полярная система координат"Скачать

Строфоида
Уравнение строфоиды (перев. греч. крученая лента, поворот) :
y 2 (a — x)= x 2 (a + x)
Уравнение строфоиды в полярной системе координат:
Видео:Полярная система координатСкачать

Видео:Построение кривой в полярной системе координатСкачать

Декартов лист
Уравнение декартова листа :
x 2 + y 2 — 3axy = 0
Уравнение декартова листа в полярной системе координат:
Видео:Полярная система координатСкачать

Циссоида
Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :
Параметрическое уравнение циссоиды:
x = a t 2 /(1 + t 2 )
x = a t 3 /(1 + t 2 )
Уравнение циссоиды в полярной системе координат:
Видео:Астроида: найдем площадь и длину через определенный интегралСкачать

Циклоида
Параметрическое уравнение циклоиды :
Видео:Декартовы координатыСкачать

Кохлеоида
Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:
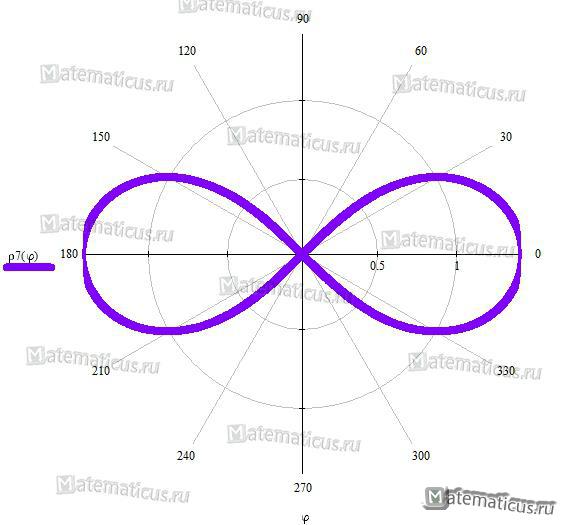
Лемниската Бернулли
Уравнение лемниската Бернулли в прямоугольных координатах:
(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )
Уравнение лемниската Бернулли в полярных координатах:
Архимедова спираль рассмотрена здесь подробно.
Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.
Видео:1636. Площадь криволинейной трапеции в декартовой системе координат.Скачать

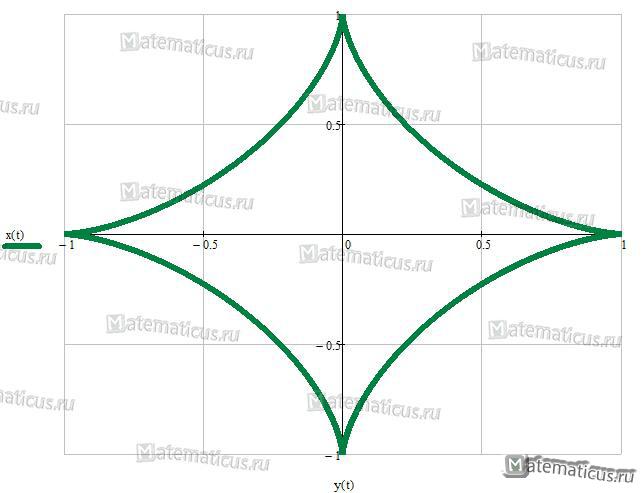
Уравнения кривых. Астроида.
Астроида – плоская кривая, которую формирует траектория точки, расположенной на окружности радиуса r, катящейся без трения по внутренней стороне неподвижной окружности радиуса R = 4r.
Параметрическое уравнение:
Уравнение в алгебраическом виде:
Длина дуги от точки с 0 до t ≤ π/2:
.
Длина всей кривой равна 6R.
Радиус кривизны описывается формулой:
.
Площадь, ограниченная кривой представлена такой формулой:
.
Объем тела вращения относительно любой координатной оси описан формулой:
.
Видео:1693 Длина астроидыСкачать

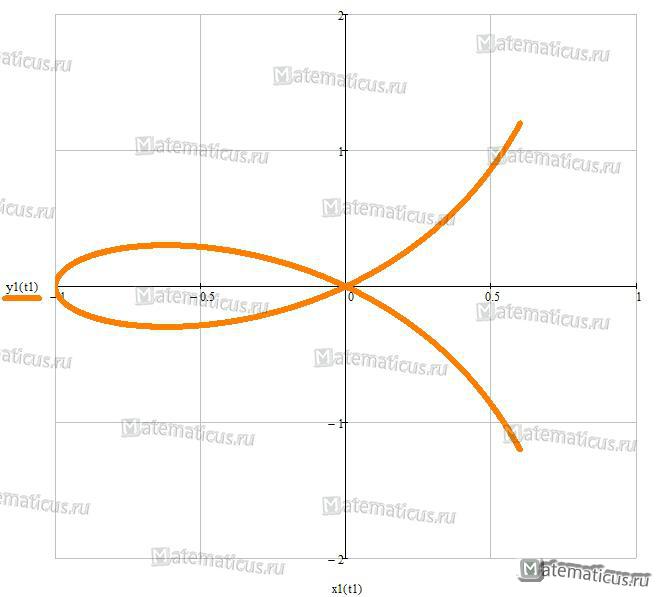
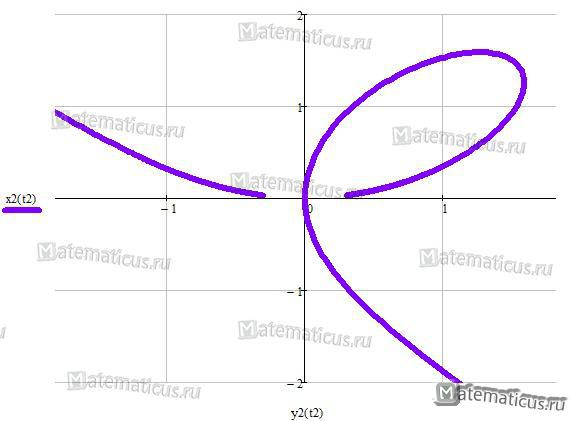
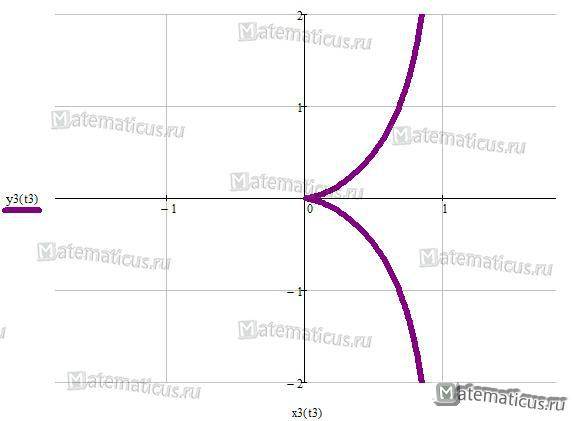
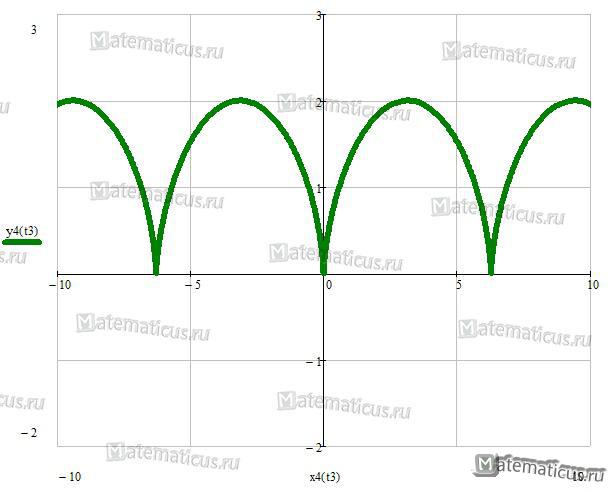
Графики функций, заданных параметрически:
Видео:Модель декартовой системы координат.Скачать

Астроида (звездообразная кривая)
Астроид — это старое название астероидов, небесных тел, вращающихся вокруг Солнца, по размеру много меньше размеров планет.
При наблюдении в телескоп они выглядят как звезды.
Кривая астроид по форме напоминает звезду на ночном небе, поэтому и получила такое название.
Впервые данную кривую «астроидом» назвал астроном Карл Людвиг Литров в своей книге, опубликованной в 1836 году в Вене. До этого времени кривая называлась кубоциклоид.
Исследованием данной кривой также занимались известные ученые: Рёмер, Бернулли, Лейбниц, д’Аламбер.
📺 Видео
Кривые, заданные параметрическиСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

1642 Площадь астроидыСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Декартовые координаты на плоскости. Алгеба 8 класс. Урок 1Скачать