Разделы: Математика
Тема тригонометрических уравнений начинается со школьной лекции, которая строится в виде эвристической беседы. На лекции рассматривается теоретический материал и образцы решения всех типовых задач по плану:
- Простейшие тригонометрические уравнения.
- Основные методы решения тригонометрических уравнений.
- Однородные уравнения.
На следующих уроках начинается самостоятельная отработка навыков, основанная на применении принципа совместной деятельности учителя и ученика. Сначала устанавливаются цели для учащихся, т.е. определяется, кто хочет знать не более того, что требуется государственным стандартом, а кто готов заниматься больше.
Итоговая диагностика создается с учетом уровневой дифференциации, что позволяет учащимся осознанно определять тот минимум знаний, который необходим для получения оценки “3”. Исходя из этого, отбираются разноуровневые материалы для диагностики знаний учащихся. Такая работа позволяет осуществить индивидуальный подход к учащимся, включить каждого в осознанную учебную деятельность, формировать навыки самоорганизованности и самообучения, обеспечивать переход к активному, самостоятельному мышлению.
Семинар проводится после отработки основных навыков решения тригонометрических уравнений. За несколько уроков до семинара ученикам даются вопросы, которые будут рассматриваться на нем.
Семинар состоит из трех частей.
1. Во вводной части рассматривается весь теоретический материал, включая знакомство с проблемами, которые возникнут при решении сложных уравнений.
2. Во второй части рассматриваются решение уравнений вида:
- а cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- уравнения, решаемые через понижение степени.
В этих уравнениях применяются универсальная подстановка, формулы понижения степени, метод вспомогательного аргумента.
3. В третьей части рассматриваются проблемы потери корней и приобретение посторонних корней. Показывается, как надо отбирать корни.
Ученики работают в группах. Для решения примеров вызываются хорошо подготовленные ребята, которые могут показать и объяснить материал.
Семинар рассчитан на хорошо подготовленного ученика, т.к. на нем рассматриваются вопросы несколько выходящие за рамки программного материала. В него включены уравнения более сложного вида, и особо рассматриваются проблемы, возникающие при решении сложных тригонометрических уравнений.
Семинар проводился для учеников 10 – 11 классов. Каждый ученик получил возможность расширить и углубить свои знания по этой теме, сравнить уровень своих знаний не только с требованиями, предъявляемыми к выпускнику школы, но и с требованиями предъявляемыми поступающим в В.У.З.
СЕМИНАР
Тема: «Решение тригонометрических уравнений»
Цели:
- Обобщить знания по решению тригонометрических уравнений всех типов.
- Заострить внимание на проблемах: потеря корней; посторонние корни; отбор корней.
- I. Вводная часть
- II. Примеры тригонометрических уравнений
- III. Проблемы возникающие при решении тригонометрических уравнений
- Основные методы решения тригонометрических уравнений
- п.1. Разложение на множители
- п.2. Приведение к квадратному уравнению
- п.3. Приведению к однородному уравнению
- п.4. Введение вспомогательного угла
- п.5. Преобразование суммы тригонометрических функций в произведение
- п.6. Преобразование произведения тригонометрических функций в сумму
- п.7. Понижение степени
- п.8. Замена переменных
- п.9. Использование ограничений области значений функций
- п.10. Примеры
- Простейшие тригонометрические уравнения
- 🎥 Видео
I. Вводная часть
1. Основные методы решения тригонометрических уравнений
- Разложение на множители.
- Введение новой переменной.
- Функционально-графический метод.
2. Некоторые типы тригонометрических уравнений.
- Уравнения, сводящиеся к квадратным уравнениям, относительно cos х = t, sin х = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Вsinx + C = 0.
Решаются методом введения новой переменной.
- Однородные уравнения первой и второй степени
Уравнение первой степени: Asinx + Bcosx = 0 разделим на cos x, получим Atg x + B = 0
Уравнение второй степени: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 разделим на cos 2 x, получим Atg 2 x + Btgx + C = 0
Решаются методом разложения на множители и методом введения новой переменной.
- Уравнение вида: Аsinx + Bcosx = C. А, В, С
0
- Понижение степени:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Решаются методом разложения на множители.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Сводятся к однородным: С = С(sin 2 х + cos 2 х).
- Сводятся к уравнению: Аsin2x + Bcos2x = C.
- Уравнение вида: A(sinx + cosx) + Bsin2x + C = 0.
Сводятся к квадратным относительно t = sinx + cosx; sin2x = t 2 – 1.
3. Формулы.
- Универсальная подстановка:
х

+ 2
n; Проверка обязательна!
- Понижение степени: cos 2 x = (1 + cos2x): 2; sin 2 x = (1 – cos 2x): 2
- Метод вспомогательного аргумента.
Acosx + Bsinx заменим на Csin (x +
), где
sin
= а/С; cos
= в/С;

4. Правила.
- Увидел квадрат – понижай степень.
- Увидел произведение – делай сумму.
- Увидел сумму – делай произведение.
5. Потеря корней, лишние корни.
- Потеря корней: делим на g(х); опасные формулы (универсальная подстановка). Этими операциями сужаем область определения.
- Лишние корни: возводим в четную степень; умножаем на g(х) (избавляемся от знаменателя). Этими операциями расширяем область определения.
II. Примеры тригонометрических уравнений
1. Уравнения вида Asinx + Bcosx = C
1)Универсальная подстановка.О.Д.З. х – любое.
3 sin 2x + cos 2x + 1= 0.
tgx = u. х 


tg x = –1/3, x = arctg (–1/3) + 

Проверка: 3sin( 





х = 

Ответ: х = arctg(–1/3) + 




2)Функционально-графический метод. О.Д.З. х – любое.
Sinx – cosx = 1
Sinx = cosx + 1.
Построим графики функций: y = sinx, y = cosx + 1.
Ответ: х = 






3) Введение вспомогательного аргумента. О.Д.З.: х – любое.
8cosx + 15 sinx = 17.
8/17 cosx + 15/17 sinx = 1, т.к. (8/17) 2 + (15/17) 2 = 1, то существует такое 

cos 



sin (x + 
Ответ: x = 





2. Понижение порядка: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). sin 2 3x + sin 2 4x + sin 2 6x + sin 2 7x = 2. О.Д.З.: х – любое.
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x(cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Ответ: х = 








| При | k = 1 и m = 0 k = 4 и m = 1. | серии совпадают. |
3. Сведение к однородному. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 
5 sin 2 х + 

cos 2 х = 0 удовлетворяет уравнению.
cosx ( 
cosx = 0, 
х = 






Ответ: х = 





4. Уравнение вида: А(sinx + cosx) + В sin2x + С = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. О.Д.З.: х – любое.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | 2 – 5t + 2 = 0. t1 = 2, t2 = Ѕ.
sinx + cosx = Ѕ. cosx = sin(x + 
sinx +sin(x + 
2sin(x + 

sin(x + 

x +


Ответ: х = (–1) k arcsin(1/2



5. Разложение на множители.
1) cos 2 х – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1) сosx = 2, корней нет.
2) сosx + 2 sinx = 0
2tgx + 1 = 0
Ответ: x = arctg(1/2) + 

III. Проблемы возникающие при решении тригонометрических уравнений
1. Потеря корней: делим на g(х); применяем опасные формулы.
1) Найдите ошибку.
1 – сosx = sinx *sinx/2,
1 – сosx = 2sin 2 х/2 формула.
2 sin 2 х/2 = 2 sinx/2* сosx/2* sinx /2 разделим на 2 sin 2 х/2,
1 = сosx/2
х/2 = 2 


Потеряли корни sinx/2 = 0, х = 2

Правильное решение: 2sin 2 х/2(1 – сosx /2) = 0.
| sin 2 х/2 = 0 x = 2  k, k k, k  Z. Z. | 1 – сosx /2 = 0 x = 4p n, n  Z. Z. |
2. Посторонние корни: освобождаемся от знаменателя; возводим в четную степень.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 

2сos3х sinx – сos3x + 2sinx – 1 = 0
(сos3x + 1)(2sinx – 1) = 0
| 1). сos3x + 1 = 0 х =  /3 + 2 /3 + 2 n/3, n n/3, n  Z. Z. | 2). 2sinx – 1 = 0 x = (–1) k  /6 + /6 +  k, k k, k  Z. Z. |
I. х =  /3 + 2 /3 + 2 n/3 n/3 1. n = 0 sin 2  /3 = /3 =  3 / 2 3 / 2 не удовлетворяют. О.Д.З. 2. n = 1 3. n = 2 | II. x = (–1) k  /6 + /6 +  k, k k, k  Z Z 1. k = 0 sin 2  /6 = /6 =  3 / 2 3 / 2 не удовлетворяют О.Д.З. 2. k = 1 sin 2*5  /6 = – /6 = – 3 / 2 3 / 2 удовлетворяют О.Д.З. |
Ответ: х = 






2). 

1 – sin t = 2 cos 2 t
| 1). sin t = –1, t = –  /2 + 2 /2 + 2  k, k k, k  Z; Z; | 2). sin t = 1/2, t = (–1) n  /6 + /6 +  n, n n, n  Z; Z; |
I. t = –  /2 + 2 /2 + 2  k, k k, k  Z; Z; 1. k = 0 t = –  /2 /2 удовлетворяют О.Д.З. | II. t = (–1) n  /6 + /6 +  n, n n, n  Z; Z; 1. n = 0 t =  /6 /6 удовлетворяют О.Д.З. 2. n = 1 t = 5  /6 /6 не удовлетворяют О.Д.З. |
| Ответ: t = –  /2 + 2 /2 + 2  k, k, x = –  /4 + /4 +  k, k, k  Z, Z, | t =  /6 + 2 /6 + 2  n, n, x =  /12 + /12 +  n, n, n  Z. Z. |
3. Отбор корней.
1). tgx + tg2x = tg3x О.Д.З.: х 






| sin3x sinx sin2x = 0 sin3x = 0 x =  n/3, n n/3, n  Z, Z,n = 0, x = 0 уд. | sinx = 0 x =  h, h h, h  Z, Z,h = 0, x = 0 уд. | sin2x = 0 x =  m/2, m m/2, m  Z. Z.m = 0, x = 0 уд. Ответ: x = Видео:Решение уравнения вида a sin x + b cos x = cСкачать  Основные методы решения тригонометрических уравненийп.1. Разложение на множителиАлгоритм простого разложения на множители Шаг 1. Представить уравнение в виде произведения (f_1(x)cdot f_2(x)cdot . cdot f_n(x)=0) где (f_i(x)) — некоторые функции (тригонометрические и не только) от (x). Например:
Возможно, у вас не сразу получится объединять решения, которые частично пересекаются или дополняют друг друга. Алгоритм разложения на множители со знаменателем Шаг 1. Представить уравнение в виде произведения $$ frac=0 $$ где (f_i(x), g_i(x)) — некоторые функции (тригонометрические и не только) от (x). Например:
За счет требования (xnefrac) исключаются семейства (x=fracpi2+2pi k) и (x=2pi k). п.2. Приведение к квадратному уравнениюШаг 1. С помощью базовых тригонометрических отношений и других преобразований представить уравнение в виде $$ af^2(x)+bf(x)+c=0 $$ где (f(x)) — тригонометрическая функция. Например: п.3. Приведению к однородному уравнениюАлгоритм решения однородного тригонометрического уравнения 1-й степени Например: Алгоритм решения однородного тригонометрического уравнения 2-й степени Шаг 1. Разделить левую и правую части уравнения на (cos^2x) begin frac=frac\ Atg^2x+Btgx+C=0 end Шаг 2. Сделать замену переменных: (t=tgx). Решить полученное квадратное уравнение: begin at^2+bt+c=0\ D=b^2-4ac, t_=frac<-bpmsqrt> end Шаг 3. Решить совокупность простейших тригонометрических уравнений ( left[ begin tgx=t_1\ tgx=t_2 end right. ) Например: Обобщим понятие однородного тригонометрического уравнения на любую натуральную степень: Алгоритм решения однородного тригонометрического уравнения n-й степени Шаг 1. Разделить левую и правую части уравнения на (cos^n x) Например: п.4. Введение вспомогательного углаНапример: п.5. Преобразование суммы тригонометрических функций в произведениеПри решении уравнений вида begin Asinax+Bsinbx+. +Ccoscx+Dcosdx+. =0 end используются формулы, выведенные в §17 данного справочника. Например:
п.6. Преобразование произведения тригонометрических функций в суммуПри решении уравнений вида begin sinaxcdot cosbx=sincxcdot cosdx, sinaxcdot sinbx=sincxcdot cosdx text end используются формулы, выведенные в §18 данного справочника. Например:
Примечание: учитывая ответ предыдущего примера, это же множество решений можно записать в виде: ( left[ begin x=frac\ x=pmfracpi6+pi k end right. Leftrightarrow left[ begin x=fracpi6+frac\ x=pi k end right. ) п.7. Понижение степениПри решении уравнений вида begin sin^2ax+sin^2bx+. +cos^2cx+cos^2dx+. =A end используются формулы понижения степени: begin sin^2x=frac, cos^2x=frac end (см. формулы половинного аргумента, §15 данного справочника). Например:
п.8. Замена переменныхПри решении уравнений вида (f(sinxpm cosx, sinxcosx)=0) используется замена begin t=cosxpm sinx end Например: п.9. Использование ограничений области значений функцийУравнения вида begin underbrace_<m text> end может иметь решение только, если каждое из слагаемых равно 1. Аналогично, уравнение вида begin underbrace_<m text> end может иметь решение только, если каждое из слагаемых равно -1. Например:
п.10. ПримерыПример 1. Используя различные методы, решите уравнения: б) (6sinxcosx=5cos2x) в) (9cos^2x-5sin2x=-sin^2x) г) (cos3x-1=cos6x) д) (sqrtsin2x-cos2x=-sqrt) е) (cos^2x+cos^2 2x=cos^2 3x+cos^2 4x) Пример 2*. Решите уравнения: б) (frac+1=7frac)
2) Решаем для отрицательного косинуса (2-я и 3-я четверти) begin frac+1=-7frac\ 3(1+tg^2x)+1+7tgx=0\ 3tg^2x+7tgx+4=0\ (3tgx+4)(tgx+1)=0\ left[ begin tgx=-frac43\ tgx=-1 end right. Rightarrow left[ begin x=-arctgfrac43+pi k\ x=-fracpi4+pi k end right. end
3) Объединяем полученные решения: begin left[ begin x=arctgfrac43+2pi k\ x=fracpi4+2pi k\ x=pi-arctgfrac43+2pi k\ x=frac+2pi k end right. end
Окончательно получаем: ( left[ begin x=(-1)^k arctgfrac43+pi k\ x=(-1)^k fracpi4+pi k end right. ). г) (3sinx-4cosx=5) Способ 2. Делаем универсальную подстановку: begin sinalpha=frac<2tgfrac>, cosalpha=frac\ 3cdot frac<2tgfrac><1+tg^2frac>-4cdotfrac<1-tg^2frac><1+tg^2frac>=5\ frac<6tgfrac-4left(1-tg^2fracright)-5left(1+tg^2fracright)><1+tg^2frac>=0 end (1=tg^2fracgeq 1), знаменатель никогда не превращается в 0, отбрасываем его и работаем с числителем: begin -tg^2frac+6tgfrac-9=0Rightarrow tg^2frac-6tgfrac+9=0Rightarrowleft(tgfrac-3right)^2=0Rightarrow tgfrac=3\ frac=arctg3+pi kRightarrow x= 2arctg3+2pi k end Докажем, что полученные ответы: $$ x=-arcsinfrac35+pi+2pi k text x=2arctg3+2pi k $$ равнозначны, т.е. (-arcsinfrac35+pi=2arctg3), и равны углы: $$ arcsinfrac35=pi-2arctg3 (*) $$ Пусть в правой части равенства (*) (2arctg3=varphi). Тогда (arctg3=fracvarphi2) и (tgfracvarphi2=3). Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать  Простейшие тригонометрические уравненияУравнение sinx = a, x- неизвестная переменная, a – некоторое постоянное число. а) Если a>1 или a n arcsina+πn, n Например, решение уравнения sinx = 0,3 записывается в виде: x = (-1) n arcsin0,3+πn, n Уравнение соsx = a, x- неизвестная переменная, a – некоторое постоянное число. а) Если a>1 или a б)Ecли a = 1, то решение уравнения: x= в) Ecли a= -1, то решение уравнения: x= г) Ecли a= 0, то решение уравнения: x= д) Ecли a Например, решение уравнения cosx = 0,3 записывается в виде x= Уравнение tgx = a, x – неизвестная переменная, a – некоторое постоянное число. Решение уравнения x = arctga + πn, n Например, решение уравнения tgx =3, будет x = arctg3 + πn, n Замечание: если a = 0, то x = πn, n Схема решения простейших тригонометрических уравнений Нет корней
а) sinx = 3; б) sinx = — а) Так как 3>1, то решений нет. Ответ: решений нет. б) x =(-1) k arcsin(- x =(-1) k +1 в) Так как -2,3>1, то решений нет; Ответ: решений нет. г) x= Ответ: д) tgx = 3.Виды тригонометрических уравнений: 1.Уравнения, в которых можно выполнить замену переменной Такие тригонометрические уравнения можно привести, например, к виду где a,b,c – некоторые действительные числа,a ≠0, f(x)- одна из тригонометрических функций. Например, 4sin 2 x +5 sinx+1 = 0. Обозначим sinx = t, (1)тогда данное уравнение можно записать в виде: 4t 2 +5t +1 = 0, это квадратное уравнение относительно t, найдем его корни. Подставим найденные значения t1 и t2 в равенство (1). Получим простейшие тригонометричкские уравнения sinx =-1,sinx =- 0,25. Решение первого уравнения x= — x =(-1) k+1 arcsin0,25+ Ответ: — Решить уравнение sin 2 x + cosx +1= 0. sin 2 x + cosx +1= 0, заменяя sin 2 x = 1- cos 2 x, получим 1- cos 2 x+ cosx +1= 0, cos 2 x — cosx -2= 0. Обозначим cosx = t, (1)тогда данное уравнение можно записать в виде: t 2 -t -2 = 0, это квадратное уравнение относительно t найдем его корни. Подставим найденные значения t1 и t2 в равенство (1). Получим простейшие тригонометричкские уравнения cosx = -1, cosx = 2. Решение первого уравнения x= Второе уравнение решений не имеет, т.к. 2>1. Ответ: 2.Однородные тригонометрические уравнения. Такие уравнения можно привести к виду a∙sin 2 x+bsinxcosx+ k∙cos 2 x= 0, a,b,k – некоторые действительные числа, a≠0, k≠0. Например, 4sin 2 x +5sinx cosx+cos 2 x = 0.Такие уравнения – однородные уравнения второй степени Чтобы решить такое уравнение, надо: 1. Разделить почленно обе части уравнения на cos 2 x ≠ 0,т.е. 4 2.Выполнить преобразования: 4 3.Решить квадратное уравнение относительно tgx, tgx =t. tgx = -1, tgx = — 0,25. x = arctg(-1)+πk, x = — Ответ: — Решить уравнение 4sin 2 x +sin2x -3 = 0. Заменим в данном уравнении sin2x по формуле двойного аргумента на 2sinxcosx, а 3- на 3sin 2 x +3сos 2 x , т.к. sin 2 x +сos 2 x =1, получим: 4sin 2 x +2sinxcosx-3sin 2 x -3сos 2 x =0, sin 2 x +2sinxcosx-3сos 2 x =0. Последнее уравнение – однородное. Решим его: 1. 2. 3. tgx =t, t 2 +2t — 3= 0. D=16, t1= 1;t2= -2 . x = arctg1+πk, x = Ответ: Для решения однородных уравнений можно использовать следующую таблицу:
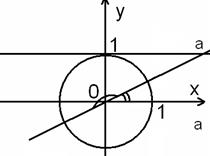
3.Уравнение вида asinx+bcosx=c Чтобы решить уравнение такого вида (например,3sinx+4cosx=2), можно 1.Записать его в виде sin(x +t) = sin(x +t) = 2.Решить простейшее тригонометрическое уравнение: sin(x +t) = ( в нашем случае sin(x +t) = x = (-1) k arcsin0,4 – t +πk, 3. Определить t, t = arctgb/a ( в нашем случае t = arctg4/3); 4. Записать ответ: x = (-1) k arcsin0,4 – arctg4/3+πk, Решите уравнение 2sinx +cosx = 1. 1. sin(x +t) = 2. x+t = (-1) k arcsin 4. Для решения уравнения вида
Если левая часть тригонометрического уравнения Для решения тригонометрических уравнений данным способом можно использовать таблицу 5.Некоторые другие виды тригонометрических уравнений а) sin(3x+ а) sin(3x+ Обозначим 3x+ Решим это уравнение относительно х: 3x = — Ответ: — б) sin2x – cosx = 0. Заменим в данном уравнении sin2x по формуле синуса двойного аргумента на 2sinxcosx, получим 2sinxсos + cosx = 0. Затем вынесем cosx за скобки, получим: cosx (2sinx-1) = 0, откуда сosx = 0 или 2sinx -1=0; x = x = Ответ: в) sinx + cosx = 0. Это уравнение можно рассматривать как однородное уравнение первой степени относительно функций синуса и косинуса. Чтобы решить это уравнение : Разделим почленно обе части уравнения на cosx,получим: tgx +1 = 0, tgx = -1 . 3.Решим простейшее уравнение tgx = -1, x= Ответ: 6.Уравнения, решаемые с помощью применения свойств ограниченности тригонометрических функций
Ответ: 2) Ответ: 🎥 ВидеоУравнение вида a sin x + b cos x =cСкачать  Уравнения вида a*sinx+b*cosx=cСкачать  10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать  Решение биквадратных уравнений. 8 класс.Скачать  10 класс, 30 урок, Преобразование выражения Asinx + Bcosx к виду Csin(x+t)Скачать  Решение тригонометрических уравнений. 10 класс.Скачать  Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать  Решение тригонометрических уравнений и их систем. 10 класс.Скачать  Решение уравнения a*sin^2(x)+b*sin(x)*cos(x)+c*cos^2(x)=0Скачать 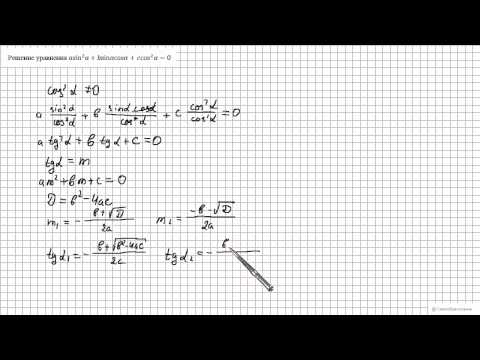 Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать  Решите уравнение ➜ sinx+cosx=1 ➜ 2 способа решенияСкачать  ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ решение примеров 10 классСкачать  Решение тригонометрических уравнений. Метод понижения порядка. 10 класс.Скачать  Тригонометрия. Уравнения. Метод введения вспомогательного угла для уравнений вида asinx+bcosx=c.Скачать  Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать  Преобразование выражения A sin x + В cos x к виду С sin (х + t) | Алгебра 10 класс #38 | ИнфоурокСкачать  КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать  |
 0
0
 sin
sin 














 .
.



 то x=
то x=  arccosa+2πn, n
arccosa+2πn, n 

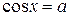
 Нет корней
Нет корней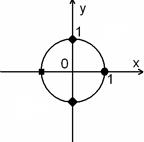

 ■
■ 
 ■
■ ♦
♦ 
 ♦
♦ ●
● 
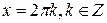 ●
●









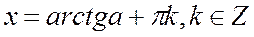

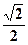 ; в) cosx = -2,3; г) cosx = —
; в) cosx = -2,3; г) cosx = —  .
. x =(-1) k
x =(-1) k 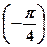 +
+ 
 +
+  , x=
, x=  ;
; +
+  Решение второго уравнения
Решение второго уравнения ; (-1) k+1 arcsin0,25+
; (-1) k+1 arcsin0,25+  ,
, ;
; 4tg 2 x +5tgx+1=0.
4tg 2 x +5tgx+1=0. или x = arctg(-0,25)+πn,
или x = arctg(-0,25)+πn,  ,
, ;
; tg2x +2tgx — 3= 0.
tg2x +2tgx — 3= 0. 2. Решить уравнение
2. Решить уравнение 
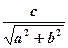 ( в нашем случае sin(x +t) =
( в нашем случае sin(x +t) =  ,
, ).
). , sin(x +t) =
, sin(x +t) =  ;
; , где
, где  можно использовать следующую таблицу:
можно использовать следующую таблицу:
 ,
,  ,
,  .
. содержит лишь одно из выражений
содержит лишь одно из выражений  или
или  и функцию
и функцию 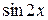 (или произведение
(или произведение  ), то, вводя новую переменную
), то, вводя новую переменную  или
или  и учитывая, что
и учитывая, что  ,
,  , приходим к уравнению относительно
, приходим к уравнению относительно 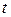 .
.
 +
+  , разделим все члены правой части уравнения на 3, получим x = —
, разделим все члены правой части уравнения на 3, получим x = —  + (-1)k
+ (-1)k  +
+  .
. или sinx = 0,5;
или sinx = 0,5;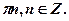



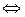

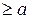

 . Так как
. Так как  и
и  для
для  , то уравнение
, то уравнение 

 Так как
Так как  , то
, то  — корень исходного уравнения.
— корень исходного уравнения.