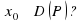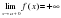Как и обещал продолжаю тему «Программы, которые помогают решать математику. ». И сегодня расскажу о программе Advanced Grapher, с помощью которой легко можно построить график практически любой функции.
Посмотрев эти видеоуроки вы узнаете как можно легко построить график:
- обычной функции;
- функции в полярной системе координат;
- заданный параметрическим уравнением;
- касательной или нормали;
- неравенства;
- производной;
- любой части плоскости;
- и многое другое.
Также вы можете скачать программу для построения графиков Advanced Grapher нажав по ссылке: скачать Advanced Grapher .
Или можете просто посмотреть видео-уроки по данной теме ниже:
Видеоурок часть 1:
Видеоурок часть 2:
Видео:Построение графиков Advanced Grapher.Скачать

Асимптоты графика функции. Нахождение асимптот.
Методическая разработка занятия дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот» по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям) выполнена в соответствии с рабочей программой.
Организация-разработчик: ГОУ СПО ЛНР «Луганский строительный колледж».
Разработчик: Еськова Лариса Викторовна, преподаватель – методист высшей квалификационной категории.
Аннотация: данная методическая разработка помогает в доступной форме с использованием компьютерных технологий обучения ознакомить студентов с понятием асимптоты графика функции, видами асимптот и методами их нахождения. Использование графического редактора позволяет наглядно продемонстрировать правильность найденного решения или же найти допущенную ошибку.
Формы организации познавательной деятельности:
*метод коллективного взаимодействия;
*метод контроля и оценки
Просмотр содержимого документа
«Асимптоты графика функции. Нахождение асимптот.»
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Луганский строительный колледж»
занятия по дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот»
специальностm 38.02.01 «Экономика и бухгалтерский учёт (по отраслям)».
категории Еськова Л.В.
Познакомить с определением асимптоты графика функции, видами асимптот и методами их нахождения, обобщить и систематизировать знания определения предела функции и закрепить умения нахождения пределов функции;
Развивать аналитическое мышление, умение проводить аналогии, сравнивать и обобщать;
Воспитывать аккуратность, графическую культуру, усидчивость и настойчивость в достижении результата.
Материально-техническое обеспечение и дидактические средства, ТСО: доска, ПК, мультимедийная установка, программное обеспечение (Windows 7, Advanced Grapher), раздаточный материал.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах)Т.2. Дифференциальное и интегральное исчисление. М., Дрофа, 2004. – 512 с.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах) Т.3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного пер еменного. М., Дрофа, 2004. — 512 с.
Грибанов В.М., Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I, II, III).-Луганск: Изд-во ВНУ им. В.Даля, 2003.
Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. – Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. — 100 стр. Методические указания по курсу высшей математики. Часть 1.
Роева Т.Г., Хроленко Н.Ф. Алгебра в таблицах, 10-11 класс: Учеб. пособие.- Х.: Издательская группа «Академия».
Приветствие. Сообщение темы и цели занятия.
Мотивация учебной деятельности.
Сегодня на занятии мы знакомимся с очень важным понятием математического анализа асимптотами графика функции. Вы уже умеете проводить исследование функции и построение графика с помощью производной, находить промежутка монотонности, экстремумы функции и промежутки выпуклости и вогнутости, точки перегиба. Но как ведет себя функция в точках разрыва, как построить ее график вблизи этих точек. Ответы на эти и другие вопросы мы должны узнать на этом занятии. Итак запишите в тетради план занятия:
Асимптоты графика функции.
Использование программного обеспечения для построения асимптот.
Нахождение асимптот графиков функции.
2. Актуализация опорных знаний.
Так как нахождение асимптот напрямую связано с вычислением пределов функции, то давайте повторим основные правила нахождения пределов.
Как найти предел многочлена 
Как найти предел дробно — рациональной функции: 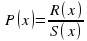
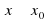
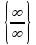
Как избавиться от неопределенности 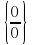
Назовите первый замечательный предел.
Изложение нового материала.
При исследовании графика функции при 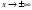
Если график функции 
Определение Прямая L называется асимптотой графика функции 
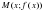
Определение. Прямая 

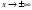
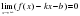
Существует три вида асимптот: горизонтальные, вертикальные и наклонные.
Вертикальная асимптота 
Определение. Прямая 



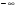
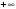
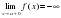
Очевидно, прямая 






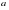
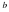
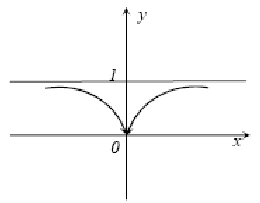
Горизонтальная асимптота 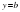
Определение. Прямая 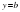


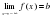
Если конечен только один из пределов 
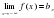


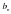
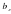
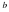
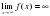
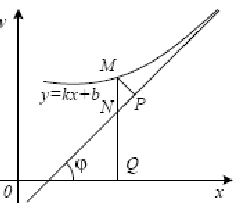
Наклонная асимптота
Определение. Прямая 

Если, хотя бы один из пределов не существует или равен бесконечности, то график исследуемой функции не имеет соответствующей наклонной асимптоты.
Использование программного обеспечения Advanced Grapher к построению асимптот графика функции.
Advanced Grapher является мощным программным графическим обеспечением. Вы можете использовать его для построения графиков функций, уравнений, неравенств и таблиц.
Программа также позволяет выполнять построение кривых, анализировать
Видео:Регрессионный анализ Advanced Grapher или как построить функцию зависимости по нескольким точкамСкачать

Исследование функций в программе Advanced Grapher на уроках алгебры в старших классах
статья по алгебре (10 класс) по теме
В статье подробно рассказано, как используя программу Advanced Grapher можно строить графики алгебраических и тригонометрических функций в декартовой системе координат, исследовать функции, находить производную, первообразную, вычислять площади замкнутых фигур. Приведены примеры решения типичных задач на уроке алгебры в старших классах и показаны преимущества программы при исследованиях функции.
Видео:Advanced Grapher - программа для построения графиковСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Statya.docx | 406.19 КБ |
Видео:Математический анализ, 15 урок, АссимптотыСкачать

Предварительный просмотр:
ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ Advanced Grapher НА УРОКАХ АЛГЕБРЫ В СТАРШИХ КЛАССАХ
МОУ – СОШ № 3 (г. Можайск Московской обл.)
В статье подробно рассказано, как используя программу Advanced Grapher можно строить графики алгебраических и тригонометрических функций в декартовой системе координат, исследовать функции, находить производную, первообразную, вычислять площади замкнутых фигур. Приведены примеры решения типичных задач на уроке алгебры в старших классах и показаны преимущества программы при исследованиях функции.
Ключевые слова: программа Advanced Grapher, графики, исследование функций.
Учитель, располагающий компьютером, имеет уникальную возможность сделать процесс обучения более наглядным и динамичным с помощью графической программы Advanced Grapher, которая обладает огромным количеством возможностей, в том числе, позволяет строить графики в полярной системе координат, а также линии, заданные параметрически, что упрощает работу ученика при построении графиков.
Рассмотрим особенности использования программы Advanced Grapher на уроке алгебры в старших классах.
1. Закрепить умение строить графики в различных системах координат.
2. Закрепить знания школьного алгоритмического языка.
3. Закрепить математические знания по теме: “Исследования функции”.
4. Развивать внимательность, логику мышления.
Тип урока : интегрированный.
- усвоение учащимися понятий алгоритмического языка, математического языка, знание темы исследование функции;
- формирование у учащихся умений и навыков работы с программой Advanced Grapher;
- развивать умение считывать информацию и пользоваться ею;
- развитие познавательного интереса учащихся;
- развитие у учеников логического мышления, памяти, внимания;
- формирование информационной культуры учащихся;
- воспитание трудолюбия;
- прививание учащимся навыков самостоятельной работы.
а) вспомнить ключевые слова из школьного алгоритмического языка:
— абсолютная величина: abs ;
— запись тригонометрический функций: sin ( x ), cos ( x ) и т.д.;
— степень 2 x , 2^ x , sin 2 x – ( sin ( x ))^2.
II. Работа в классе:
№ 1. Исследовать функцию y = ( x 2 – 1)/ x , построив её график [1].
Используя график построенной функции определим:
1. Область определения.
2. Монотонность функции (т.е. промежутки возрастания или убывания
3. Промежутки знакопостоянства:
4. Чётность или нечётность, т.е. f (- x ) = f ( x ) — симметрично относительно
оси координат; f (- x ) = — f ( x ) — симметрично относительно начала координат.
5. Нули функции (точки пересечения графика):
6. Точки экстремума: max y = [ ]; min y = [ ].
Каждый учитель и ученик знает, как однообразны и трудоёмки уроки исследования функций, как порой нелегко объяснить некоторые этапы исследования: особенности окрестности точки, в которых происходит перегиб; асимптоты графика и другие. Данная программа облегчает объяснение материала, а ученикам позволяет быстрее усвоить трудные места этого материала, поскольку дает возможность увеличить размеры графика, выполнить дополнительные построения, более детально и полно производить исследование функции.
Выполнение работы в программе Advanced Grapher
1) График→Добавить график→Свойства y ( x )→(вносим формулу ( x ^2 – 1)/ x )) (рис. 1). Полученный график представлен на рис. 2.
2) Вычисления→Исследования функции→(вносим функцию целиком) →Нули функции + экстремумы функции + min + max (+ использование производной) (рис. 3).
3) Результат исследования (по производной):
б) экстремумы (рис. 4).
4) Результат исследования без производной:
5) Вычисления→Пересечения→ y ( x 1 ) = ( x ^2 – 1)/ x ;
6) Касательная y ( x ) = ( x ^2 – 1)/ x, точка касания x = -1.
Касательная→Добавить график→Свойства→ OK (формула).
Результат решения показан на рис. 5.
График любой функции можно построить и по точкам, т.е. по таблице.
Таблица значений→формула ( x ^2 – 1)/ x от -10 до 10 с шагом 1 →Вычисления функции→ формула ( x ^2 – 1)/ x →Считать.
Мы рассмотрели подробно пример решения №1, так же были исследованы и построены графики функций примеров №2 — №4.
№2. Построить график функции: y = ׀2 x + 3׀ +3׀ x -1׀ – ׀ x +2׀.
№3. Построить график функции: y = 2 x · cosx .
(Графики→Наборы свойств→Тригонометрический набор
y ( x ) = 2^ x * cos ( x )) → OK →Получаем график.
№4. Построить графики функций: (не на одном)
а) y = 1 + sinx ; б) y = x + 2 sinx ; в) y = 1+ cos2x .
С помощью программы можно построить графики и в полярной системе координат, а также линии, заданные параметрически. Кроме того, она чертит графики и направления, которые задаются с помощью уравнений или неравенств, выполнение которых на уроках занимают большое количество времени. Рассмотрим результатат построения такого графика.
№5. В полярных координатах построить графики следующих функций
(выполнить построение последовательно на одном графике):
1) R( a ) = 4 sin 4 a ; 2) x ( t ) = 8 cost – 2 cos 4 t и y ( t ) = 8 sint – 2 sin 4 t ;
3) ( x 2 + y 2 ) 2 – 54( x 2 — y 2 ) = 0 – в декартовой системе координат [2] (рис 6).
№6. Для самостоятельного выполнения. Построить график функции:
1) y = ׀ x 2 – 5 x + 6 ׀, ( y ( x ) = abs ( x ^2 – 5* x +6))
2) y = ׀ x 2 – 5 ׀ x ׀ + 6 ׀, ( y ( x ) = abs ( x ^2 – 5 abs ( x ) +6)
3) y = ׀׀ x 2 ׀ -5 ׀ x ׀ +6 ׀, ( y ( x ) = abs ( abs ( x ^2) – 5 abs ( x ) +6)
III. Подведение итогов урока.
IV. Домашнее задание: записать алгоритм построения графиков задания № 6.
- Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.(в двух частях). Ч.1: учебник для общеобразовательных учреждений. – М.: Мнемозина, 2005.
- Азевич А.И . Advanced Grapher на уроке и после него // Математика в школе. – 2001. — №6. – С. 69.
📺 Видео
Advanced Grapher xeol.com.uaСкачать

Advanced Grapher, derivative xeol.com.uaСкачать

Асимптоты функции. Горизонтальная асимптота. 10 класс.Скачать

Advanced Grapher xeol.com.uaСкачать

Graph построение графиковСкачать

Выпуск №2 Программа для построения графиковСкачать

Площадь плоской фигуры в Advanced GrapherСкачать

Исследование точек разрыва функций. Графическое построение наклонных асимптот в MS ExcelСкачать

Строим графики математических функций с помощью Advanced GrapherСкачать

Построение графика экспоненциальной функции | Функции и Графики | Алгебра IIСкачать

Селезнёва Ирина Алексеевна. Организация обучения класса решению задач с параметрамиСкачать

Grapher 19 Добавление осей и скругление кривых линий - Видеоурок №3Скачать

Graphing Horizontal and Vertical Asymptotes in PracticeСкачать

Grapher 11 Знакомство с интерфейсом - Видеоурок №1Скачать

Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Исследование функции. Построение графика. Высшая математикаСкачать