Уравнение акустического тракта эхо метода (6 видео)

Содержание

Акустический тракт.
РАСЧЕТ ЭХОСИГНАЛОВ
Методическое пособие на тему “Физические основы ультразвукового метода НК” Специальность: дефектоскописты вагонных, локомотивных депо (стр. 4 )
📺 Видео

Видео:Мастер класс по ультразвуковой диагностике в эхокардиографииСкачать

Акустический тракт.

Акустическим трактом называют путь ультразвука от излучателя до дефекта и затем к приемнику. Формулы акустического тракта определяют ослабление ультразвукового сигнала на этом пути.

В самом упрощенном виде можно сказать, что при контроле эхо-методом с увеличением расстояния до дефекта и уменьшением его размеров амплитуда эхо-сигнала от него уменьшается. Это уменьшение с увеличением расстояния происходит особенно быстро для небольших отражателей и медленнее для протяженных, например, донного сигнала. Однако из этих общих правил имеется ряд исключений, о которых будет сказано позднее.

Амплитуда сквозного сигнала при контроле теневым методом, также как донный сигнал, медленно уменьшается с увеличением расстояния между излучателем и приемником. Чем больше затеняющий дефект, тем сильнее ослабление амплитуды.

Отражатель плоской формы, например, диск, который при экспериментах заменяют искусственным дефектом в виде отверстия с плоским дном (рис. 2.27) такого же диаметра, как диск, даст эхо-сигнал больший, чем сфера того же диаметра, если он ориентирован так, что УЗ лучи отражаются зеркально, т.е. при контроле совмещенным преобразователем лучи падают на отражатель перпендикулярно (а). В этом, случае амплитуда растет пропорционально увеличению площади диска, конечно, до определенного предела. Но если такой отражатель наклонен (б), то зеркально отраженные лучи не попадают на совмещенный преобразователь. В результате амплитуда эхо-сигнала резко уменьшается. Это особенно заметно для большего диска, а для маленького влияние ориентации на амплитуду не так велико.

На амплитуду отражения влияет также то, чем заполнен дефект. Хорошо отражает ультразвук дефект, заполненный воздухом или другим газом, и гораздо хуже дефект, заполненный окислом, плотным шлаком или другим твердым веществом. Плохо отражают ультразвук очень тонкие (раскрытием в сотую долю микрометра) воздушные промежутки, которые получают при очень сильном сжатии металла. Тонкие окисные плены практически не дают заметного отражения сигнала.

Формулы для расчета амплитуд эхо-сигнала от некоторых отражателей (рис. 2.28), расположенных в дальней зоне для прямого совмещенного преобразователя, имеют вид:

для отражения от диска или плоскодонного отверстия — ;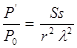

для отражения от сферы или отверстия со сферическим дном — ;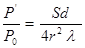

для отражения от боковой поверхности цилиндрического отверстия — ;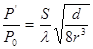

для донного сигнала (плоскости) — ;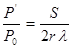

где Р₀ и Р’ – амплитуды излученного и принятого преобразователем сигналов; S – площадь пьезоэлемента преобразователя; — расстояние от преобразователя до отражателя; l — длина волны; s – площадь диска или дна плоскодонного отверстия; d – диаметр цилиндра или сферы.

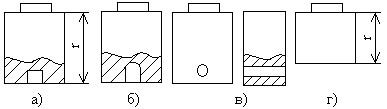Уравнение акустического тракта эхо метода

Рис. 2.28. Отражатели: а) плоскостное отверстие; б) отверстие со сферическим дном; в) боковое цилиндрическое отверстие, r – плоскость (донный сигнал).

Это формулы для максимальных эхо-сигналов, которые достигаются, когда отражатель находится на оси преобразователя и ориентирован перпендикулярно направлению УЗ лучей.

Поясним физический смысл этих формул. Площадь преобразователя входит в числитель всех формул, потому что лучи от него расходятся в виде диаграммы направленности. Угол расхождения лучей тем меньше, чем больше площадь преобразователя.

Дискообразный отражатель подобен излучающему преобразователю. От него лучи также расходятся в виде диаграммы направленности, поэтому площадь диска входит в числитель первой формулы.

Сравнение формул показывает, что ослабление донного сигнала с расстоянием происходит медленнее (пропорционально 1/r), чем эхо-сигнала от диска или сферы (пропорционально 1/r 2 ). Ослабление эхо-сигнала от цилиндра – в промежутке между ними, по закону (1/r) 3/2 . Такие закономерности объясняются следующим. Лучи от излучателя расходятся, поэтому амплитуда убывает как 1/r. Диск или сфера – как бы вторичные излучатели. Попавший в них сигнал переизлучается в обратном направлении (рис. 2.29, а) поэтому амплитуда опять убывает как 1/r. В итоге ослабление пропорционально 1/r 2 .

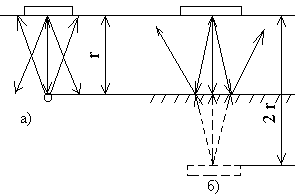
Донная поверхность играет роль зеркала (рис. 2.29,б). Отраженные от него лучи можно рассматривать, как излученные мнимым излучателем, показанным штриховыми линиями. Расстояние от него до приемника – 2r. Именно по закону 1/2r убывает донный сигнал.

Цилиндр в плоскости, перпендикулярной оси, — маленький отражатель, лучи от которого расходятся как от сферы. В плоскости вдоль оси – отражение происходит, как от зеркала. Отсюда закономерность (1/r) 3/2 .

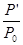
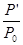
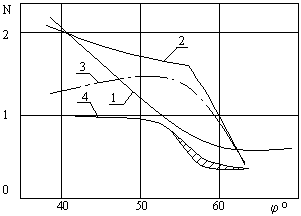
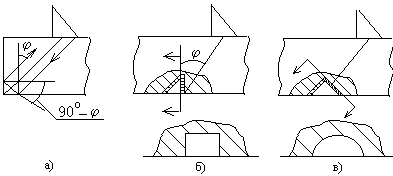
Ослабление сигнала , определяемое приведенными формулами называют дифракционным ослаблением. Дополнительное ослабление отношения вносит затухание ультразвука. Чтобы учесть его все формулы нужно умножить на ехр(-2dr), где d – коэффициент затухания.

Приведенные формулы справедливы, только когда диаметры диска, сферы или цилиндра больше длины волны. Если они меньше длины волны, то амплитуда отражения с уменьшением диаметра убывает, как правило, быстрее в результате огибания дефекта волнами. С учетом этого говорят, что дефекты меньше длины волны плохо выявляются. Для отражения от плоскодонного отверстия или отверстия со сферическим дном формулы остаются справедливыми, даже если их диаметры меньше длины волны, т.к. боковые стенки препятствуют огибанию.

При контроле наклонным преобразователем важное значение имеют угловой эффект. Он заключается в получении большой амплитуды эхо-сигнала от дефекта вблизи поверхности изделия благодаря двукратному отражению ультразвука от этой поверхности и дефекта. На рис. 2.30 показаны два таких отражателя: двугранный угол (а) и зарубка (б). При использовании поперечных волн амплитуда сигнала от первого из них равна амплитуде донного сигнала умноженной на коэффициент G’, а от второго – амплитуде эхо-сигнала от диска, площадь которого равна площади отражающей грани зарубки s’, умноженной на коэффициент G. Кривые изменения этих коэффициентов (рис. 2.31) от угла падения на поверхность j и глубины зарубки h учитывают эффекты трансформации волн и незеркального отражения.

Трансформация поперечной волны в продольную, на вертикальной поверхности отражателя возникает, когда угол падения на нее 90° — j больше, чем третий критический угол j’ (для стали j’ =33°) и вызывает резкое уменьшение G и G’ при углах j » 55 …65°. Незеркальное отражение увеличивает эхо-сигнал при углах j несколько больших третьего критического значения.

Сегментный отражатель (рис. 2.30,в) имеет отражающую грань, перпендикулярную направлению акустической оси. Эхо-сигнал от него такой же, как от диска равной площади, экспериментально это подтверждено для поперечных волн и углов a » 38 — 55°.

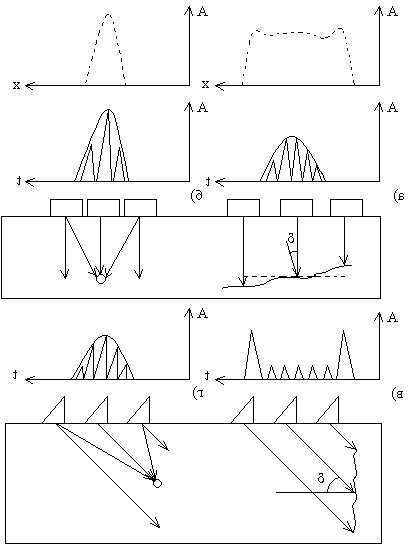
При перемещении преобразователя над дефектом (рис. 2.32) амплитуда эхо-сигнала изменяется. Расстояние от преобразователя до отражателя также будет изменяться. Соответственно перемещается эхо-сигнал на линии развертки. Линия, соединяющая вершины эхо-сигналов на экране дефектоскопа при перемещении преобразователя, называется огибающей. Изменение амплитуды эхо-сигнала в зависимости от перемещения преобразователя по поверхности изделия х будем называть огибающей по перемещению. На рис. 2.32, а) и б) огибающей по времени t показаны сплошными линиями, а по перемещению х – пунктирными.

Если дефект – небольшой диск, сфера или цилиндр (его поперечное сечение), то изменение амплитуды соответствует ее изменению в поперечном сечении поля излучения – приема I2 (рис. 2.32, б и г). Для протяженного и непротяженного (компактного) дефектов форма и ширина обеих огибающих существенно отличаются. Это позволяет сделать вывод: протяженный или непротяженный дефект обнаружен, оценить его размеры, наклон к поверхности. С этой целью измеряют ширину обеих огибающих на определенном уровне: 6, 10 или 20 дБ ниже максимального значения амплитуды эхо-

сигнала от этого дефекта, а иногда – на уровне фиксации, ниже которого эхо-сигналы вообще не регистрируют.

Например, если дефект – расслоение параллельное поверхности, показанное на рис. 2.32,а) штриховой линией, то огибающая по времени будет очень узкой, как на рис. 2.32,б), а по перемещению – широкой. Если дефект наклонен к поверхности – огибающая по времени расширяется (как А(t) на рис.2.32,а).

Сравнение огибающих выполняют, используя в качестве исходной огибающую от бокового цилиндрического отражателя (рис. 2.32, б и г), как это было сделано в примере, приведенном выше. Такой дефект отражает одинаково при любом направлении падающей волны – имеет равномерную индикатрису рассеяния. Если дефект плоский (например, дискообразный) то индикатриса рассеяния будет неравномерной. Максимум будет наблюдаться в направлении близком к зеркальному отражению.

Аналогично используют наблюдения за изменением амплитуды сквозного и донного сигналов при контроле теневым или зеркально-теневым методами. В этом случае существует только огибающая по перемещению.

Видео:Звук, характеристики звука, акустический резонанс, эхо. 9 класс.Скачать

РАСЧЕТ ЭХОСИГНАЛОВ

2.2.1. Понятие акустического тракта

Акустическим трактом называют путь ультразвука от излучателя до дефекта или другого препятствия и затем к приемнику колебаний. Формулы акустического тракта определяют ослабление сигнала на этом пути, т. е. амплитуду сигнала от отражателя. Для упрощения математических выкладок ниже рассмотрим акустический тракт для жидкой среды и затем введем поправки, характерные для твердого тела. Обозначим через Р0 амплитуду сигнала, излучаемого преобразователем (акустического зондирующего импульса), а амплитуду принятого сигнала — через Р’. Задача » а

состоит в определении отношения Р'(Ро.

Естественные дефекты могут иметь самую различную форму, ориентацию и акустические свойства, которые заранее неизвестны, поэтому при анализе эхоме — тода формулы акустического тракта выводят для моделей дефектов в виде полых отражателей простой формы: тонкого диска, сферы, цилиндра, тонкой полосы, плоскости и т. д. Физическая реализация некоторых моделей дефектов представляет большие технологические трудности (например, трудно выполнить тонкий диск, не нарушая целостности окружающего твердого материала), поэтому при экспериментах и производственном контроле модели дефектов заменяют искусственными отражателями (рис. 2.10): диск — плоскодонным отверстием, сферу-—отверстием со сферическим дном и т. д. Амплитуды эхосигналов от моделей дефектов и искусственных отражателей мало отличаются, когда их размеры больше длины волны ультразвука. В противном случае амплитуды эхосигналов могут ие совпадать.

Наиболее широкое применение нашел искусственный дефект типа плоскодонного отверстия, который удовлетворительно имити-

рует небольшие расслоения, трещины. Он рекомендован рядом ГОСТов для настройки чувствительности дефектоскопа. Боковое цилиндрическое отверстие имитирует протяженные шлаковые включения, цепочки пор. Его просто изготовить в производственных условиях. Оно равномерно отражает волны независимо от их направления (в плоскости, перпендикулярной оси). Его используют во многих отечественных и иностранных стандартных образцах.

Протяженная плоскость соответствует донному сигналу, по которому удобно выполнять настройку. Кроме того, она имитирует протяженные расслоения. Цилиндрическую вогнутую поверхность используют в стандартных образцах для получения максимального эхосигнала и определения точки ввода преобразователя (см. ниже).

Вопросы дифракции плоской акустической волны на некоторых отражателях рассмотрены в § 1.4. Здесь будет показано, как использовать результаты дифракционной теории для расчета акустического тракта, т. е. как учесть особенности полей излучения и приема преобразователя. Кроме того, в этом разделе изложены приближенные и (более простые) способы расчета отражения, пригодные, когда размеры отражателя больше длины волны: энергетическое приближение, основанное на представлениях лучевой акустики, и метод Кирхгофа. Согласно последнему каждую точку «освещенной» поверхности плоского отражателя рассматривают как вторичный излучатель волн, а поле отраженной волны вне отражателя считают равным нулю. В приводимом далее выводе формул акустического тракта не учтено затухание ультразвука. Чтобы учесть этот эффект, следует ввести во все формулы для контактных прямых преобразователей множитель е_2вг, где г — расстояние от преобразователя до отражателя, а для преобразователей с акустической задержкой — множитель є

Видео:ЭХО-КГ. Основы УЗИ сердца. Подготовка и основные доступы: парастернальный, субкостальный, апикальныйСкачать

Методическое пособие на тему “Физические основы ультразвукового метода НК” Специальность: дефектоскописты вагонных, локомотивных депо (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4

Падение волны на границу двух твёрдых сред при наличии жидкостной прослойки.

14. Энергетические соотношения (при нормальном падении волн).

Если на пути распространения ультразвуковой волны встречается другая среда (среда с другими акустическими свойствами), то одна часть энергии проходит во вторую среду, а другая часть — отражается в первую. Распределение энергии между отраженной и прошедшей волнами определяется соотношением их акустических свойств (удельных акустических сопротивлений сред).

Коэффициентом прозрачности границы называют – соотношение интенсивности или амплитуды волны прошедшей через границу раздела сред, к волне падающей на границу, соответственно коэффициентом отражения – отражённой волны к падающей.

= от 0 до 1;

=от 0 до l ;

На отражении упругих волн от несплошностей основана выявляемость дефектов при эхо-дефектоскопии, так как по своим акустическим свойствам несплошности (трещины, поры, шлаковые включения и др.) отличаются от основного материала.

Коэффициент отражения от трещин и пор близок к единице, если величина раскрытия больше 0,0001 мм.

Зеркальное отражение – возникает в том случае, когда высота неровностей поверхностей во много раз меньше длины волны.

Дефекты с зеркальными поверхностями эхо импульсным методом выявляются плохо. Угол отражения от таких поверхностей равен углу падения.

Диффузное отражение – возникает, если высота неровностей поверхностей соизмерима с длиной волны.

При наклонном падении коэффициенты отражения и прозрачности зависят как от соотношения акустических сопротивлений граничащих сред, так и от угла падения. На графике показана зависимость коэффициентов прозрачности по энергии при падении продольной волны из оргстекла на сталь (толщина контактного слоя масла близка к нулю).

При увеличении прослойки, становиться меньше коэффициент прозрачности.

Газообразный слой в твёрдом теле, даже при минимальной толщине обладает очень хорошей отражающей способностью. Например для при толщине газообразного слоя порядка , где — длина волны в слое (при ). Для при нормальном падении, коэффициент отражения R=1, независимо от толщины слоя.

Коэффициент отражения границы стали с другим материалом

Коэффициент отражения по интенсивности, R,%

Из таблицы видно, что шлаковые включения будут выявляться гораздо хуже дефектов таких же размеров, но с воздушным заполнением. Приведенные значения справедливы для несплошностей, размеры которых намного больше длины волны. Если же размеры несплошности в направлении, перпендикулярном УЗ лучу, значительно меньше длины волны, то волны огибают ее без существенного отражения. Для получения заметного отражения достаточно, чтобы размеры несплошности были соизмеримы с длиной волны.

ПРИМЕЧАНИЕ: Правила и законы, описанные выше справедливы только в определённых рамках или при определённых условиях говорят, что это верно если, действуют законы геометрической акустики (лучевой теории распространения волн).

Основные условия применимости законов геометрической акустики

1. Размеры отражателя более 2-3х длин волн (2в> (2-3), в противном случае геометрическая акустика не действует, так как велик вклад рефракционных поправок.

2. Расстояние то излучателя до отражателя и от отражателя до приёмника много больше длины волны , так как фронт волны можно считать плоским, только при значительных расстояниях.

3. Отражающие поверхности, имеющие незначительные неровности, т. е. являются зеркальными 2h* cosb l/4. Остальные поверхности диффузные.

14. Импульсный режим излучения ультразвуковых колебаний

В современных дефектоскопах в основном используют импульсный режим излучения ультразвуковых колебаний. При этом периодически излучают кратковременные импульсы с высокочастотным (ВЧ) заполнением. Импульсы ультразвуковых колебаний, излучаемые в контролируемое изделие, называются зондирующими.

Основные параметры упругих волн.

— длительность зондирующего импульса

— Высокочастотное заполнение импульса

— амплитуда размаха

Длительность зондирующих импульсов

Длительность зондирующих, импульсов измеряют обычно на уровне 0,1 от максимального значения U. В зондирующем импульсе, как правило, содержится от 4 до 12 периодов колебаний с ультразвуковой частотой f. Период этих колебаний, То для традиционной в дефектоскопии частоты ультразвуковых колебаний fо = 2,5 МГц равен:

То =1/fо = 1/2 Гц = 0,0000004 с = 0,4 мкс.

В практике используется длительность зондирующих импульсов tи = 1,6-5,0 мкс.

Чем длиннее зондирующий импульс, тем мощнее излучаемые колебания и тем глубже можно озвучить контролируемое изделие. В то же время, чем короче зондирующий импульс, тем лучше разрешающая способность дефектоскопа по дальности и меньше «мертвая» зона. Поэтому выбор длительности зондирующего импульса — решение компромиссное.

4 периода колебаний с частотой f0 9 периодов колебаний с частотой f0

Частоту заполнения fо зондирующих колебаний, как уже отмечалось выше, выбирают, исходя из минимальных размеров требующих выявления дефектов, с одной стороны, и максимальных размеров зерен материала, из которого изготовлено контролируемое изделие — с другой.

Размеры зерен, в свою очередь, влияют на коэффициент затухания ультразвуковых волн в материале изделия. Необходимо, чтобы длина ультразвуковой волны λ была сравнима с минимальным размером обнаруживаемого дефекта и намного больше размера зерна металла.

Не путайте частоту f0 ультразвуковых колебаний, которая составляет миллионы колебаний в секунду (1—10,0 МГц), и частоту посылок зондирующих импульсов F, составляющую всего лишь сотни и тысячи импульсов в секунду (100—4000 Гц).

Частота следования зондирующих импульсов

Частота следования зондирующих импульсов, используемая в различных дефектоскопических средствах, зависит от скорости перемещения ультразвукового преобразователя по контролируемому изделию. Таким образом, чем быстрее перемещаются ультразвуковые преобразователи по контролируемому изделию, тем чаще должны посылаться ультразвуковые колебания.

Амплитуда зондирующих импульсов U — это максимальная величина электрического импульса, прикладываемого к пьезопластине ПЭП. Амплитуда U может достигать до 500 В на 1 мм толщины пластины из пьезо-керамики. В дефектоскопах для контроля рельсов амплитуда зондирующего импульса составляет 50—200 В. Как правило, если зондирующий импульс имеет экспоненциально затухающую форму, требуется прикладывать к пьезопластине большее напряжение, чем при возбуждении ее зондирующим импульсом колоколо-образной формы.

В связи с тем, что зондирующий импульс не всегда имеет симметричную форму относительно горизонтальной (временной) оси, для характеристики амплитудного параметра импульса используют величину размаха Uр первого периода колебаний. В радиотехнике импульс напряжения с высокочастотным заполнением называют радиоимпульсом. Таким образом, электрические колебания, подаваемые для возбуждения пьезопластины, то есть зондирующий импульс, представляют собой радиоимпульс. При выделении амплитудной огибающей этого импульса образуется видеоимпульс. Дефектоскопист на экране дефектоскопа наблюдает в виде видеоимпульсов эхо-сигналы, которые формируются при выделении огибающих радиоимпульсов с помощью амплитудного детектора.

15. Акустическое поле наклонного преобразователя

Поле излучения-приема наклонного преобразователя

Особенность акустического поля наклонного ПЭП состоит в том, что УЗ волны излучаются в материал призмы, а затем, испытав преломление на границе, попадают в изделие. Это сильно изменяет ближнее поле преобразователя. Распределение энергии в ближнем поле становится равномерным, отсутствуют четко выраженные максимумы и минимумы.

Поле в дальней зоне образуют лучи диаграммы направленности, которые возникли уже в призме ПЭП, а затем преломились на границе призмы с изделием. При этом ослабление каждого луча определяется коэффициентом прозрачности для данного угла падения.

В результате в плоскости падения акустической оси диаграмма направленности расширяется вследствие преломления, так как угол преломления возрастает тем быстрее, чем больше угол падения. Диаграмма направленности становится несимметричной. Амплитуда поля оказывается более высокой в нижней части, где расхождение лучей меньше, а интенсивность — больше. Это явление выражено тем сильнее, чем больше угол призмы ПЭП,

При расчете расстояния от преобразователя до дефекта в плоскости падения волны допустимо преобразователь заменить мнимым излучателем — приемником с центром в точке О1, Точка О1, располагается на продолжении преломленной акустической оси на расстоянии

граница раздела сред

; где

г, — действительный путь ультразвука в призме;

п — скорость продольной волны в призме ПЭП;

Сt — скорость поперечной волны в изделии.

В сечении плоскостью, проходящей через преломленную акустическую ось и перпендикулярной плоскости падения, поле остается симметричным. Диаграмма направленности будет такой же, как если бы поперечные волны непосредственно излучались в изделие мнимым источником с центром в точке, расположенной на расстоянии г» от точки О’:

r» = С/С,

Плоскость падения волны – называется основной плоскостью, также имеет место быть дополнительная плоскость падения волны.

Размер мнимого излучателя и его место положения не сложно находится в тригонометрических отношениях, в частности в плоскости падения имеет место связь:

, где

— размер мнимого излучателя

Ясно, что , а значит дальняя зона ДН в плоскости падения волны при наклонном вводе – шире, чем при нормальном, причём, чем больше b, тем больше a.

В дополнительной плоскости угол b не меняется, а значит в дополнительной плоскости, размер мнимого излучателя равен: .

Форма мнимого излучателя – эллипс. Таким образом Диаграмма направленности (ДН) наклонного ПЭП – различна в основной и дополнительной плоскости.

16. Расчет акустического тракта прямого контактного преобразователя

Акустическим трактом УЗ дефектоскопа называют путь УЗ импульса от излучателя до отражателя и затем — обратно к приемнику ультразвука. При расчете акустического тракта ставится задача определить амплитуду сигнала от дефекта в зависимости от акустических свойств материала, частоты ультразвука, размеров и формы пьезоэлектрического преобразователя (ПЭП) и дефекта и расстояния между ними.

Естественные дефекты могут иметь самую различную форму, ориентацию и акустические свойства, которые заранее не известны. Поэтому уравнение акустического тракта решается обычно для искусственных дефектов, то есть полых отражателей достаточно простой геометрической формы.

Для анализа уравнений акустического тракта важное, значение имеют понятия полей излучения и приема ПЭП УЗ дефектоскопа. Поле излучения ПЭП определяется амплитудой сигнала, действующего на элементарный приемник, помещаемый в различные точки пространства. Поле приема определяется амплитудой сигнала приемного ПЭП при действии на него малого сферического излучателя, помещаемого в различные точки пространства.

В практике дефектоскопии часто ПЭП служит одновременно излучателем и приемником ультразвука. Для определения его приемно-излучающих характеристик целесообразно проанализировать акустический тракт при отражении ультразвука от сферы, диаметр которой значительно меньше длины волны. Такую сферу можно рассматривать как вторичный сферический излучатель, амплитуда сигнала которого пропорциональна амплитуде падающей волны. В результате амплитуда отражения от такого дефекта пропорциональна С(г)*С(г’), то есть произведению полей излучения и приема.