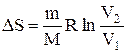Уравнение адиабаты в p t (3 видео) | Про уравнения

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Содержание

Кратко об идеальном газе
Что это адиабатический процесс?
Уравнения Пуассона для адиабатического процесса
Пример задачи
Адиабатический процесс
Что такое адиабатический процесс
Что такое адиабата
Адиабатический процесс. Политропный процесс.
🔍 Видео

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Адиабатный процесс. 10 класс.Скачать

Что это адиабатический процесс?

Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

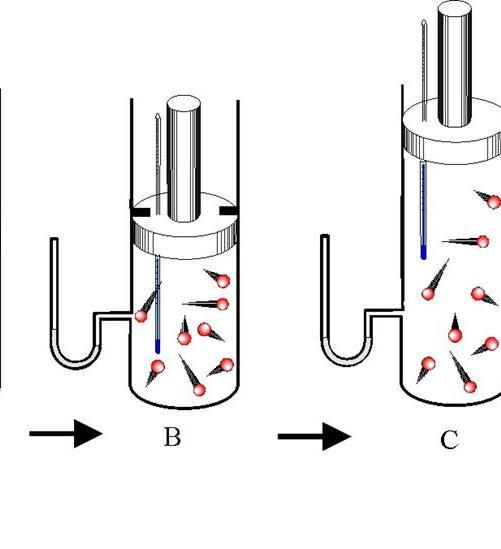
Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

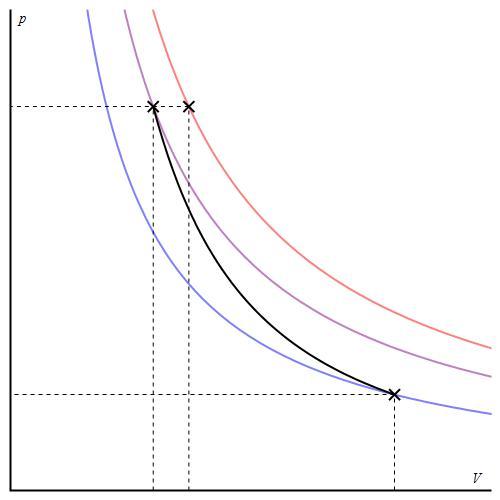
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:Адиабатическое охлаждение.Скачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

Видео:Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Адиабатический процесс

Вы будете перенаправлены на Автор24

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Что такое адиабатический процесс

Адиабатическим или адиабатным процессом называют процесс, при котором отсутствует теплообмен с окружающей средой ($delta Q=0$).

В таком случае первое начало термодинамики можно записать в виде:

[0=fracnu RdT+pdV left(1right).]

Из уравнения (1) следует, что при увеличении объема в адиабатном процессе уменьшается температура системы. Или говорят, что в адиабатном процессе работа совершается за счет уменьшения внутренней энергии системы. И обратное справедливо: работа, совершенная над системой, увеличивает внутреннюю энергию системы и, как следствие, температуру. Уравнение, которое характеризует адиабатный процесс в термодинамических параметрах (уравнение адиабаты) носит имя Пуассона. Получим это уравнение для идеального газа. Из уравнения состояния идеального газа:

Из соотношения Майера:

[C_p-C_V=nu R left(3right).]

Подставим (3) в (2), получим:

Разделим уравнение (1) $C_VT ( C_V=fracнR)$, получим:

где $gamma =frac$ — показатель адиабаты. Проинтегрируем уравнение (5):

где $lnA$- некоторая постоянная.

Потенцируем уравнение (6), получаем:

Уравнение (7) есть уравнение адиабаты в параметрах T,V. Для того, чтобы перейти к уравнению адиабаты, в параметрах p,V используют уравнение Менделеева — Клайперона. И получают уравнение адиабаты в виде:

Или в параметрах p,T уравнение (7,8) имеет вид:

Зная, что теплоемкости можно представить как:

показатель адиабаты исходя из ($gamma =frac$) и уравнений (10)

Легко получить формулу работы для адиабатного процесса. По определению работа газа A равна:

где $p_1V_1=nu RT_1.$ Используя уравнение адиабаты, записанное для двух состояний в параметрах $V,T$, получаем:

Видео:Адиабатное расширениеСкачать

Что такое адиабата

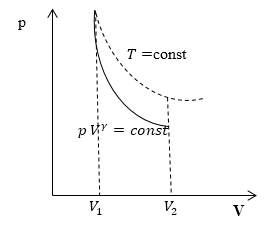
Линия, изображающая на термодинамической диаграмме адиабатный процесс, называется адиабатой (рис.1).

Для сравнения на рис. 1 представлена также изотерма (пунктиром). На рис. 1 видно, что адиабата идет круче, чем изотерма. Работа в адиабатическом процессе по расширению от объема $V_1 $до $V_2$ меньше, чем в изотермическом процессе с таким же изменением объема. Это объясняется тем, что при адиабатном процессе происходит охлаждение газа. В изотермическом процессе при расширении давление уменьшается только за счет уменьшения плотности, тогда как в адиабатном за счет плотности и средней кинетической энергии молекул (соответственно температуры).

Задание: Одноатомный газ совершает адиабатное расширение от объема $V_1=$1$м^3 $при температуре $Т_1=400 К$, при этом давление газа изменяется от $p_1=5cdot ^6Па $до $p_2=2cdot ^6 Па$. Найдите объем газа в конечном состоянии.

При адиабатном расширении имеем:

где $gamma =frac , $так как газ одноатомный, то i=3, следовательно, $gamma =frac=frac$. Значит можно выразить интересующий нас объем:

Ответ: Объем газа в конечном состоянии 4,6 $м^3.$

Задание: Некоторую массу газа сжали так, что $frac=5$, в первом случае процесс проводился адиабатический, второй изотермический. Начальные состояния газов одинаковы в том и другом случае. Найти отношение работ $frac =?$

Работа в адиабатном процессе задана формулой над газом:

Формула для работы в изотермическом процессе имеет вид:

Тогда найдем искомое отношение:

Для коэффициента адиабаты мы знаем формулу вычисления через число степеней свободы$(i)$, а для одноатомного газа $i=3$:

Подставим данные из условий задачи, получим:

Ответ: Отношение работ, которые совершают над газом в процессах сжатия в адиабатном процессе и изотермическом равно 1,89. Работа над газом в адиабатном процессе больше.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 11 2021

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Адиабатический процесс. Политропный процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, адиабатическим процессом можно считать процесс в двигателях внутреннего сгорания(расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д.

Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что

dА=-dU, (2.6.1)
т.е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражение для произвольной массы газа перепишем уравнение в виде

. (2.6.2)

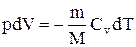
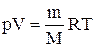
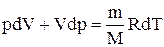
Продифференцировав уравнение состояния для идеального газа , получим

. (2.6.3)
Исключим из (2.6.2) и (2.6.3) температуру Т:

.
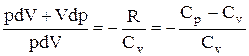
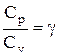
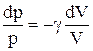
Разделив переменные и учитывая, что найдем

Интегрируя это уравнение в пределах от p₁ до р₂ и соответственно от V₁ до V₂, а затем потенцируя, придем к выражению

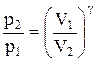
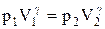
Так как состояния 1 и 2 выбраны произвольно, то можно записать

PV g =const. (2.6.4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из (2.6.4) с помощью уравнения Клапейрона-Менделеева:

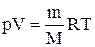
соответственно давление или объем:

(2.6.5)

. (2.6.6)

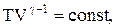
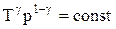
Эти выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

(2.6.7)
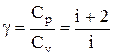
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, g =1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, g =1,4. Значения вычисленные по формуле (2.6.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабат а) в координатах р, V изображается гиперболой (рис. 2.6.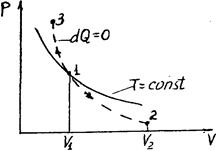1).

Рис. 2.6.1

На рисунке видно, что адиабата ( 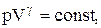) более крута, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Вычислим работу, совершаемую газом в адиабатическом процессе.
Запишем уравнение в виде

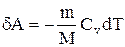
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до Т₂ и работа расширения идеального газа

. (2.6.8)

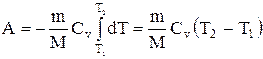
Применяя те же приемы, выражение (2.6.8) для работы при адиабатическом расширении можно преобразовать к виду

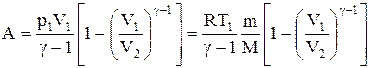
Работа, совершаемая газом при адиабатическом расширении 1-2 (определяется заштрихованной площадью, выполненной на рис. 61), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_v и С_p, в изотермическом процессе (dT=0) теплоемкость равна ±¥, в адиабатическом (dQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const), можно вывести уравнение политропы:

pV n =const, (2.6.9)
где 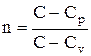— показатель политропы. Очевидно, что при С=0, n=gполучается уравнение адиабаты; при С=¥, n=l — уравнение изотермы; при С=С_p, n=0 — уравнение изобары, при С=С_v , n=±¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

2.7 Круговой процесс (цикл).
Обратимые и необратимые процессы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 2.7.1).

Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1-2) и сжатия (2-1) газа. Работа расширения (определяется площадью фигуры 1а2V₂V₁) положительна (dV > 0), работа сжатия (определяется площадью фигуры 2blV₁V₂2) отрицательна (dV 0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 2.7.1,а), если за цикл совершается отрицательная работа 0. (2.8.4)

Выражения (2.8.3) и (2.8.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (2.8.3) и (2.8.4) можно представить в виде неравенства Клаузиуса

DS 0, (2.8.5)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2.8.2), изменение энтропии

, (2.8.6)
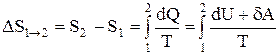
где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (2.8.6) определяет энтропию лишь с точностью до аддитивной постоянной.

Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (2.8.6), найдем изменение энтропии в процессах идеального газа. Так как

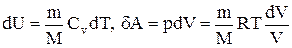
то ,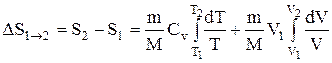

или 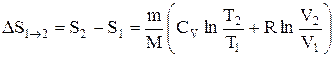, (2.8.7)

т.е. изменение энтропии 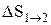идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1®2.

Так как для адиабатического процесса dQ=0, то DS=0 и, следовательно, S=const, т.е. адиабатический обратимый процесс протекает при постоянной энтропии. Из формулы (2.8.7) следует, что при изотермическом процессе (T₁=T₂)

при изохорном процессе (V₁ =V₂)

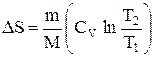
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему.

Более глубокий смысл энтропии вскрывается в статистической физике, энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S=kInW, (2.8.8)
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
Так как реальные процессы необратимы, то можно утверждать, что все
процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных к более вероятным.

Сопоставляя выражения (2.8.5) и (2.8.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.