Уравнение адиабаты и ее графическое изображение в координатах p v p t v t (5 видео)

Содержание

Адиабатный процесс. Вывод уравнения адиабаты
Адиабатный процесс. Изопроцессы в термодинамике
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи
Кратко об идеальном газе
Что это адиабатический процесс?
Уравнения Пуассона для адиабатического процесса
Пример задачи
🔍 Видео

Видео:Адиабатный процесс. 10 класс.Скачать

Адиабатный процесс. Вывод уравнения адиабаты

При адиабатном процессе отсутствует теплообмен между системой и окружающей средой — dQ = 0. К таким процессам можно отнести быстропротекающие процессы, а также процессы с хорошей теплоизоляцией. Например, адиабатным процессом можно считать распространение звука в среде, поскольку скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатные процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.

Из первого начала термодинамики при dQ = О имеем dU + dA=О,

или

Таким образом, внешняя работа при адиабатном процессе совершается за счет изменения внутренней энергии системы. При этом если газ расширяется, совершая работу против внешних сил, то его внутренняя энергия и температура уменьшаются. А при адиабатном сжатии температура газа повышается. Это явление используется, например, в дизельных двигателях для воспламенения горючей смеси.

Уравнение (12.23) с помощью выражений для работы и приращения внутренней энергии может быть переписано в виде

Добавив к этому уравнению дифференциал от уравнения Менделеева- Клапейрона

получим систему двух уравнений. Поделив почленно уравнение (12.25) на уравнение (12.24), имеем: . Воспользовавшись уравнением Майера, получим после преобразований

Последнее уравнение допускает разделение переменных:

где введено обозначение показателя адиабаты

Интегрируя полученное дифференциальное уравнение соответственно в пределах ot/?i до р2 и от V до Уг с последующим потенцированием, получим

или

Поскольку состояния 7 и 2 выбраны произвольно, то можно переписать (12.27) в виде

Полученное выражение называют уравнением адиабаты, или уравнением Пуассона. Заметим, что показатель адиабаты всегда больше единицы. При нормальной температуре для одноатомных газов i = 3, у = 1,67; для двухатомных газов и других газов с линейной молекулой i = 5, у= 1,4; для газов с нелинейной молекулой / = 6, у — 1,33.

Воспользовавшись уравнением Менделеева-Клапейрона, несложно получить уравнение адиабаты в переменных Т, V:

или р, Г.-

График адиабатного процесса р = const/V Y в координатах р, V изображается более крутой кривой, чем изотерма (p=const/V, см. рис. 12.2). Это объясняется тем, что при адиабатном сжатии увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры в адиабатном процессе. Математически это выражается в формуле адиабатного процесса тем, что у>1.

Из (12.24) найдем работу при адиабатном процессе:

, откуда при интегрировании

Работа в координатах р, V находится путем исключения температуры из (12.31) либо по определению работы (12.3) с учетом (12.28)

Работа газа при адиабатном расширении меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатном расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне теплоты.

Следует отметить, что поскольку для адиабатного процесса теплообмен с окружающей средой отсутствует и dQ = 0, то теплоемкость (в соответствии с определением) равна нулю.

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Адиабатный процесс. Изопроцессы в термодинамике

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы будем работать с уже известными нам физическими понятиями, но в несколько иной области применения. А именно с изопроцессами в термодинамике. Мы рассмотрим, какие изменения в первый закон термодинамики (закон сохранения энергии в тепловых процессах) внесут протекания этих самых процессов при неизменном макроскопическом параметре газа. Также мы рассмотрим новый, ранее неизвестный процесс – адиабатный.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Видео:Урок 163. Задачи на графики процессов в газахСкачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Физика Изучение графиков изопроцессовСкачать

Что это адиабатический процесс?

Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

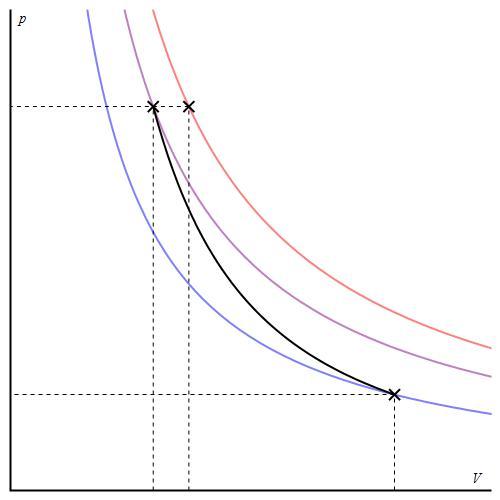
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.