Уравнение адиабаты для давления и температуры (6 видео)

Новое в блогах

Содержание

Физический смысл адиабатного процесса (Часть 1 — Давление газа)
Адиабатный процесс. Изопроцессы в термодинамике
Адиабатный процесс, его суть и и формулы
Связь с первым началом термодинамики
Следствие из первого начала термодинамики для адиабатического процесса
Адиабатный процесс. Формулы
Уравнение адиабаты
Первичное выражение
Вторичное выражение. Подстановка значения
Примеры адиабатных процессов
Заключение
📺 Видео

Видео:Адиабатный процесс. 10 класс.Скачать

Физический смысл адиабатного процесса (Часть 1 — Давление газа)

1. Это первая часть статьи, которую я планирую написать и опубликовать. Вторая часть будет посвящена температуре, третья — экспериментальной проверке теоретических выводов.

2. Приношу свои извинения за не совсем адекватное написание формул. Всем, кого заинтересовала эта статья, могу выслать на мыло вариант в формате docx с нормально написанными формулами (мой адрес — [email protected])

3. Приглашаю к сотрудничеству по разработке основных положений электромагнитной теории теплоты всех желающих

4. Продолжение следует.

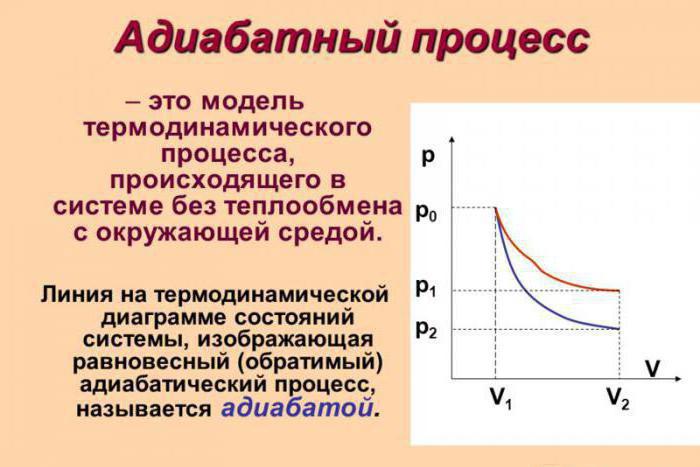
Хорошо известно, что при сжатии газа повышается его давление и его температура. Соответственно, при расширении газа температура и давление падают. Если при этом система (сжимаемый газ и ёмкость, в котором этот газ содержатся) не обменивается тепловой энергией друг с другом и с окружающим пространством, то такие процессы сжатия и расширения называются адиабатными (адиабатическими).

Современная теоретическая физика (статистическая физика, статистическая механика, физическая кинетика) до сих пор объясняет изменение давления и температуры газов работой, которая совершается над газами при их сжатии или которую совершает сам газ при расширении. См, например: ( http://ru.wikipedia.org/wiki/%C0%E4%E8%E0%E1%E0%F2%E8%F7%E5%F1%EA%E8%E9_%EF%F0%EE%F6%E5%F1%F1 )

Характер изменения величин давления и температуры газов при адиабатном процессе в современной теоретической физике считается потенциальной функцией, основанием которой является занимаемый газом определенной массой объём V , а показатель зависит от т.н. показателя адиабаты k :

k = C (p) /C (V) , где

C_p и C_V — теплоёмкости газа при постоянном давлении и постоянном объёме, соответственно.

Для идеальных газов, с которыми так любит иметь дело современная теоретическая физика, теплоёмкости которых считаются постоянными, характер изменения давления и температуры определяется простейшими уравнениями:

p= const /V^ k =co nst V^ (- k ) ,

T= const/ V^ (k-1) =const V^ (1-k) , где

p – давление газа,

V – объем, занимаемый газом,

T – температура газа (абсолютная),

k – показатель адиабаты.

Тому же самому учат и все современные школьные учебники и курсы лекций по общей физике.

Современная теоретическая физика считает, что величина показателя адиабаты k равна 5/3 для одноатомных газов, 7/5 – для двухатомных и 4/3 – для трёхатомных газов. Изменение величины показателя адиабаты принято обосновывать количеством неких «степеней свободы» у газообразных молекул. Хотя абсолютно никакой логики и никакого физического смысла в попытке связать эти самые «степени свободы» с величиной показателя адиабаты нет.

Что же происходит при адиабатных процессах с газами согласно разрабатываемой мной электромагнитной теории теплоты (ЭТТ).

Согласно ЭТТ агрегатное состояние вещества определяется текущим распределением электронов атомов, входящих в состав молекулы. Существует три основным электронных уровня – газообразующий, в котором может находиться не более двух электронов, гидрогенный («жидкостной») и кристаллообразующий, в группах которых может содержаться максимум по 8 электронов. Таковы на сегодняшний день представления ЭТТ о строении атомов и молекул, сделанные на основе свойств элементов периодической таблицы Менделеева.

Молекула реального газа гелия (He), более всех других подходящего на роль «идеального» газа, представлена на рис. 1. Она имеет одноатомное молекулярное ядро, в состав которого входит два протона и два нейтрона, и два электрона, которые при нормальных условиях располагаются на газообразующем уровне – вращаясь по замысловатым траекториям вокруг молекулярного ядра, они создают вокруг него сферическое электронное «облако».

Рис. 1. Газообразная молекула He (гелия)

согласно электромагнитной теории теплоты.

Электроны, вращаясь вокруг молекулярного ядра, создают т.н. «электронное облако», которое индуцирует электрическое и магнитное поля. Эти поля, взаимодействуя с электрическими и магнитными полями, индуцируемыми электронами соседних молекул, и заставляют газообразные молекулы отталкиваться друг от друга, как одноимённые электрические заряды и одинаковые полюса магнитов. Эти силы отталкивания молекул друг от друга и приводят ко всем хорошо известным свойствам газов занимать весь предоставленный объём, рассеиваться в вакууме (космическом пространстве), обладать упругостью, создавать, вследствие действия силы притяжения к Земле, атмосферное давление, передавать давление в разных направлениях, например, звуковые волны и т.д. и т.п.

Предположим, мы имеем некий цилиндр с поршнем, наполненный молекулами «идеального» газа гелия (см. рис. 2 слева). Приложив к штоку поршня некоторую силу F , т.е. попросту надавив на поршень, мы уменьшили объём газа в n раз – например, как это показано на рис. 2 справа – вдвое.

Рис. 2. Адиабатное сжатие газа

согласно электромагнитной теории теплоты.

Вследствие сжатия газообразные молекулы гелия уплотнились, расстояния между молекулярными ядрами уменьшились. Соответственно, главные эквипотенциальные поверхности полей молекул сократились в размерах, – что наглядно изображено на рис. 2.

Кстати, рис. 2 наглядно отображает характер уплотнения молекул. Хотя сперва кажется, будто бы я просто-напросто не нарисовал половину молекул внутри цилиндра с поршнем. Присмотритесь внимательно – в каждом ряду молекул на рисунке справа – 9 штук, а слева – уже 11. Я не ошибся. При уменьшении объёма вдвое расстояние между молекулами уменьшается всего на одну пятую часть – см. рис. 3.

Рис. 3. Изменение соотношений длины ребра и площади грани куба

при уменьшении его объёма вдвое.

То есть, при уменьшении объёма в n раз расстояние между центрами газовых молекул сокращается в куб.корень из < n> раз.

Определим, в какой пропорции увеличиваются силы отталкивания между отдельными молекулами (см. рис. 4).

Рис. 4. Увеличение сил отталкивания между отдельными газовыми молекулами при сжатии газа.

Согласно закона Кулона, величина силы взаимодействия двух точечных зарядов прямо пропорциональна произведению модулей этих зарядов q ₁ и q ₂ и обратно пропорциональна квадрату расстояния R между ними:

k в данном случае – коэффициент пропорциональности.

Эта формула универсальна для всех известных полей – и для магнитного и для гравитационного. Для гравитационного поля, например, этой формулой описывается закон всемирного тяготения:

где γ — гравитационная постоянная, по сути – тот же самый коэффициент пропорциональности, а m ₁ и m ₂ – масса тел («гравитационный заряд»).

В нашем случае мы под обозначением q ₁ и q ₂ будем понимать условную сумму всех типов «зарядов», индуцирующих соответствующие поля – и электрического, и магнитного, и пытающегося им противостоять гравитационного (как известно, гравитационное поле создаёт лишь силы притяжения). Таким образом (см. рис. 4), до сжатия газа, отдельно взятые молекулы отталкивались друг от друга с силой:

а после сжатия – с силой:

Таким образом, при уменьшении объёма в n раз (специалисты в области двигателей внутреннего сгорания называют эту величину степенью сжатия) сила отталкивания между отдельными молекулами увеличится в:

Во сколько же раз в этом случае возрастёт давление газа? Чтобы правильно ответить на этот вопрос, вспомним, что же такое давление. Это величина усилия на единицу площади.

После сжатия, как мы определили, усилие каждой отдельной газовой молекулы на внутреннюю поверхность цилиндра увеличилось в <куб. кор из n>^ 2 раз. Но, помимо этого, увеличилось и количество молекул, оказывающих давление на ту же самую площадь внутренней поверхности цилиндра (см. рис. 5).

Рис. 5. При сжатии газа увеличивается количество молекул,

оказывающих давление на единицу площади.

Допустим, что если до сжатия на «единичную» площадь оказывало давление a× a молекул, то, как абсолютно очевидно, после сжатия газа в n раз число этих молекул стало <куб. кор. из n> a × <куб. кор. из n> a = <куб. кор. из n>^ 2 a^ 2 . То есть количество газовых молекул, оказывающих давление на «единичную» площадь, увеличилось в ^ 2 раз.

Если количество молекул, оказывающих давление на единицу площади поверхности, увеличилось в ^ 2 раз, и сила давления каждой молекулы на поверхность тоже увеличилось в ^ 2 раз, то давление газа при его сжатии в n раз увеличивается в ^ 2 × <куб.кор. из n>^ 2 = <куб.кор. из n>^ 4 = n ^<4/ 3> раз.

Таким образом, используя простейшие математические операции и логику, мы получаем показатель адиабаты для одноатомных идеальных газов, равный 4/3.

Как видим, он не соответствует общепринятому на сегодня показателю адиабаты для идеальных одноатомных газов, равному 5/3. Значит, выводы поспешны и не соответствуют истине? Вовсе нет. Ответ на вопрос, какая теория – молекулярно-кинетическая или электромагнитная более адекватно и более точно описывает реальное состояние газовых сред, могут дать только натурные эксперименты. Дело в том, что результаты прямого измерения показателя адиабаты для инертных газов вовсе не соответствуют теоретическим выкладкам, полученным из количества степеней свободы.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Адиабатный процесс. Изопроцессы в термодинамике

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы будем работать с уже известными нам физическими понятиями, но в несколько иной области применения. А именно с изопроцессами в термодинамике. Мы рассмотрим, какие изменения в первый закон термодинамики (закон сохранения энергии в тепловых процессах) внесут протекания этих самых процессов при неизменном макроскопическом параметре газа. Также мы рассмотрим новый, ранее неизвестный процесс – адиабатный.

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Адиабатный процесс, его суть и и формулы

Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Связь с первым началом термодинамики

Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении. Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю. Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Следствие из первого начала термодинамики для адиабатического процесса

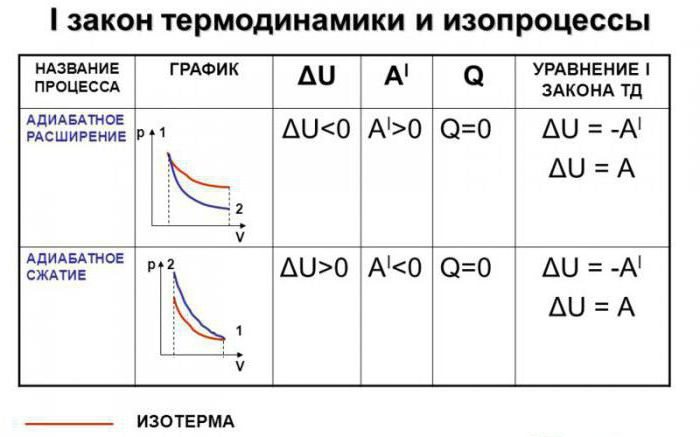
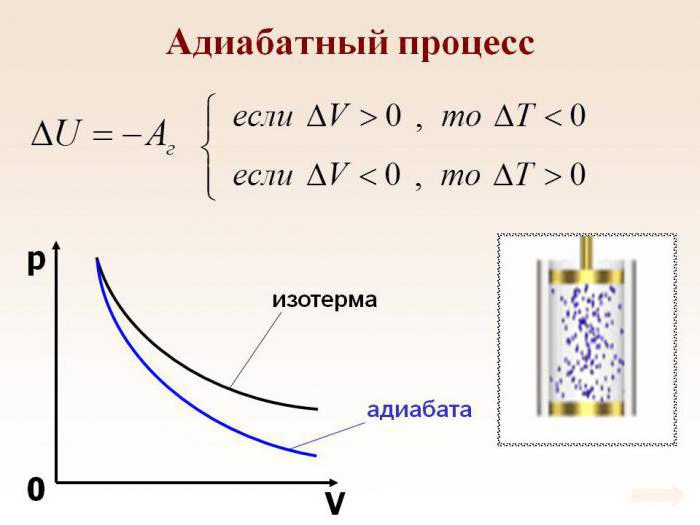
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования. Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения. Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Видео:Адиабатный процесс. Практическая часть. 10 классСкачать

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Видео:Цикл, состоящий из изотермы, изобары и адиабатыСкачать

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю. Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен. В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона. Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Видео:ЕГЭ Физика 2020.Адиабатный процесс.НЕстандартная С-шка #2Скачать

Примеры адиабатных процессов

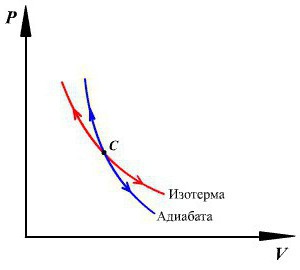
Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике. Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов. Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.