Уравнение адиабатного процесса связывающее давление и объем (4 видео)

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Содержание

Кратко об идеальном газе
Что это адиабатический процесс?
Уравнения Пуассона для адиабатического процесса
Пример задачи
Основы теплотехники
Термодинамические процессы
Изохорный процесс
Изобарный процесс
Изотермический процесс
Адиабатный процесс
Политропный процесс
Экспериментальное определение постоянной адиабаты
📺 Видео

Видео:Адиабатный процесс. 10 класс.Скачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Что это адиабатический процесс?

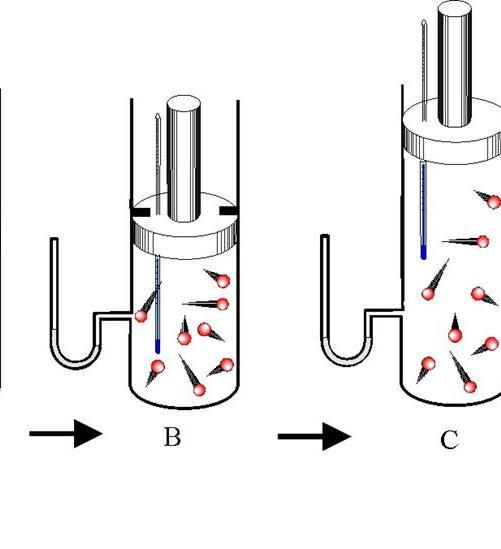
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

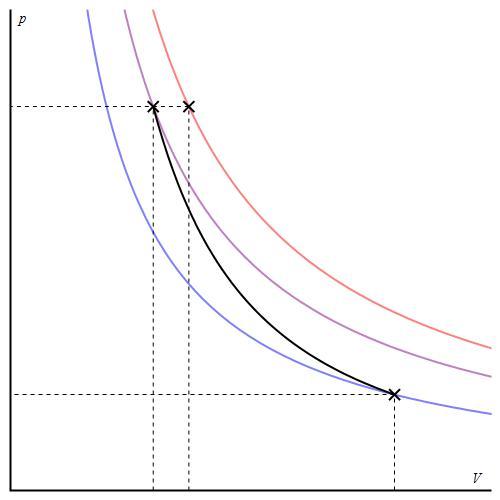
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

Видео:Изопроцессы, Адиабатный процесс.Скачать

Основы теплотехники

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Термодинамические процессы

Как упоминалось в предыдущей статье, термодинамическим процессом называют изменение состояния системы, в результате которого хотя бы один из ее параметров (температура, объем или давление) изменяет свое значение. Впрочем, если учесть, что все параметры термодинамической системы неразрывно взаимосвязаны, то изменение любого из них неизбежно влечет изменение хотя бы одного (в идеале) или нескольких (в реальности) параметров. В общем случае можно сказать, что термодинамический процесс связан с нарушением равновесия системы, и если система находится в равновесном состоянии, то никаких термодинамических процессов в ней протекать не может.

Равновесное состояние системы — понятие абстрактное, поскольку невозможно изолировать что-либо материальное от окружающего мира, поэтому в любой реальной системе неизбежно протекают разнообразные термодинамические процессы. При этом в некоторых системах могут иметь место настолько медленные, почти незаметные изменения, что связанные с ними процессы можно условно считать состоящими из последовательности равновесных состояний системы. Такие процессы называют равновесными или квазистатическими .
Еще один возможный сценарий последовательных изменений в системе, после которых она возвращается к исходному состоянию, называют круговым процессом или циклом . Понятия равновесного и кругового процесса лежат в основе многих теоретических выводов и прикладных приемов термодинамики.

Изучение термодинамического процесса заключается в определении работы, совершенной в данном процессе, изменения внутренней энергии, количества теплоты, а также в установлении связи между отдельными величинами, характеризующими состояние газа.

Из всех возможных термодинамических процессов наибольший интерес представляют изохорный , изобарный , изотермический , адиабатный и политропный процессы.

Изохорный процесс

Изохорным называют термодинамический процесс, протекающий при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
Изменение параметров газа в изохорном процессе описывает закон Шарля: p₁/T₁ = p₂/T₂ , или в общем случае:

Давление газа на стенки сосуда прямо пропорционально абсолютной температуре газа.

Так как в изохорном процессе изменение объема dV равно нулю, то можно сделать вывод, что вся подведенная к газу теплота расходуется на изменение внутренней энергии газа (никакая работа не совершается) .

Изобарный процесс

Изобарным называют термодинамический процесс, протекающий при постоянном давлении. Такой процесс можно осуществить, поместив газ в плотный цилиндр с подвижным поршнем, на который действует постоянная внешняя сила при отводе и подводе теплоты.
При изменении температуры газа поршень перемещается в ту или иную сторону; при этом объем газа изменяется в соответствии с законом Гей-Люссака:

Это означает, что в изобарном процессе объем занимаемый газом, прямо пропорционален температуре.
Можно сделать вывод, что изменение температуры в этом процессе неизбежно приведет к изменению внутренней энергии газа, а изменение объема связано с выполнением работы, т. е. при изобарном процессе часть тепловой энергии тратится на изменение внутренней энергии газа, а другая часть – на выполнение газом работы по преодолению действия внешних сил. При этом соотношение между затратами теплоты на увеличение внутренней энергии и на выполнение работы зависит от теплоемкости газа.

Изотермический процесс

Изотермическим называют термодинамический процесс, протекающий при неизменной температуре.
Практически осуществить изотермический процесс с газом очень трудно. Ведь необходимо соблюсти условие, чтобы в процессе сжатия или расширения газ успевал обмениваться температурой с окружающей средой, поддерживая собственную температуру постоянной.
Изотермический процесс описывается законом Бойля-Мариотта: pV = const , т. е. при постоянной температуре величина давления газа обратно пропорциональна его объему.

Очевидно, что при изотермическом процессе внутренняя энергия газа не изменяется, поскольку его температура постоянна.
Чтобы выполнялось условие постоянства температуры газа, от него необходимо отводить теплоту, эквивалентную работе, затраченной на сжатие:

Используя уравнение состояния газа, проделав ряд преобразований и подстановок, можно сделать вывод, что работа газа при изотермическом процессе определяется выражением:

Адиабатный процесс

Адиабатным называют термодинамический процесс, протекающий без теплообмена рабочего тела с окружающей средой. Подобно изотермическому, осуществить на практике адиабатный процесс очень сложно. Такой процесс может протекать с рабочим телом, помещенным в сосуд, например, цилиндр с поршнем, окруженный высококачественным теплоизолирующим материалом.
Но какой бы качественный теплоизолятор мы не применяли в данном случае, некоторым, пусть даже ничтожно малым, количеством теплоты рабочее тело и окружающая среда неизбежно будут обмениваться.
Поэтому на практике можно создать лишь приближенную модель адиабатного процесса. Тем не менее, многие термодинамические процессы, осуществляемые в теплотехнике, протекают настолько быстро, что рабочее тело и среда не успевают обмениваться теплотой, поэтому с некоторой степенью погрешности такие процессы можно рассматривать как адиабатные.

Для вывода уравнения, связывающего давление и объем 1 кг газа в адиабатном процессе, запишем уравнение первого закона термодинамики:

Поскольку для адиабатного процесса теплопередача dq равна нулю, а изменение внутренней энергии есть функция теплопроводности от температуры: du = c_vdT , то можно записать:

Продифференцировав уравнение Клапейрона pv = RT , получим:

Выразим отсюда dT и подставим в уравнение (3) . После перегруппировки и преобразований получим:

С учетом уравнения Майера R = c_p – c_v последнее выражение можно переписать в виде:

Разделив полученное выражение на c_v и обозначив отношение c_p/c_v буквой k , после интегрирования уравнения (4) получим (при k = const) :

ln vk + ln p = const или ln pvk = const или pvk = const .

Полученное уравнение является уравнением адиабатного процесса, в котором k – показатель адиабаты.
Если предположить, что объемная теплоемкость c_v является величиной постоянной, т. е. c_v = const , то работу адиабатного процесса можно представить в виде формулы (приводится без вывода) :

Политропный процесс

В отличие от рассмотренных выше термодинамических процессов, когда какой-либо из параметров газа оставался неизменным, политропный процесс характеризуется возможностью изменения любого из основных параметров газа. Все рассмотренные выше термодинамические процессы являются частными случаями политропных процессов.
Общее уравнение политропного процесса имеет вид pv n = const , где n – показатель политропы — постоянная для данного процесса величина, которая может принимать значения от — ∞ до + ∞ .

Очевидно, что придавая показателю политропы определенные значения, можно получить тот или иной термодинамический процесс – изохорный, изобарный, изотермический или адиабатный.
Так, если принять n = 0 , получим p = const – изобарный процесс, если принять n = 1 , получим изотермический процесс, описываемый зависимостью pv = const ; при n = k процесс является адиабатным, а при n равном — ∞ или + ∞ . мы получим изохорный процесс.

Так как уравнение политропы по своему содержанию аналогично уравнению адиабатного процесса, то формулы, устанавливающие связь между параметрами политропного процесса будут аналогичны таковым для адиабатного процесса с той лишь разницей, что показатель адиабаты k нужно заменить на показатель политропы n .
Тогда:

Работа газа при политропном процессе может быть определена по формуле:

Теплоемкость при политропном процессе (приводится без вывода) :

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники»
(в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Экспериментальное определение постоянной адиабаты

Лабораторная работа 4

Экспериментальное определение постоянной адиабаты

Изучить закономерности адиабатного процесса. Освоить метод определения отношения удельных теплоемкостей воздуха.

Приборы и принадлежности

Закрытый стеклянный сосуд с краном. Манометр. Поршневой насос. Зажим.

Любые процессы, протекающие в газах, подчиняются первому закону (началу) термодинамики, являющемуся по — существу законом сохранения и превращения энергии:

, (1)

где – элементарное количество теплоты, получаемое газом;

– приращение внутренней энергии газа;

– элементарная работа, совершаемая газом.

Совершаемая газом работа определяется выражением:

, (2)

где p – давление газа;

dV – приращение объема, занимаемого газом.

Внутренняя энергия идеального газа — это суммарная кинетическая энергия поступательного и вращательного движения всех его молекул. Изменение внутренней энергии однозначно связано с изменением температуры:

, (3)

где м и m – соответственно молярная масса и масса вещества;

R= 8.31 — универсальная газовая постоянная;

dT – изменение температуры газа;

i – число степеней свободы молекул (число независимых координат, задающих изменение положения молекулы в пространстве при поступательном движении и вращении). Поскольку вращение атома вокруг собственной оси не изменяет его положения в пространстве, то для одноатомных молекул i = 3, для двухатомных i = 5, для трехатомных и более i = 6.

Количество теплоты получаемое (дQ > 0) или отдаваемое (дQ 0), а при быстром расширении – охлаждаются;

2) работа при адиабатном расширении газа (дA>0) совершается за счет уменьшения его внутренней энергии (dU CV, поэтому г >1.

На рисунке 1 приведен график адиабатного процесса (адиабата) и для сравнения – график изотермического процесса (изотерма). Поскольку в уравнении изотермы объем в 1-й степени, то и давление изменяется менее резко.

Как и сами теплоемкости, их отношение для чистых газов может быть рассчитано теоретически:

. (21)

В других случаях величину г определяют опытным путем.

III. Теория эксперимента

Возьмем стеклянный сосуд, оборудованный манометром и соединяющийся посредством крана с атмосферой или насосом. Пусть первоначально в сосуде было атмосферное давление Ро. Если с помощью насоса быстро накачать в сосуд некоторое количество воздуха и закрыть кран, то в результате адиабатного сжатия температура воздуха в сосуде повысится, и устойчивая разность уровней воды в манометре h1 установится тогда, когда в результате теплообмена температура воздуха в сосуде сравняется с температурой окружающей среды Т0.

Это состояние газа назовем первым и будем характеризовать давлением Р1 и температурой Т1. Из предыдущего ясно, что

Если теперь открыть кран, то воздух будет быстро выходить из сосуда, пока его давление не сравняется с атмосферным Р0 . Поскольку расширение газа можно считать адиабатным, то температура снизится до Т2. Назовем это вторым состоянием с параметрами Р2 и Т2. При этом Р2 = Р0.

Если сразу, как только давление воздуха в сосуде сравняется с атмосферным, снова закрыть кран, то давление газа в сосуде будет возрастать в результате нагрева от окружающего воздуха. Окончательная разность уровней жидкости в манометре h2 установится при температуре в сосуде, равной температуре окружающего воздуха Т0. Это будет третьим состоянием газа в сосуде:

К процессу адиабатного расширения, т. е. к переходу из состояния 1 в состояние 2, может быть применен закон Пуассона (20), который для двух состояний записывается в следующей формуле:

. (24)

Так как переход из состояния 2 в состояние 3 происходит без изменения объема (изохорический процесс), то, применяя закон Шарля, получим:

. (25)

Из уравнений (24,25) с учетом условий (22,23)получаем:

Так как и — величины малые по сравнению с единицей, то разлагая оба двучлена по биному Ньютона, получим в первом порядке приближения:

, откуда

и . (26)

Прибор состоит из стеклянного герметически закупоренного баллона А (рис. 2). Сквозь пробку баллона проходят три трубки. Они соединяются с водяным манометром М. Вторая – с краном К1 для быстрого выпуска и впуска воздуха. Третья подведена к насосу. Кроме того, имеется зажим К на трубе, ведущий к насосу.

Рис. 2. Прибор для определения постоянной адиабаты

Результаты измерений разностей уровней в коленах манометра

Обработка результатов измерений

Вычислить г для каждого измерения по формуле Определить среднее значение абсолютной погрешности . Подсчитать относительную погрешность:

Записать окончательный результат в виде:

Вопросы для подготовки к отчету по работе

Какой процесс называется адиабатным? Каким путем осуществляются адиабатные процессы? Запишите уравнение первого начала термодинамики для адиабатного процесса. Почему Ср больше ? Что такое внутренняя энергия газа? Изобразите графически изотермический и адиабатный процессы. Что происходит с температурой газа при адиабатном сжатии? Где на практике осуществляются адиабатные процессы? Какой процесс называется круговым? Чему равна работа при адиабатном изменении объема газа?

В каком случае и почему адиабатный процесс нужно проводить быстро? Дайте определение удельной теплоемкости при постоянном давлении. В каких единицах измеряется молярная теплоемкость при постоянном объеме? Что происходит с температурой газа при адиабатном расширении? Какой газ называют идеальным? Чему равна внутренняя энергия одного моля газа? Почему отношение теплоемкостей больше единицы? Сравните полученный Вами результат с табличным и объясните, почему они не совпадают? Как уравнение Пуассона связывает давление и объем при адиабатном процессе? Дайте описание установки для определения отношения теплоемкостей.

Можно ли считать расширение и сжатие горючей смеси в двигателях внутреннего сгорания адиабатным процессом? Пояснить. Как уравнение Пуассона связывает температуру и давление при адиабатном процессе? Как связаны между собой молярная и удельная теплоемкости при постоянном объеме? Что называется числом степеней свободы? Вычислите внутреннюю энергию 1 моля воздуха при 270 С. Вычислите теоретически отношение теплоемкостей воздуха. Запишите первое начало термодинамики для адиабатного сжатия. Вычислите молярную теплоемкость воздуха при постоянном объеме. Изобразите графически адиабатный процесс. Почему при адиабатном расширении газа его температура понижается?