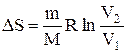Уравнение адиабатического процесса в координатах

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Адиабатический процесс | Все его важные концепции и графические кривые

Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Тема обсуждения: адиабатический процесс.

• Определение адиабатического процесса
• Примеры адиабатических процессов
• Формула адиабатического процесса
• Вывод адиабатического процесса
• Выполненная работа адиабатического процесса
• Обратимый адиабатический процесс и Необратимыйадиабатический процесс
• Адиабатический график

Видео:Адиабатный процесс. 10 класс.Скачать

Определение адиабатического процесса

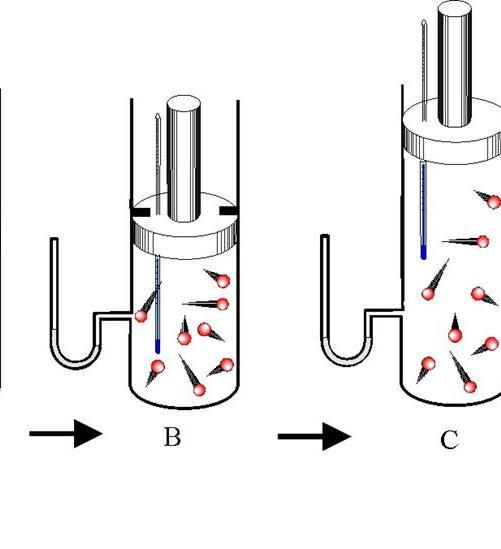
Соблюдая первый закон термодинамики, процесс, происходящий при расширении или сжатии, когда нет теплообмена от системы к окружающей среде, может быть известен как адиабатический процесс. В отличие от изотермического процесса, адиабатический процесс передает энергию окружающей среде в виде работы. Это может быть как обратимый, так и необратимый процесс.

В действительности, идеально адиабатический процесс никогда не может быть получен, поскольку ни один физический процесс не может происходить самопроизвольно, а система не может быть идеально изолирована.

Следуя первому закону термодинамики, который гласит, что когда энергия (как работа, тепло или материя) переходит в систему или из нее, внутренняя энергия системы изменяется в соответствии с законом сохранения энергии, где E можно обозначить как внутренняя энергия, а Q — это тепло, добавленное к системе, а W — проделанная работа.

ΔE=Q—W

Для адиабатического процесса, в котором нет теплообмена,

ΔE= —W

Условия, необходимые для протекания адиабатического процесса:

• Система должна быть полностью изолирована от окружающей среды.
• Чтобы передача тепла происходила за достаточное время, процесс должен выполняться быстро.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Адиабатический процесс Пример

1. Процесс расширения в двигателе внутреннего сгорания среди горячих газов.
2. Квантово-механический аналог осциллятора, классически известного как квантовый гармонический осциллятор.
3. Сжиженные газы в системе охлаждения.
4. Воздух, выпущенный из пневматической шины, является наиболее важным и частым случаем адиабатического процесса.
5. Лед, хранящийся в морозильной камере, следует принципам, согласно которым тепло не передается в окружающую среду и обратно.
6. Турбины, использующие тепло в качестве среды для создания работы, считаются отличным примером, поскольку они снижают эффективность системы, поскольку тепло теряется в окружающую среду.

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Формула адиабатического процесса

Выражение адиабатического процесса в математических терминах может быть дано следующим образом:

ΔQ = 0

ΔU = -W, (так как в системе отсутствует тепловой поток)

Рассмотрим систему, в которой выполняется исключение теплового и рабочего взаимодействий в стационарном адиабатическом процессе. Единственные энергетические взаимодействия — это граничная работа системы в ее окружении.

Идеальный газ

Количество тепловой энергии на единицу температуры, недоступной для выполнения определенной работы, можно определить как энтропию системы. Спекулятивный газ, который представляет собой беспорядочное движение точечных частиц, подверженных межчастичным молекулярным взаимодействиям, идеален.

Молярная форма формулы идеального газа определяется следующим образом:

Уравнение адиабатического процесса можно обозначить как:

PVY = постоянный

Для обратимого адиабатического процесса

• P 1-Y T Y = постоянная,
• VT F / 2 = постоянная,
• TV Y-1 = константа. (T = абсолютная температура)

Этот процесс также известен как изэнтропический процесс, идеализированный термодинамический процесс, включающий передачу работы без трения и адиабатический. В этом обратимом процессе нет передачи тепла или работы.

Видео:Адиабатный процесс. Практическая часть. 10 классСкачать

Вывод адиабатического процесса

Изменение внутренней энергии dU в системе сделать работу dВт плюс добавленное тепло dQ с ним можно связать первый закон термодинамики, с помощью которого можно вывести адиабатический процесс.

Добавление тепла увеличивает количество энергии U определение удельной теплоемкости как количества тепла, добавляемого на единицу повышения температуры на 1 моль вещества.

(n — количество молей), Следовательно:

Получено из закон идеального газа,

Уравнение слияния 1 и 2,

Для постоянного давления C_p, добавляется тепло и,

γ — это удельная теплоемкость

Используя концепции интеграции и дифференциации, мы пришли к следующему:

Это уравнение, приведенное выше, становится реальным для данного идеального газа, который содержит адиабатический процесс.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Адиабатический процесс Работа выполнена.

Для давления P и площадь поперечного сечения A перемещение на небольшое расстояние dx, действующая сила будет определяться следующим образом:

А проделанную работу в системе можно записать так:

Чистая работа, произведенная для расширения газа из объема газа V_i к V_f (от начального до финального) будут представлены как

W = площадь ABDC от графика, построенного как имеет место адиабатический процесс. Условия, которые необходимо соблюдать, связаны с примером совершенно непроводящего поршневого цилиндра с одной граммовой молекулой идеального газа. Емкость баллона должна быть изготовлена ​​из изоляционного материала, а кривая на графике должна быть более резкой.

Принимая во внимание, что в аналитическом методе для вывода работы, выполненной в системе, будет следующее:

Изначально для адиабатического изменения можно предположить:

Который может быть,

Из (1),

Принимая T₁ и т₂ как начальная и конечная температуры газа соответственно,

Используя это в уравнении (2),

Тепло, необходимое в процессе расширения для выполнения работы:

Поскольку R — универсальная газовая постоянная, и во время адиабатического расширения совершаемая работа прямо пропорциональна снижению температуры, в то время как работа, совершаемая во время адиабатического сжатия, отрицательна.

Это можно представить как работа, выполненная в адиабатическом процессе.

И тепло, выделяемое во время процесса:

Видео:Урок 162. Построение графиков изопроцессов в различных координатахСкачать

Адиабатический график

Математическое представление кривой адиабатического расширения представлено следующим образом:

P, V, T — давление, объем и температура процесса. Рассматривая начальные условия системы как P₁, V₁, и т₁, также определяя финальную стадию как P₂, V₂, и т₂ соответственно, графическая диаграмма PV построена по существу для движения поршневого цилиндра, адиабатически нагретого от начального до конечного состояния для XNUMX кг воздуха.

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Адиабатическая энтропия, адиабатическое сжатие и расширение

Газ, которому позволено свободно расширяться без передачи ему внешней энергии от более высокого давления к более низкому, будет по существу охлаждаться по закону адиабатического расширения и сжатия. Точно так же газ нагреется, если его сжать с более низкой температуры до более значительной температуры без передачи энергии веществу.

• Посылка воздуха расширится, если давление окружающего воздуха уменьшится.
• На больших высотах наблюдается снижение температуры из-за уменьшения давления, поскольку они прямо пропорциональны в случае этого процесса.
• Энергия может использоваться либо для работы по расширению, либо для поддержания температуры процесса, но не для того и другого одновременно.

Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Обратимый адиабатический процесс

Процесс без трения, в котором энтропия системы остается постоянной, получил название обратимого или обратимого. изоэнтропический процесс. Это означает, что изменение энтропии постоянно. Внутренняя энергия эквивалентна работе, совершаемой в процессе расширения.

Поскольку нет теплопередачи,

Которое значит что,

Примеры обратимого изоэнтропического процесса можно найти в газовые турбины.

Видео:Решение графических задач на тему Газовые законыСкачать

Необратимый адиабатический процесс

Как следует из названия, процесс рассеяния внутреннего трения, приводящий к изменению энтропии системы во время расширения газов, является необратимым адиабатическим процессом.

Обычно это означает, что энтропия увеличивается по мере развития процесса, который не может быть выполнен в равновесии и не может быть отслежен до исходного состояния.

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Видео:Физика Изучение графиков изопроцессовСкачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Что это адиабатический процесс?

Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Изопроцессы, Адиабатный процесс.Скачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

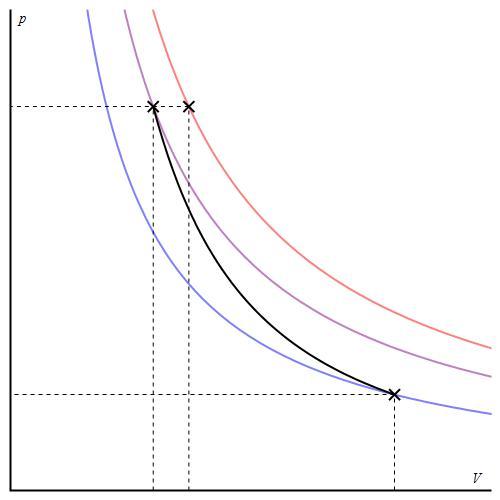
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:Лекция по физике №8. Распределение Больцмана. Теплоёмкость, Уравнение адиабатического процесса.Скачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

Видео:ЕГЭ Физика 2020.Адиабатный процесс.НЕстандартная С-шка #2Скачать

Адиабатический процесс. Политропный процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, адиабатическим процессом можно считать процесс в двигателях внутреннего сгорания(расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д.

Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что

dА=-dU, (2.6.1)
т.е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражение для произвольной массы газа перепишем уравнение в виде

. (2.6.2)

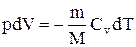
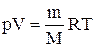
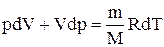
Продифференцировав уравнение состояния для идеального газа , получим

. (2.6.3)
Исключим из (2.6.2) и (2.6.3) температуру Т:

.
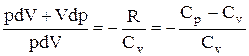
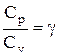
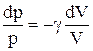
Разделив переменные и учитывая, что найдем

.

Интегрируя это уравнение в пределах от p₁ до р₂ и соответственно от V₁ до V₂, а затем потенцируя, придем к выражению

.

.

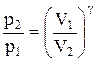
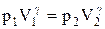
Так как состояния 1 и 2 выбраны произвольно, то можно записать

PV g =const. (2.6.4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из (2.6.4) с помощью уравнения Клапейрона-Менделеева:

,

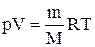
соответственно давление или объем:

(2.6.5)

. (2.6.6)

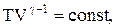
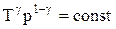
Эти выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

(2.6.7)
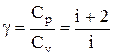
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, g =1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, g =1,4. Значения вычисленные по формуле (2.6.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабат а) в координатах р, V изображается гиперболой (рис. 2.6.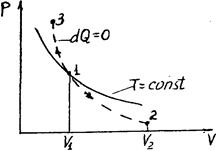1).

Рис. 2.6.1

На рисунке видно, что адиабата ( 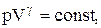) более крута, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Вычислим работу, совершаемую газом в адиабатическом процессе.
Запишем уравнение в виде

.

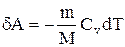
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до Т₂ и работа расширения идеального газа

. (2.6.8)

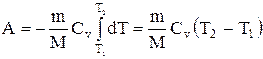
Применяя те же приемы, выражение (2.6.8) для работы при адиабатическом расширении можно преобразовать к виду

.

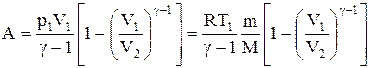
Работа, совершаемая газом при адиабатическом расширении 1-2 (определяется заштрихованной площадью, выполненной на рис. 61), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_v и С_p, в изотермическом процессе (dT=0) теплоемкость равна ±¥, в адиабатическом (dQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const), можно вывести уравнение политропы:

pV n =const, (2.6.9)
где 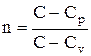— показатель политропы. Очевидно, что при С=0, n=gполучается уравнение адиабаты; при С=¥, n=l — уравнение изотермы; при С=С_p, n=0 — уравнение изобары, при С=С_v , n=±¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

2.7 Круговой процесс (цикл).
Обратимые и необратимые процессы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 2.7.1).

Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1-2) и сжатия (2-1) газа. Работа расширения (определяется площадью фигуры 1а2V₂V₁) положительна (dV > 0), работа сжатия (определяется площадью фигуры 2blV₁V₂2) отрицательна (dV 0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 2.7.1,а), если за цикл совершается отрицательная работа 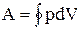0. (2.8.4)

Выражения (2.8.3) и (2.8.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (2.8.3) и (2.8.4) можно представить в виде неравенства Клаузиуса

DS 0, (2.8.5)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2.8.2), изменение энтропии

, (2.8.6)
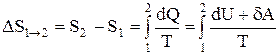
где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (2.8.6) определяет энтропию лишь с точностью до аддитивной постоянной.

Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (2.8.6), найдем изменение энтропии в процессах идеального газа. Так как

,

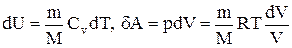
то ,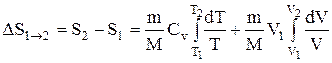

или 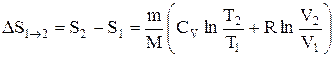, (2.8.7)

т.е. изменение энтропии 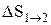идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1®2.

Так как для адиабатического процесса dQ=0, то DS=0 и, следовательно, S=const, т.е. адиабатический обратимый процесс протекает при постоянной энтропии. Из формулы (2.8.7) следует, что при изотермическом процессе (T₁=T₂)

при изохорном процессе (V₁ =V₂)

.

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему.

Более глубокий смысл энтропии вскрывается в статистической физике, энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S=kInW, (2.8.8)
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
Так как реальные процессы необратимы, то можно утверждать, что все
процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных к более вероятным.

Сопоставляя выражения (2.8.5) и (2.8.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.

📽️ Видео

Урок 31. Работа в термодинамике и адиабатический процесс.Скачать

Применение первого начала термодинамики к изопроцессамСкачать

Адиабатическое охлаждение.Скачать