Уравнение аддитивности или правило смесей (5 видео)

Правило смесей

Правило смесей — раздел Образование, Классификация композиционных материалов Так Как Свойства Км Определяются Свойствами Составляющих Его .

Так как свойства КМ определяются свойствами составляющих его матрицы и арматуры, то необходимо установить зависимость свойств КМ от концентрации (количества) этих составляющих.

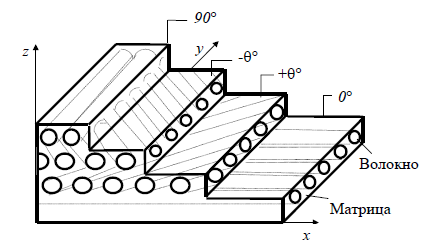
Рис.2.4. Диаграмма растяжения волокон (1), матрицы (3) и однонаправленного КМ (2)

Вернемся к модели однонаправленного трансверсально изотропного КМ и рассмотрим характер его деформации под действием растягивающей нагрузки, приложенной параллельно оси волокон (рис. 2.4).

Предположим, что матрица более пластична (e_м.пред>e_в.пред) и имеет меньший модуль упругости, чем волокна (модуль упругости характеризуется тангенсом угла наклона линейного участка кривой к оси деформаций).

В общем случае кривая 2 растяжения КМ должна состоять из трех участков: I – матрица и волокна деформируются упруго; II – матрица переходит в упругопластическое состояние, а волокна продолжают деформироваться упруго; III – оба компонента системы находятся в состоянии пластической деформации. В зависимости от свойств компонентов КМ участки II и III на кривой могут отсутствовать.

Примем, что прочность связи на границе раздела волокно-матрица достаточна для того, чтобы обеспечить совместную деформацию компонентов вплоть до разрушения, т.е. что e_в = e_м = e_к.

Поэтому сумма нагрузок, приходящихся на матрицу и волокна, равна внешней нагрузке, воспринимаемой КМ.

Тогда, используя уравнение. (2.6), предел прочности КМ σ_вк можно выразить в виде линейной функции от объемной доли волокон V_в:

(2.19)

– среднее значение предела прочности волокон при растяжении;

– напряжение в матрице в момент разрыва волокон (рис. 2.3);

V_м, V_в – объемная доля матрицы и волокна в КМ, соответственно.

Следует подчеркнуть, что d_м – это не предел прочности матрицы, а напряжение, соответствующее такой ее деформации, которая равна предельной деформации волокон до разрушения e_в _пред. Чтобы определить d_м, нужно из точки С (рис. 2.4.), соответствующей относительной деформации разрушения волокон e_в, восстановить перпендикуляр. Ордината точки Д пересечения этой прямой с кривой 3 будет равна d_м. Для неупрочняющихся пластичных матриц d_м можно принять равной пределу текучести матрицы.

Уравнение (2.19) обычно называют уравнением смесей (правилом смесей) или уравнением (правилом) аддитивности.

На практике во многих случаях допущения, принятые для вывода этого уравнения, нарушаются. Волокна могут разрушаться не одновременно, а последовательно из-за наличия в них дефектов. Наиболее дефектные волокна разрушаются при малых напряжениях, далеких от предела прочности; волокна с меньшей дефектностью разрушаются при несколько больших напряжениях; а в целом прочность КМ будет меньше рассчитанной по правилу смесей. То же можно сказать, когда матрица имеет недостаточный запас пластичности, что приводит к появлению трещин на границе раздела и в теле матрицы и к преждевременному разрушению КМ в целом.

Однако возможны случаи, когда реальная прочность однонаправленного армированного материала оказывается выше, чем предсказывается правилом аддитивности. Например, если пластичная матрица армирована пластичными волокнами, то при растяжении КМ связь между волокнами и матрицей затрудняет образование шейки на волокнах. В результате волокна в КМ деформируются более равномерно, чем при их растяжении в чистом виде (без матрицы). В последнем случае после образования шейки вся дальнейшая деформация концентрируется в ней, вызывая быстрое разрушение. Таким образом, задержка в образовании шейки в конечном итоге увеличивает условный предел прочности волокон и композиции в целом. Тем не менее, уравнение (2.19) можно использовать для оценочных расчетов, так как во многих случаях (при условии получения КМ по оптимальным технологическим режимам) отклонение расчетных значений прочности от экспериментальных невелико.

Содержание

Основные прочностные характеристики
Как создают композиты
Материаловедение
Армированные композиты
Теория и практика
Пример создания композита
Рассуждения материаловеда-композитчика
Правило смесей
Модуль Юнга для композита
🌟 Видео

Видео:№22 из ОГЭ. Задачи на смеси и сплавы | Математика | TutorOnlineСкачать

Основные прочностные характеристики

Прочность и жесткость являются важнейшими характеристиками любого материала. При нагружении образца растяжением или сжатием в нем возникают нормальные напряжения σ и соответствующие им деформации ε, которые растут вплоть до разрушения материала. Предельное (максимальное) напряжение называют его прочностью. Связь между упругими напряжениями σ, действующими на тело, и деформациями ε, вызванными этими напряжениями, устанавливает закон Гука. Для одностороннего растяжения или сжатия изотропного тела, на которое действует только одна сила, закон Гука записывается в виде

Коэффициент пропорциональности Е называют модулем упругости, или модулем нормальной упругости, или модулем Юнга.

Оценки упругих характеристик КМ основываются на допущениях о жесткой связи между матрицей и волокнами, их совместной деформации и подчинении закону Гука [6].

Для простейшей модели КМ – системы жестко связанных и чередующихся изотропных стержней, обладающих характеристиками волокна, и матрицы – продольный модуль упругости Е_х (в направлении, продольном оси волокон) рассчитывается по уравнению аддитивности, или правилу смесей:

где E_в – модуль упругости волокон;

E_м – модуль упругости матрицы;

V_в – объемная доля волокон;

V_в – объемная доля матрицы.

Поперечный модуль упругости E_v (в направлении, перпендикулярном оси волокон) определяется из выражения

. (4)

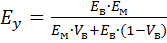
По аналогии с растяжением связь между касательными напряжениями τ и соответствующими упругими сдвиговыми деформациями γ можно записать в виде выражения:

где G – модуль упругости при сдвиге (модуль сдвига).

В однонаправленном КМ при совпадении оси х с направлением укладки волокон модули G_xv и G_xz характеризуют упругие сдвиги КМ в двух плоскостях ху и xz, параллельных волокнам. Правило аддитивности для КМ со сплошными волокнами можно представить следующим образом:

. (6)

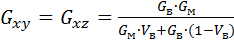
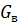
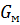
где – модуль сдвига волокон;

– модуль сдвига матрицы.

При одноосном растяжении изотропного материала наряду с увеличением его длины в направлении действия силы (например, по оси х) уменьшаются поперечные размеры вдоль двух других осей (у и х). Отношение относительных деформаций тела в поперечном ε_y и продольном ε_х направлениях называют коэффициентом Пуассона μ:

. (7)

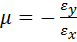
Величина μ_xy однонаправленного двухкомпонентного КМ по правилу смесей оценивается следующим образом:

, (8)

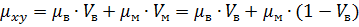
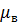
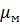
где – коэффициент Пуассона волокон;

– коэффициент Пуассона матрицы.

Следует отметить, что приведенные соотношения можно рассматривать только как приближенные, оценочные, поскольку модели расчета идеализированы. Технологические дефекты, неоднородность распределения волокон по объему КМ, разориентация и неоднородность свойств компонентов приводят к тому, что реальные характеристики армированных композиций отличаются от расчетных. Поэтому для паспортизации КМ обычно используют экспериментально определенные упругие константы.

Упругие свойства изотропных материалов хорошо описываются двумя константами Е и G, взаимосвязь между которыми соответствует уравнению

. (9)

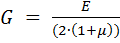
Приведенные соотношения хорошо описывают изотропные материалы, свойства которых во всех направлениях одинаковы. К таковым можно отнести дисперсно-наполненные полимеры, а также КМ на основе коротких или непрерывных волокон хаотичной структуры. Для волокнистых материалов всегда имеется определенная степень ориентации, определенная влиянием технологических факторов.

При нагружении какой-либо конструкции напряженно-деформированное состояние материала чаше всего становится неоднородным. При этом предоставляется возможность выявить главные (максимальные) напряжения, которые могут явиться причиной ее разрушения. Например, в случае трубы, находящейся под внутренним или внешним давлением, окружные напряжения в два раза превосходят осевые напряжения, то есть половина толщины изотропного материала с точки зрения осевых напряжений неэффективна. Неоднородность поля напряжений может быть и существенно выше. Для оболочек с открытым выходом (ружья, стволы гранатометов) соотношение радиальных и осевых напряжений достигает от 8 до 10 и более. В этих случаях следует воспользоваться замечательной способностью волокнистых материалов, которые можно ориентировать в матрице в соответствии с распределением главных эксплуатационных напряжений [7].

5 Определение упругих характеристик однонаправленного слоя

Изучение механического поведения композиционных материалов проводится на двух уровнях абстрагирования. Первый уровень, называемый микромеханикой, включает тонкие детали структуры композита на уровне размеров волокна, которое помещено в матрицу. Основным результатом решения задачи в микромеханической постановке является вычисление эффективных модулей однонаправленного слоя, которые определяются как коэффициенты, связывающие усредненные по объему значения напряжений (компонент тензора напряжений) и деформаций (компонент тензора деформаций) при определенных граничных условиях.

Вычисление эффективных модулей композиционных материалов основано на понятии представительного элемента объема, то есть такого элемента, в котором все усредненные по объему компоненты напряжений и деформаций равны соответствующим величинам, вычисленным для рассматриваемого композита в целом. Как правило, микромеханика ограничивается вычислением эффективных модулей упругости и коэффициентов Пуассона однонаправленного композиционного слоя. Эти вычисления дают возможность дальнейшего аналитического исследования на новом уровне абстрагирования, а именно на уровне слоистого тела. При этом реальный неоднородный материал рассматривается как однородное анизотропное тело, состоящее из однонаправленных слоев, ориентированных под разными углами (рисунок 5).

Рисунок 5 – Волокнистый композиционный материал с укладкой
слоев: 90°, -θ, θ, 0°

Слой – основной элемент в КМ, состоящий из погруженных в матрицу однонаправленных волокон. Следовательно, можно связать упругие и прочностные свойства однонаправленного слоя с соответствующими свойствами компонентов. Таким образом, имеется возможность проектировать элементы конструкций из волокнистых КМ, зная конструктивные требования к конструкции и свойства компонентов КМ.

При определении упругих постоянных однонаправленного слоя по известным упругим характеристикам волокон и связующего необходимо рассмотреть напряженно-деформированное состояние последних при нагружении слоя вдоль армирования, поперек и при сдвиге. Совместная работа волокна и связующего, обладающих различными упругими характеристиками, представляет собой сложную математическую задачу. Для определения напряжений и деформаций в компонентах КМ используют физические и математические модели как самих компонентов, так и модели их совместной работы.

Для упрощения расчетов вводится ряд допущений:

1) компоненты композиционного материала являются однородными и линейно-упругими материалами;

2) связующее является изотропным, а волокна могут быть изотропными или трансверсально-изотропными;

3) армирующие волокна являются прямыми и параллельными;

4) армирующие волокна распределены равномерно и имеют одинаковое сечение.

Сама модель их совместной работы предполагает, что между арматурой и связующим существует жесткое сцепление, то есть отсутствует скольжение. Поры как в арматуре и связующем, так и на поверхности их раздела отсутствуют.

Для определения напряжений в компонентах однонаправленного слоя в качестве расчетной модели будем пользоваться повторяющимся элементом структуры материала. Периодически повторяющийся элемент представляет собой типичную модель, применяемую в микромеханике для определения механических свойств КМ. На рисунке 6 показаны модели, которые используются для определения упругих свойств композитов на основе методов сопротивления материалов.

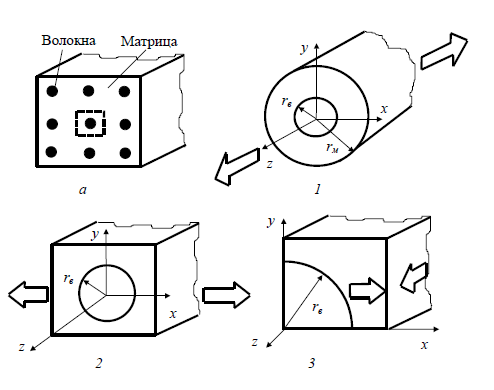
Рисунок 6 – Представительный объем композиционного материала (a) и
повторяющиеся элементы однонаправленного слоя для определения
продольного модуля упругости (1), поперечного модуля упругости (2) и
модуля сдвига (3)

В этой модели выделяются три элемента: первый – для определения поля внутренних напряжений при нагружении вдоль волокон, второй – для определения напряжений при нагружении поперек волокон, третий – для определения напряжений при сдвиге. Определение поля внутренних напряжений в волокне и связующем при различных видах нагружения представляет большие математические трудности. В инженерных расчетах, как правило, используют упрощенные модели, базирующиеся на методах сопротивления материалов.

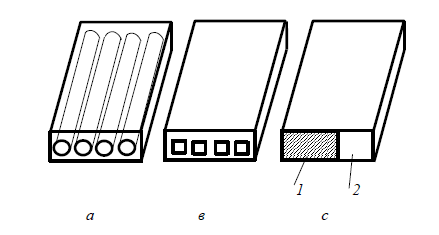
В качестве упрощенной модели используется однонаправленный слой, состоящий из объема, занятого армирующими волокнами, и объема, занятого матрицей (рисунок 7).

1 – объем, занятый волокном; 2 – объем, занятый матрицей

Рисунок 7 – Модели однонаправленного слоя с круглыми (а) и эквивалентными им по площади прямоугольными волокнами (в), с – упрощенная модель однонаправленного слоя для определения упругих свойств

Возможность в этой модели пренебречь влиянием коэффициентов Пуассона волокна и матрицы, геометрической формой поперечного сечения армирующих волокон при определении эффективных модулей упругости однонаправленного слоя позволяет существенно упростить расчеты [8].

Дата добавления: 2016-01-26 ; просмотров: 3503 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Задачи на смеси. Нахождение состава конечной смеси (в ) с составлением системы уравнений.Скачать

Как создают композиты

Сегодня наука многое знает о строении материалов и их свойствах, знает «привычки» и «вкусы» различных материалов, и это позволяет улучшать известные и создавать новые материалы не вслепую, не наудачу, а целенаправленно. Наглядно это можно продемонстрировать на том, как создают композиты. Плавка метала для создания композита

Видео:Основы теплотехники. Теплоёмкость газов и газовых смесей. Уравнение МайераСкачать

Материаловедение

Материаловедение изучает общие закономерности создания материалов, устанавливает связи между строением, составом и свойствами материалов. Используя эти закономерности и связи, разработчики новых материалов намечают области поиска и движутся к своей цели осознанно, не блуждая в потемках, как Палисси, создавая французский фарфор, (подробнее: История создания французского фарфора).

Пути, ведущие к цели, сегодня уже достаточно хорошо освещены, на некоторых из них установлены мощные прожекторы, на других повешены маленькие фонарики. По ярко освещенным дорогам можно двигаться быстро, по слабо освещенным — медленнее, преодолевая бугры и пробираясь сквозь заросли, но направление выдерживать можно достаточно четко.

Вот по таким дорогам и движутся сегодня отряды материаловедов. А кто-то открывает новые пути, и им необходима интуиция Палисси. Как же сегодня создаются композиты. Это неверное утверждение, что метод проб и ошибок уже не используется вообще. Используется. Но сравнительно мало.

Видео:Объемные отношения газов при химических реакциях. 8 класс.Скачать

Армированные композиты

Армированным композитам повезло больше, чем другим материалам. К тому времени, когда созрела мысль о необходимости их разработки, уже существовала теория анизотропных сред, которая позволяла предсказывать заранее свойства композитов по известным свойствам компонентов.

Если древние металлурги, добавляя в расплавленное железо вещество, не знали, как оно повлияет на свойства стали, (подробнее: Тайна булата) то создатели армированных композитов четко знают, что они должны получить, вводя определенный вид волокон в определенную матрицу.

И могут предсказать свойства будущего материала не только качественно, но и количественно. Потому что они опираются на прочный теоретический фундамент.

Видео:8. Разделение смесей (неоднородных)Скачать

Теория и практика

Это не означает, что на практике всегда получается то, что предсказывает теория. К сожалению, полное согласие теории с практикой наблюдается далеко не всегда. Теория, как правило, строится для каких-то определенных моделей, которые отражают главные особенности реальных композитов. Главные, но не все.

Все она просто не может учесть, потому что их очень много, и попытка учесть все приводит к такому усложнению, что пользоваться такой теорией просто невозможно. Поэтому каждая теория справедлива в тех рамках, которые оговорены при ее построении. А реальные материалы об этих рамках ничего не знают.

И если их поведение в эти рамки не укладывается, то нужно винить не теорию, а тех, кто ее применяет там, где применять нельзя. Но для большей части армированных композитов теория армированных сред позволяет достаточно надежно оценивать свойства, которые могут быть достигнуты, то есть дает ориентир, к которому следует стремиться.

Эта теория в общем виде довольно сложна, и чтобы ее понять, нужно знать специальные разделы высшей математики. Мы не будем их касаться, а чтобы все-таки получить представление о том, как можно заранее прогнозировать свойства композитов, рассмотрим простейший пример, для понимания которого вполне достаточно знаний среднего пятиклассника.

Видео:Урок 12. Задача на смеси. Практика. Химия 11 классСкачать

Пример создания композита

Требуется создать композит на основе алюминия с прочностью 1000 МПа и модулем Юнга 200 ГПа. Достаточно иметь эту прочность только в одном направлении, в остальных допустима прочность на уровне алюминия. Плотность композита не должна превышать плотности алюминиевых сплавов. Алюминий как основа создания композита

Если задачу перефразировать, получится следующее: требуется создать материал на основе алюминия, обладающий прочностью и жесткостью хорошей легированной стали и сохраняющий при этом весовые характеристики алюминия.

Традиционными металлургическими методами (легированием, термической обработкой, пластической деформацией) это сделать невозможно. Прочность чистого алюминия составляет 120—150 МПа, алюминиевых сплавов — до 500—700 МПа. Большего добиться не удается.

Модуль Юнга алюминия и его сплавов примерно 70 ГПа, причем легирование, термообработка и пластическая деформация практически не влияют на его величину. А нам нужно увеличить его почти втрое.

Алюминий относится к числу легких металлов (плотность 2700 кг/м 3 ), и если осуществлять легирование более тяжелыми элементами, чем сам алюминий, это приведет к увеличению плотности и не позволит выполнить поставленные требования.

Рассуждения материаловеда-композитчика

Проследим за ходом рассуждений материаловеда-композитчика. Для него ясно, что задача должна решаться путем создания композиционного материала. Поскольку требуется обеспечить прочность только в одном направлении, нужно создавать армированный материал, в котором армирующие волокна уложены параллельно друг другу.

Вдоль их оси и будет обеспечена максимальная прочность и жесткость. Вопрос в том, какие волокна использовать и сколько их ввести? Ясно, что в качестве арматуры нужны волокна с максимальными значениями прочности и жесткости. Но только этими показателями ограничиваться нельзя.

Например, вольфрамовые волокна, хотя и обладают высокими механическими характеристиками, имеют большую плотность, и, используя их в качестве арматуры, мы заведомо не сможем выполнить требование, касающееся плотности разрабатываемого композита. По той же причине следует отказаться от применения стальных проволок и волокон карбида кремния.

Нитевидные кристаллы, (подробнее: Металлические усы) могли бы помочь решить задачу, но, как мы уже знаем, их использование связано с большими технологическими трудностями и крупными материальными затратами. Пожалуй, наиболее целесообразно попробовать волокна бора и углерода.

Их применение не увеличит плотность композита по сравнению с алюминием (углеродные волокна даже уменьшат ее), а модуль упругости и прочность должны повыситься. Необходимо подсчитаем, сколько волокон нужно ввести, чтобы обеспечить заданные механические характеристики.

Сколько — это значит не сколько штук, а сколько процентов по объему должны занимать в композите волокна.

Правило смесей

Расчет здесь простой. Нужно применить правило аддитивности, т.е. воспользоваться правилом смесей. Раньше в четвертом-пятом классах решали задачи такого типа: килограмм карамелек стоит 1 рубль, а килограмм ирисок — 3 рубля. Сколько будет стоить килограмм смеси, составленной из двух килограммов карамелек и четырех килограммов ирисок?

Казалось бы, кому нужно знать стоимость килограмма этой злосчастной смеси, ведь ни одного нормального покупателя такой вопрос совершенно не волнует. Но оказалось, задачи о смесях на самом деле — очень нужная штука. Их нередко используют в разных технических расчетах и в частности при оценочных расчетах некоторых свойств композитов.

Например, прочность и жесткость композиционного материала в направлении армирования можно рассчитать точно так же, как стоимость одного килограмма смеси. Композит в первом приближении можно рассматривать как смесь матрицы и волокон. (Это можно сделать далеко не всегда, но в данном случае для оценочных расчетов — можно.)

Цена одного килограмма смеси определяется по простой формуле: Ц = Ц₁ N₁ + Ц₂ N₂. В этой формуле Ц₁ Ц₂ и Ц — цены карамелек, ирисок и смеси соответственно; N₁ — доля карамелек в смеси, N₂ — доля ирисок в смеси. При этом в сумме N₁ + N₂ = 1. В смеси, состоящей из 2кг карамелек и 4кг ирисок, доля карамелек N₁ = 2/(2+4) = 1/3, а доля ирисок N₂ = 4/(2+4) = 2/3.

В соответствии с приведенной формулой цена 1кг смеси из карамелек и ирисок составит: Ц = 1(руб/кг) 1/3 + 3(руб/кг) 2/3 = 2 1/3 (руб/кг).

Модуль Юнга для композита

По аналогичной формуле можно рассчитать модуль Юнга для композита в направлении укладки волокон: Е = E_M V_M +E_B V_B. Здесь E_M, E_B, Е — модули Юнга матрицы, (подробнее: Армированные композиты), волокон и композита соответственно; V_M, V_B — объемные доли матрицы и волокон в композите. Бронепластина как яркий пример применения композита

С учетом того, что V_M + V_B = 1, это выражение можно записать в виде: Е = E_M (1-V_B) + E_B V_B. Последней формулой воспользуемся для решения поставленной задачи. Нам нужно получить композит с модулем Юнга Е = 200 ГПа. Модуль Юнга алюминиевой матрицы E_M = 70 ГПа, средний модуль Юнга борных волокон E_B = 400 ГПа, а углеродных волокон E_B = 350 ГПа.

Следовательно, для композита, армированного борными волокнами, формула примет вид: 200=70 (1-V_B) + 400 V_B. Решая это уравнение относительно V_B, получим: V_B = 0,39 = 39 % (по объему). Для композита алюминий — углеродные волокна — 200 = 70(1-V_B) + 350V_B, откуда V_B = 0,46 = 46 % (по объему).

Таким образом, чтобы выполнить требование по жесткости, необходимо ввести в алюминий либо 39 % (по объему) борных волокон, либо 46 % (по объему) углеродных волокон. Прочность композита тоже может быть рассчитана по правилу смесей.

Если волокна менее пластичны, чем матрица (а у нас как раз такой случай), то прочность армированного материала в направлении укладки волокон приближенно оценивается формулой: (Ϭ_B)_к = (Ϭ_B)_в V_B + Ϭ_М (1-V_B) Здесь (Ϭ_B)_к и (Ϭ_B)_в — пределы прочности композита и волокон; Ϭ_М — величина, близкая к пределу текучести матрицы; V_B— объемная доля волокон. Нам нужно получить (Ϭ_B)_к = 1000 МПа.

Борные волокна в среднем имеют (Ϭ_B)_в = 3250 МПа, а углеродные — (Ϭ_B)_в = 2500 МПа, предел текучести алюминия примерно 30 МПа. Таким образом, для алюминия, армированного борными волокнами, получаем 1000 = 3250 V_B + 30(1 — V_B), а для углеалюминия — 1000 = 2500 V_B + 30(1 — V_B). Решение этих уравнений дает для бороалюминия V_B = 0,3 = 30 % (по объему), а для углеалюминия V_B = 0,39 = 39 % (по объему).

Из полученных результатов видно, что задача решается либо созданием бороалюминия, содержащего 39 % (по объему), либо — углеалюминия, армированного 46% (по объему) углеродных волокон.

Композиты такого состава будут иметь требуемую жесткость, прочность их будет выше заданной (это не очень выгодно с экономической точки зрения, но делать материалы менее прочными мы не имеем права, поскольку при уменьшении прочности за счет уменьшения концентрации волокон снижается и модуль Юнга).

Плотность полученных композитов также можно рассчитать по правилу смесей: ɣ = ɣ_B V_B + ɣ_М (1 — ɣ_B). Здесь ɣ, ɣ_B, ɣ_М — плотности композита, волокон и матрицы; V_B — объемная доля волокон.

Взяв значения плотностей борных и углеродных волокон (2630 кг/м 3 и 1700 кг/м 3 ) и зная, что ɣ_М = 2700 кг/м 3 , легко подсчитать, что плотность композита алюминий — 39 % (по объему) борных волокон составляет 2670 кг/м 3 , а композита алюминий — 46 % (по объему) углеродных волокон — 2240 кг/м 3 . Следовательно, требование по плотности выполнено тоже.

Дальше следует решить, на каком из двух выбранных композитов остановиться. Это определяется целым комплексом условий — технологических, конструкционных, экономических. В одних случаях более предпочтительным может оказаться бороалюминий, в других — углеалюминий.

Поскольку дополнительная информация не оговаривается, на этом можно остановиться, считая задачу, о том как создаются композиты, выполненной.