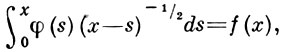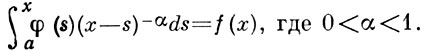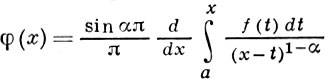Расстановка ударений: А`БЕЛЯ ИНТЕГРА`ЛЬНОЕ УРАВНЕ`НИЕ
АБЕЛЯ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — интегральное ур-ние
Видео:Интегральные уравнения с вырожденным ядромСкачать
где f(х) — известная ф-ция, φ(х) — искомая ф-ция. Получено и решено Н. Абелем (N. Abel) в 1823 при рассмотрении движения материальной точки в вертик. плоскости под действием силы тяжести. А. и. у. часто возникает при решении т. н. обратных задач, напр. при определении потенц. энергии по периоду колебаний или при восстановлении рассеивающего поля по эффективному сечению в классич. механике. А. и. у. относится к классу Вольтерры уравнений 1-го рода, рассматривают также обобщённое А. и. у.
. Если f(х) — непрерывно дифференцируемая ф-ция, то это ур-ние имеет единств, непрерывное решение:
В классе обобщенных функций решение существует при любых α.
Лит.: Гельфанд И. М., Шилов Г. Е., Обобщенные функции и действия над ними, 2 изд., М., 1959; Михлин С. Г., Лекции по линейным интегральным уравнениям. М., 1959.
- Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова — Бома эффект — Длинные линии. 1988. 704 с., ил.
ТЕМА 6. Неоднородное уравнение Фредгольма 2-го рода. Уравнения Фредгольма с вырожденными ядрами. Теоремы Фредгольма.
Видео:Интегральные уравнения Фредгольма второго рода Случай вырожденного ядра Неоднородный случайСкачать
- Алевтина Вышеславцева 5 лет назад Просмотров:
1 ТЕМА 6 Неоднородное уравнение Фредгольма -го рода Уравнения Фредгольма с вырожденными ядрами Теоремы Фредгольма Основные определения и теоремы Рассмотрим неоднородное уравнение Фредгольма yx ( ) = λ Kxs ( ) ysds ( ) + f( x) Сопряженным (союзным) интегральным уравнением называется уравнение с ядром K ( x = K( s x) Если ядро симметрическое то союзное уравнение совпадает с исходным Наряду с уравнением y( x) = λ K( x y( ds + f ( x) y = λ Ay + f будем рассматривать союзное с ним интегральное уравнение ψ ( x) = λ K ( x ψ( ds+ g( x) (в операторной форме ψ = λ A ψ + g ) g(x) — непрерывная функция Сформулируем 4 теоремы Фредгольма Теорема Однородное уравнение () ϕ( x) λ K( x ϕ( ds = и союзное с ним однородное уравнение () ψ ( x) λ K ( x ψ( ds= 4 или в операторной форме (K * (x =K(s x)) при любом фиксированном λ имеют либо только тривиальные решения либо одинаковое конечное число линейно независимых решений: ϕ ϕ ψ ψ В курсе лекций теорема была доказана для интегральных уравнений с вырожденными и симметрическими ядрами Теорема Для разрешимости неоднородного уравнения () ϕ( x) λ K( x ϕ( ds = f ( x) необходимо и достаточно чтобы f (x) была ортогональна всем линейно независимым решениям однородного союзного уравнения () ( f ( x) ψ ψ ψ если λ — характеристическое число) В курсе лекций теорема была доказана для случаев симметрических и вырожденных ядер Теорема (альтернатива Фредгольма) Либо неоднородное уравнение () разрешимо при любой неоднородности — непрерывной функции f (x) либо однородное уравнение () имеет нетривиальное решение В курсе лекций теорема была доказана для случаев симметрических и вырожденных ядер Теорема 4 Множество характеристических чисел однородного уравнения () не более чем счетно с единственной возможной предельной точкой
2 Этот результат справедлив для любого вполне непрерывного оператора В курсе лекций он был получен для вполне непрерывных самосопряженных операторов и тем самым доказан для случая симметрических ядер Для интегральных операторов с вырожденными ядрами результат тривиален Замечание В курсе лекций теоремы Фредгольма были доказаны для уравнений с симметрическими непрерывными ядрами и уравнений с непрерывными вырожденными ядрами Они справедливы и для общего случая произвольного непрерывного ядра так как имеет место следующая Теорема Интегральное уравнение Фредгольма рода y = λ Ay + f с невырожденным ядром при фиксированном λ можно заменить эквивалентным интегральным уравнением с вырожденным ядром Опишем процедуру решения неоднородного интегрального уравнения Фредгольма y( x) = λ K( x y( ds + f ( x) λay + f в случаях вырожденного ядра и симметричного ядра Напомним что ядро K ( x интегрального оператора Фредгольма называется вырожденным если оно представимо в виде K( x = ( x) ( где функции ( x) ( = непрерывны по своим аргументам на [ ] Не ограничивая общности можно считать что ( x) ( x) линейно независимы и ( ( также линейно независимы Рассмотрим уравнения Фредгольма рода yx ( ) = λ Kxs ( ) ysds ( ) + f( x) с вырожденным ядром функция K( x = ( x) ( где f (x) заданная непрерывная = Обозначив c = () s y() s ds будем иметь y( x) = λ c ( x) + f ( x) Для нахождения c получим эквивалентную систему алгебраических уравнений c = y( x) ( x) dx= λ c ( x) ( x) dx+ f( x) ( x) dx или i i i i = ki fi Обозначим определитель этой системы D( λ) = = c λ k c = f i= i i i = λk λk λk λk λk λk λk λk λk Теорема Если λ не является характеристическим числом (те D ( λ) ) то интегральное уравнение Фредгольма рода имеет решение при любой непрерывной неоднородности f (x) причем это решение единственно для каждой функции f (x) Решение алгебраической системы для c в этом случае может быть найдено например по формулам Крамера: c = D ( λ) f где D ( λ) — алгебраические i ki k D( λ ) k = ki 44
3 дополнения i-го столбца определителя D( λ ) ( D (λ) и D ( λ ) называются определителями Фредгольма) Подставляя или c в формулу y( x) = λ c ( x) + f ( x) получим yx ( ) f( x) λ D( λ) ( x) f( s ) ( sds ) = = + y ( x) = f ( x) + λ R( x s λ) f ( ds где резольвента интегрального оператора ki i k i= D( λ) k= ki R( xs λ) = Dki ( λ) i ( x) k ( D( ) λ i= k= Теперь рассмотрим интегральное уравнение Фредгольма -го рода в случае симметрического ядра Пусть ядро K ( x непрерывно по совокупности переменных симметрическое и K( x / λ — вещественное число f (x) — заданная непрерывная функция Пусть λ λ λ — последовательность характеристических чисел интегрального оператора которым соответствует ортонормированная система собственных функций ϕ ϕ ϕ (каждое характеристическое число повторяется в этой последовательности столько раз какова его кратность. ) Возможны два случая: а) λ k = Тогда решение можно записать в следующем виде λ k + λ y( x) = f ( x) f k ϕ k ( x) где fk = f() s ϕk() s ds k = λk λ — коэффициенты Фурье функции f ( x ) по ортонормированной системе собственных функций ϕ ϕ ϕ или ϕk( x) ϕk( y( x) = f( x) + λ f( ds= f( x) + λ R( x s λ) f( ds k = λk λ где k = R( x s λ ) ϕk( x) ϕk( Rxs ( λ) = — резольвента интегрального оператора Фредгольма λ λ k б) λ = λko где λ ko — характеристическое число интегрального оператора имеющее кратность r те ему отвечают r ортонормированных собственных функций ϕko( x) ϕ ko + r ( x) В этом случае решение не единственно и определяется формулой λ fk yx ( ) = f( x) + ϕk( x) + ckoϕko( x) + + cko+ r ϕko+ r ( x) λ λ k = k ko k k + r k где c ko c ko+ r — произвольные константы причем решение существует при условии ортогональности f (x) всем собственным функциям ϕko( x) ϕ ko + r ( x) соответствующим характеристическому числу λ ko Бесконечный ряд записанный в данном выражении сходится абсолютно и равномерно Заметим что решения отличаются одно от другого на функции являющиеся элементами Ker ( I λ A) (нуль-пространства) оператора I λ A Теорема А) Если однородное уравнение Фредгольма -го рода с непрерывным симметрическим ядром имеет только тривиальное решение (те λ k = ) то λ k 45
Видео:Интегральное уравнение АбеляСкачать
4 неоднородное уравнение имеет единственное решение для любой непрерывной функции f (x) Б) Если же однородное уравнение имеет нетривиальные решения (те λ = λk совпадает с одним из характеристических чисел) то неоднородное уравнение разрешимо в том и только том случае когда неоднородность непрерывная функция f (x) ортогональна всем собственным функциям соответствующим данному λ (ортогональна всем решениям однородного уравнения) В) В последнем случае если решение есть то оно не единственно Теорема (Альтернатива Фредгольма для интегральных уравнений Фредгольма -го рода с симметрическими ядрами): Либо неоднородное уравнение имеет решение при любой непрерывной функции f (x) либо однородное уравнение имеет нетривиальное решение Примеры решения задач Пример 6 Показать что характеристические числа однородного уравнения Фредгольма yx ( ) = λ ( s + sxysds ) ( ) и соответствующего однородного союзного уравнения ( ) = λ ( + ) ( ) zx x sxzsds совпадают и при этих λ указанные уравнения имеют одинаковое число линейно независимых решений Решение Обозначим sysds () = sy () s ds = zsds () = sz() s ds= Тогда решения указанных уравнений примут вид yx ( ) = λ+ λx zx ( ) = λx + λx и для определения коэффициентов получим λ λ = λ s ( + ds= = λ ( ) s + s ds= λ λ = λ ( s + ds= = λ s( s ds + = Итак при λ имеем = = y( x) z( x) = = при λ = остаются произвольными Поэтому λ = является характеристическим числом для обоих рассматриваемые уравнений и при этом λ они имеют по два линейно независимых решения: y( x) = y( x) = x и z( x) = x z( x) = x 46
5 Пример 6 Для каждого λ исследовать разрешимость и построить решение неоднородного уравнения Фредгольма -го рода с вырожденным несимметрическим ядром yx ( ) = λ ( s sxysds ) ( ) + x ( ) = λ ( ) ( ) sysds () = sy () s ds = тогда решение его имеет вид ( ) λ λ λ λ = λ s ( ds= = λ ( ) s s ds= Итак при Решение Рассмотрим соответствующее однородное уравнение Обозначим где yx s sxysds yx = x λ ± = = однородное уравнение имеет только тривиальное решение а значит исходное неоднородное уравнение имеет единственное решение При λ =± (характеристические числа) однородное уравнение имеет нетривиальные решения: если λ =+ то y ( x) = C если λ = то y ( x) Cx = Поэтому для указанных значений λ вопрос о разрешимости неоднородного уравнения сводится к проверке ортогональности функции f ( x) = x собственным функциям однородного союзного ( ) = λ ( ) ( ) уравнения zx x sxzsds Найдем собственные функции однородного союзного уравнения zsds () = sz() s ds= λ = λ ( s ds= При тогда решение его имеет вид λ = λ ( ) = s s s ds λ =+ получаем = — произвольно откуда f( x) z( x) dx= C x x dx= Обозначим zx ( ) = λx λx где z( x) Cx и те исследуемое уравнение разрешимо и решение его не единственно при λ = имеем = — произвольно откуда z ( x) Cx и f( x) z( x) dx= C x xdx те у исследуемого неоднородного уравнения решений нет Чтобы решить уравнения sysds () = sy() s ds= λ где = s ( λ λs+ s ) ds= снова обозначим yx ( ) = λ ( s sxysds ) ( ) + x тогда решение представимо в виде λ ( λ λ ) = s s+ s ds= + 5 yx ( ) x x = λ λ + 47
6 При λ = имеем = = следовательно решений нет как и было 5 установлено ранее при λ =+ получим = = C — произвольная постоянная поэтому 5 yx ( ) C x+ x те решение не единственно и определяется с точностью до собственной функции ядра y ( x) = C отвечающей λ = + 6 Если λ ± то = = и единственное решение дается формулой 5( + λ) 6λ x yx ( ) = + x 5( + λ) Пример 6 Построить резольвенту уравнения Фредгольма yx ( ) = λ si( x+ ysds ( ) + f( x) а) вычислив определители Фредгольма б) в виде разложения по собственным функциям однородного уравнения Решение а) Ядро исследуемого оператора K( x = si( x+ = si xcos s+ cos xsi s является вырожденным Обозначим ( six () cos () si элементы определителей Фредгольма k = ( x) ( x) dx: i i k = ( x) ( x) dx= sixcosxdx= k = ( x) ( x) dx= cosxcosxdx= k = ( x) ( x) dx= sixsixdx= k = ( ) ( ) cos si x x dx= x xdx= Вычислим определители Фредгольма: D( λ) = D( λ) = D( λ) = λ D( λ) = λk λk λk λ λk λk λk D( λ) = = = λ λ λk λk λk Искомая резольвента Rxs ( λ) = Dki ( λ) i ( x) k ( в случае D ( λ) D( λ ) i= k= те λ ± примет вид Rxs ( λ) = Dki ( λ) i ( x) k ( = D( λ ) i= k= si xcos s+ λ si xsi s+ λ cos xcos s+ cos xsi s si( x+ + λ cos( x = = λ λ 48
7 б) Характеристические числа и собственные функции однородного уравнения yx ( ) = λ si( x+ ysds ( ) были получены в примере 8: λ = и нормированная собственная функция y( x) = (six+ cos x) λ = и нормированная собственная функция y( x) = (six cos x) Подставляя их в формулу для резольвенты в случае ϕk( x) ϕk( симметрического непрерывного ядра Rxs ( λ) = имеем λ λ si( x + + λ cos( x (si x+ cos x)(si s+ cos (si x cos x)(si s cos Rxs ( λ) = + = λ λ λ Заметим что этот же результат был получен ранее методом последовательных приближений для «малого» λ (см пример 47) k = k yx ( ) = si xsi s+ s ysds ( ) + si x Пример 64 Решить уравнение ( ) Решение Обозначим si sy ( s ) ds = C sy() s ds = C тогда решение примет вид yx ( ) = ( Csi x+ C) + si x Постоянные C C могут быть найдены из системы C C C = si s ( si s+ + si ds= C C C C = s ( sis+ + si ds= C Итак C = C — остается произвольным C = C и искомое решение C определяется неоднозначно: yx ( ) = si x + (si x+ ) Замечание В рассматриваемом случае λ = совпадает с характеристическим числом однородного уравнения = λ ( + ) yx ( ) sixsi s s ysds ( ) Поэтому решение неоднородного уравнения оказалось не единственно и определилось с точностью до собственной функции соответствующего однородного уравнения отвечающей характеристическому числу λ = Действительно используя введенные выше обозначения решение однородного уравнения представим в виде yx ( ) = λ( Csi x+ C) Постоянные C C найдем из системы 49
Видео:Интегральные уравнения ВольтерраСкачать
8 C = si s λ( C si s+ C ) ds= λc C = s λ( Csi s+ C) ds= λc C( λ ) = Cλ C = нетривиальное решение которой C = C C = C существует при λ = Таким образом λ = — характеристическое число а ( ) (si ) y x = C x+ — отвечающие ему собственные функции Рекомендуем самостоятельно найти собственные функции однородного союзного уравнения zx ( ) = ( sixsi s x) zsds ( ) + и убедиться в выполнении условия разрешимости те ортогональности неоднородности f ( x) = six всем собственным функциям однородного союзного уравнения отвечающим характеристическому числу λ = Пример 65 Решение Решить уравнение Обозначим yx ( ) = xsysds ( ) + x C = sy() s ds тогда решение если оно существует можно записать в виде yx ( ) = C x+ x Подставляя это выражение в предыдущую формулу для определения постоянной C получим уравнение C = s ( C s + ds = C+ которое 5 решений не имеет Поэтому исследуемое интегральное уравнение Фредгольма yx ( ) = xsysds ( ) + xрешений также не имеет Замечание Элементарно устанавливается что λ = является характеристическим числом однородного уравнения Фредгольма yx ( ) = λ xsysds ( ) с собственной функцией y ( x) = C x Так как ядро симметрическое то λ = является также характеристическим числом однородного союзного уравнения с той же собственной функцией z ( x) = C x В рассматриваемом случае имеем λ = = λ те λ совпадает с характеристическим числом однородного уравнения При этом условие разрешимости (ортогональность неоднородности f ( x) = x всем собственным функциям однородного союзного уравнения) не выполнено 5
9 Пример 66 Рассмотрим неоднородное уравнение Фредгольма yx ( ) = λ Kxs ( ) ysds ( ) + f( x) с симметрическим непрерывным (невырожденным) ядром x ( x s K( x = s( x) s x xs [ ] ) При λ λ где λ = ( ) — собственные значения исследуемого интегрального оператора Фредгольма (см пример 77) построить резольвенту интегрального оператора и записать решение неоднородного уравнения ) Исследовать разрешимость уравнения при различных значениях λ и найти решение если оно существует в следующих случаях: а) f ( x) = si x б) f ( x) = x Решение ) Если λ λ = ( ) то используя построенную в примере 77 ортонормированную систему ϕ ( x ) = si x запишем соответствующую формулу для резольвенты интегрального оператора Фредгольма с симметрическим ядром ϕ( x) ϕ( six sis Rxs ( λ) = = = λ λ = λ Тогда решение неоднородного уравнения примет вид six sis y( x) = f( x) + λr( x s λ) f( ds= f( x) + λ f( ds = λ Меняя порядок суммирования и интегрирования в последней формуле получим решение в виде разложения в ряд по собственным функциям интегрального оператора Фредгольма с симметрическим ядром six f six y( x) = f ( x) + λ si s f ( ds = f ( x) + λ λ λ где f = = = si s f ( ds — коэффициенты Фурье по соответствующей ортонормированной системе ϕ ( x ) = si x ) Если λ λ = ( ) то неоднородное уравнение разрешимо при любой непрерывной функции f ( x ) Используя полученные выше формулы и вычисляя соответствующие интегралы имеем: si x sis si x 4 si x а) yx ( ) = si x+ λ si sds= si x+ λ = λ 4 λ 4 λ б) = + si x si s ( ) si x yx ( ) x = + λ sds= x+ λ = λ = ( λ) Если же такое что λ = λ = те λ совпадает с одним из характеристических чисел то ответ на вопрос о разрешимости уравнения зависит от конкретного вида функции f ( x ) В случае б) решение не существует ни при каких λ = λ = ( ) так как f ( x) = x при любом не ортогональна соответствующей собственной функции 5
10 ϕ ( x ) = si x однородного союзного уравнения (ядро симметрично поэтому однородное союзное уравнение совпадает с исследуемым при f( x) ) В случае а) необходимо рассмотреть два варианта При λ = 4 решение не существует так как неоднородность f ( x) = si x не ортогональна собственной функции ϕ( x) = si x однородного союзного уравнения отвечающей заданному значению λ = λ = 4 При λ = λ = 4 функция f ( x) = si x ортогональна собственной функции ϕ ( x ) = si x ( ) однородного союзного уравнения отвечающей рассматриваемому λ = λ = те решение существует но не единственно и sikx siks представимо в виде yx ( ) = si x+ sisds+ Csix где λ k= k k C — произвольная постоянная Меняя порядок суммирования и интегрирования заметим что все слагаемые в сумме при k равны нулю тк λ siks si s dx = ( k ) Поэтому учитывая что sis si sds = ( k = ) окончательно получим 4si x yx ( ) = si x + si x Csix Csix 4 + = 4 + где C — произвольно Задачи для самостоятельного решения 6 Построить резольвенту уравнений Фредгольма -го рода с симметрическим вырожденным ядром при значениях λ не совпадающих ни с одним их характеристических чисел: — через определители Фредгольма — в виде разложения по собственным функциям ядра: а) б) в) yx ( ) = λ xsysds ( ) + f( x) yx ( ) = λ ( x+ ysds ( ) + f( x) yx ( ) = λ ysds ( ) + f( x) г) yx ( ) = λ (+ cos( x ) ysds ( ) + f( x) д) yx ( ) = λ (si xsi s+ si xsi sysds ) ( ) + f( x) 6 Исследовать разрешимость при различных значениях λ и решить интегральные уравнения Фредгольма -го рода: а) yx ( ) = λ x( + ysds ( ) + x 5
11 б) в) г) д) е) ж) з) и) к ) л) yx ( ) = λ xysds ( ) + si x yx ( ) = λ (+ xsysds ) ( ) + x yx ( ) = λ xsi sysds ( ) + x s ysds x yx ( ) = λ rccos ( ) + 4 yx ( ) = λ tgs ysds ( ) + ctgx 4 yx ( ) = λ sixcos sysds ( ) + cosx yx ( ) = λ cos( x+ ysds ( ) + yx ( ) = λ ( + x ysds ( ) + si x ( ) = cos ( ) ( ) + si ( ) = λ ( + 5 ) ( ) yx λ x s ysds x yx xs xs ysds x м) yx ( ) = λ Kxs ( ) ysds ( ) + cos x где ( x + ) s x s K( x = ( s + ) x s x Ответы к задачам 6 а) б) в) г) д) xs xs Rxsλ ( ) = = λ λ λ(+ x + ( x+ Rxs ( λ) = 4λ Rxsλ ( ) = λ cos( x Rxsλ ( ) = + λ λ si xsi s+ si xsi s Rxsλ ( ) = λ 6 а) При 6 λ — единственное решение 5 x 7λ 6 yx ( ) = x + при λ = — решений нет 6 5λ 5 5
Видео:Метод определителей ФредгольмаСкачать
12 б) При λ — единственное решение yx ( ) = si x при λ = — yx ( ) = Cx+ si x- решение не единственно 6 в) При λ — единственное решение yx ( ) = x 7 6 при λ = — yx ( ) = x+ C(+ x) — решение не единственно 7 г) При λ — единственное решение x yx ( ) λ при λ = — решений нет д) При λ — единственное решение yx ( ) = λ + при λ = — решений нет x 8( λ) е) При всех λ — единственное решение λ yx ( ) = ctgx+ ж) При всех λ — единственное решение λ yx ( ) = cosx+ six 4λ six з) При λ ± — единственное решение yx ( ) = при λ = — решений нет + λ при λ = — yx ( ) = Ccosx six+ — решение не единственно λ и) При λ λ — единственное решение yx ( ) = si x+ x λ при λ = — решений нет x при λ = — yx ( ) = C+ si x+ — решение не единственно к) При λ λ six yx ( ) = λ при λ = — решений нет при λ = — yx ( ) = six+ C — решение не единственно 5 4 л) При λ λ — единственное решение ( ) 7 4 = + λ λ + x при λ = — решений нет при λ = — yx ( ) = + Cx x + 7x — решение не единственно 4 м) При λ λ ( ) — единственное решение x + e e (six+ cos x) yx ( ) = cosx+ λ + λ ( λ+ ) при λ = λ = — решений нет при λ = ( = 4) — решение не единственно x + e e (six+ cos x) yx ( ) = cos x+ λ C(six cos x) λ ( λ+ ) 54
🔍 Видео
Интегральные уравнения Фредгольма второго рода Случай вырожденного ядря Однородный случайСкачать
Простейшие интегральные уравненияСкачать
Интегральные уравнения Вольтерра второго рода Метод последовательных приближенийСкачать
Уравнения Фредгольма - 2Скачать
Метод решения интегрального уравнения Вольтерра второго рода с помощью резольвентыСкачать
Интегральное уравнение Вольтерра второго рода Пример решения методом разрешающего ядраСкачать
Решить интегральное уравнениеСкачать
Уравнения Фредгольма - 1Скачать
Уравнения Лагранжа второго рода. Задача 1Скачать
Альтернатива ФредгольмаСкачать
Ягола А. Г. - Интегральные уравнения - Уравнение Фредгольма 2-го рода с непрерывными ядрамиСкачать
Ягола А. Г. - Интегральные уравнения - Неоднородное уравнение Фредгольма 2-го родаСкачать
Интегральные уравнения Вольтерра второго рода Операционный метод для случаев разностного ядраСкачать
