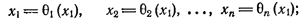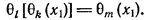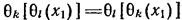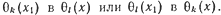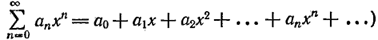Уравнение 5 степени в радикалах (4 видео)

Уравнение 5 степени в радикалах

Уравнение пятой степени в радикалах. Теорема Руффини — Абеля

Вернувшись из Копенгагена, Абель снова занялся алгебраическими уравнениями. Анализируя свое решение уравнения пятой степени, он понял, что ложным было не только это решение, но и сам подход к задаче. Вот что написал он об этом позже:

«Одной из интереснейших проблем алгебры является алгебраическое решение уравнений. Почти все выдающиеся математики исследовали этот вопрос. Без труда были получены общие выражения для корней уравнений первых четырех степеней. Для решения этих уравнений был открыт единый способ и надеялись, что он применим к уравнениям любой степени; но, несмотря на все усилия Лагранжа и других выдающихся математиков, поставленная цель не была достигнута. Предполагали решать уравнения, не зная, возможно ли это решение. В случае существования решения могли его получить, ничего о нем предварительно не зная; но если, к несчастью, решение не существовало, то его могли бы тщетно искать целую вечность. Для того чтобы получить наверняка некоторые результаты по этому вопросу, надо было выбрать иную дорогу, придав проблеме такой вид, чтобы она была всегда разрешима, а это можно сделать с любой проблемой. Вместо того, чтобы искать некоторое соотношение, не зная, существует оно или нет, надо спросить, возможно ли такое соотношение. Этот метод, который, без сомнения, является единственно научным, поскольку лишь он позволяет быть заранее уверенным в достижении поставленной цели, мало применяется в математике только потому, что его применение связано с исключительными трудностями. ».

Абелю удалось преодолеть эти трудности: он доказал, что общее уравнение пятой степени неразрешимо в радикалах — решения такого уравнения нельзя выразить через его коэффициенты с помощью арифметических действий и извлечения корней.

Таким образом, проблема, над которой математики бились веками, к началу 1824 года была полностью решена. Чтобы скорее сделать полученный результат достоянием математиков, Абель отпечатал брошюру с доказательством на французском языке за свой счет; из-за отсутствия средств ему пришлось сократить изложение до шести страниц и предоставить читателю додумать детали многих рассуждении. Неудивительно, что лишь немногие математики смогли полностью разобраться в содержании этой работы. Даже Гаусс, больше всех интересовавшийся теорией алгебраических уравнений, затерял брошюру Абеля среди своих бумаг. Впоследствии Абель опубликовал развернутое доказательство своей теоремы, занявшее несколько десятков страниц.

Вскоре выяснилось, что за несколько лет до Абеля аналогичный результат получил и итальянский ученый Паоло Руффини. И хотя доказательство Руффини было неполным, все же теорему о неразрешимости уравнения пятой степени в радикалах теперь называют теоремой Руффини — Абеля.

Но хотя общее уравнение пятой степени и нельзя решить в радикалах, существует целый ряд частных случаев, в которых такое решение возможно. Например, разделить угол a на n равных частей значит выразить cos a через cos (a/n) и решить получившееся уравнение относительно cos (a/n). Так как

cos a = 4 cos 3 (a/3) — 3 cos(a/3)

то при n = 3 получаем кубическое уравнение которое, как и всякое кубическое уравнение, решается в радикалах. Оказывается, такие уравнения решаются в радикалах при любых значениях n. Аналогичные уравнения получаются и при переходе от тригонометрических функций к эллиптическим. Абелю удалось написать эти уравнения, выразив эллиптические функции аргумента х через функции аргумента х/n.

Абель знал, что вопрос о разрешимости уравнения в радикалах связан с соотношениями между корнями уравнения. Например, все корни уравнения

x n-1 + x n-2 + . + x + 1= 0, (2)

возникающего при деление круга на n частей (поэтому уравнение (2) называется уравнением деления круга), можно выразить через один из них следующим образом:

Функции y = x, y = x 2 . y = x n-1 рациональны. При этом они обладают следующим замечательным свойством: если взять любые две такие функции, заменить в одной из них х другой функцией и вместо х подставить x₁, то полученное число снова будет одним из корней уравнения. В самом деле, из уравнения (2) следует, что x₁ n = 1, а потому (x₁ k ) l = x₁ kl = x₁ m где m — остаток от деления kl на n.

Абель понял, что именно с этим свойством связана разрешимость в радикалах уравнения деления круга. Поэтому он рассмотрел такие уравнения, что:

а) все корни каждого из них могут быть представлены в виде рациональных функций от одного из корней, например, от x₁:

б) функции 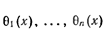таковы, что для любых k и l найдется такое m, что

Оказалось, что для разрешимости уравнения в радикалах достаточно выполнения еще одного условия: для любых k и l

Иными словами, нужно, чтобы не имело значения, подставим ли мы

С тех пор совокупности преобразований, результат последовательного выполнения которых не зависит от порядка вы-полняемых преобразований, называют абелевыми (или коммутативными).

При изучении эллиптических функций и интегралов Абель широко использовал теорию степенных рядов. Степенным рядом называется выражение вида

Он доказал, что множество значений х, для которых сходится ряд

является или промежутком вида ]—l, l[ (где l может также равняться нулю или бесконечности), или таким же промежутком, к которому присоединены один или оба конца. Он доказал, что на промежутке сходимости степенной ряд можно почленно дифференцировать и интегрировать и исследовал поведение суммы ряда при приближении х к концам промежутка сходимости. Все эти результаты сразу после их опубликования стали классическими и вошли во все курсы высшей математики.

Описанный круг идей Абель разрабатывал на протяжении 1824—1826 годов, когда, окончив университет, отправился за границу для продолжения образования. Он побывал в Германии, Австрии, Италии, Швейцарии, Франции, Бельгии, познакомился с Якобом Штейнером, Андриеном Лежандром, Огюстеном Коши и многими другими математиками.

По материалам книги
«Замечательные ученые»
под ред. С.П. Капицы

Содержание

О теореме Абеля-Руффини без групп и теории Галуа
Историческая справка
Мотивация данной статьи
Решения уравнений в радикалах
Неразрешимость уравнения 5-й степени
Заключение
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Решение уравнений в радикалах
Уравнение третьей степени: формула Кардано
Анализ формулы Кардано для полиномов с вещественными коэффициентами
Уравнение четвертой степени
Преобразование Чирнгауза
Разрешимость в радикалах
Задачи
Источники
🔍 Видео

Видео:Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

О теореме Абеля-Руффини без групп и теории Галуа

Историческая справка

Поиск решения алгебраических уравнений оказал колоссальное влияние на развитие математики. Формула решения общего кубического уравнения впервые была получена итальянскими математиками 16-го века. Это событие ставшее первопричиной рассмотрения комплексных чисел, считается одним из поворотных моментов в истории математики. Судьбы Джероламо Кардано, Никколо Тартальи, Сципиона дель Ферро и их поисков решения кубического уравнения заслуживают отдельного романа со своими интригами, скандалами и расследованиями. Столь яркие истории достаточно редки в математике.

Начиная с 19-го века поиск формул для решения уравнений произвольных степеней положил начало теории групп и абстрактной алгебре, которые преобразили практически все разделы современной математики. Думаю, многие, кто интересовался историей и развитием алгебры, знают, что формулы для решения общего алгебраического уравнения степени выше четвертой не существует. Как сообщается, первое доказательство этого факта было дано итальянским математиком Паоло Руффини в самом конце восемнадцатого века, оно составляло около 500 страниц и все же содержало некоторые пробелы. Хотя отдельные математики, как Огюстен Коши, и признавали данное доказательство, но ввиду столь большого объема и сложности изложения, оно так и не было принято математическим сообществом. Считается, что первое полное доказательство дано норвежским математиком Нильсом Абелем и содержалось в двух работах, изданных в 1824 и 1826 годах. С тех пор оно носит название теоремы Абеля или теоремы Абеля-Руффини.

Если вы попытаетесь изучить это доказательство в его современном изложении, то окажется, что оно практически полность опирается на Теорию Галуа. Эварист Галуа был французским математиком 19-го века и современником Нильса Абеля. Помимо занятий математикой он вел активную политическую жизнь из-за чего несколько раз попадал в тюрьму. В возрасте всего двадцати лет был застрелен на дуэли, поводом для которой послужила любовная интрига, хотя есть предположения, что дуэль была подстроена его политическими противниками. Об этой истории написано достаточно много, кроме того, имеется перевод на русский язык его мемуаров и писем. Последнее письмо его другу Огюсту Шевалье было написано в ночь накануне дуэли, в нем он наспех излагает свои последние идеи. Несмотря на столь короткую жизнь, Эварист Галуа считается одним из родоначальников современной алгебры. Хотел бы заметить, что в популярном изложении создается некий романтический образ Галуа, как подростка-гения, который в одиночку, с нуля создал теорию групп и преобразил всю алгебру. Несомненно его идеи сыграли огромную роль, но если почитать его сочинения, то мы увидим, что он хорошо знал и опирался на знаменитые работы Лагранжа, Эйлера, Гаусса, Абеля, Якоби. Зачатки теории групп и перестановок появляются еще в работах Жозефа Луи Лагранжа по теории алгебраических уравнений, а также Карла Фридриха Гаусса в его знаменитых «Арифметических исследованиях». К тому же, теория Галуа в современном изложении была оформлена многими последующими математиками — Дедекиндом, Кронекером, Гильбертом, Артином и другими.

Мотивация данной статьи

Чуть менее года назад меня сильно увлекла статья об истории решения кубического уравнения и последующих безуспешных поисков формулы уравнения 5-й степени, длившихся почти триста лет. Сразу хочу отметить, что специального математического образования у меня нет и поэтому, попробовав прочесть современную версию доказательства теоремы Абеля-Руффини, я естественно ничего не понял. В моем сознании термины группа, кольцо и поле никак не ассоциировались с алгебраическими структурами. Но желание разобраться было столь велико, что я принялся за изучение курса высшей алгебры.

На первых этапах абстрактная алгебра была наверное самым сложным из того, что мне приходилось изучать ранее. Объем новых терминов и определений просто зашкаливал: группы, факторгруппы, моноиды, поля, кольца, тела, модули, идеалы, ядра, векторные пространства, биекции, сюръекции, инъекции, изоморфизмы, автоморфизмы, гомоморфизмы, эндоморфизмы и тд. Спустя несколько месяцев упорных занятий, я начал понимать формальную часть, но, к сожалению, интуитивного понимания, которое и являлось моей изначальной целью, я так и не достиг.

Дело в том, что практически все современные доказательства неразрешимости уравнений 5-й степени в радикалах сводятся к следующему. Рассматривается некоторое неприводимое уравнение, например x 5 -10x+2, после чего методами мат анализа определяется, что оно имеет три действительных и два комплексно-сопряженных корня. После чего заключается, что группой Галуа данного уравнения есть группа S₅, которая не является разрешимой, и следовательно данное уравнение неразрешимо в радикалах. Доказательство теоремы Абеля-Руффини о неразрешимости общего уравнения также сводится к неразрешимости группы S_n. Для меня данные доказательства были слишком абстрактными и оторванными от конкретных уравнений. Когда я пытался представить их в терминах элементарных алгебраических операций, чтобы понять в чем заключается главная причина неразрешимости уравнений, у меня ничего не получалось. Возможно для тех, кто занимается этим достаточно долго, эти вещи могут казаться интуитивно понятными.

Немного иной подход описан в книге Алексеева «Теорема Абеля в задачах и решениях», основанной на лекциях Владимира Арнольда, но в изложенном там доказательстве помимо теории групп используются элементы комплексного анализа и Римановых поверхностей. Я также находил похожие статьи, использующие топологические аргументы в виде комбинаций петель и коммутаторов, но мне хотелось найти что-то чисто алгебраическое.

Параллельно изучая историю математики и понимая, что современная формулировка и доказательство сильно отличаются от того, как излагали свои идеи Лагранж, Руффини, Абель и Галуа, я решил прочесть первоисточники. К сожалению, на русский или английский по этой теме переведены лишь сочинения Галуа и одна из работ Абеля.

После некоторых поисков я наткнулся на статью 1845 года французского математика Пьера Лорана Ванцеля, в которой он переработал и сильно упростил доказательство Абеля-Руффини, о чем он пишет во введении. В этой работе, он так же упоминает мемуары Галуа и отмечает, что они будут опубликованы в скором времени. Для заметки — работы Галуа были опубликованы лишь в 1846 году Жозефом Лиувиллем, спустя почти 15 лет после смерти Галуа. Кстати, Пьер Лоран Ванцель, также был первым, кто доказал неразрешимость трисекции угла и удвоения куба с помощью циркуля и линейки — знаменитых задач стоявших еще со времен античности. Доказательства Ванцеля были изложены без использования абстрактной алгебры и теории Галуа, поскольку на тот момент они еще не были разработаны. Хотя работа и была доступна лишь на французском, которого я до этого практически не знал, но ввиду специфической темы, небольшого размера (всего 7 страниц) и наличия гугл переводчика, я справился достаточно быстро. По моему субъективному мнению, его доказательство теоремы Абеля-Руффини является наиболее простым для понимания.

Уже позже я нашел пример подобного доказательства основанного на работе Руффини в книге Чеботарёва “Основы Теории Галуа”. Далее я постараюсь кратко изложить принцип решения уравнений в радикалах и идею доказательства неразрешимости уравнения 5-й степени.

Решения уравнений в радикалах

Для дальнейшего понимания, потребуются минимальные пререквизиты:

Формулы Виета — напомню, что коэффициенты произвольного уравнения являются элементарными симметрическими функциями от его корней, то есть функциями, которые не меняют своего значения при любых перестановках корней. Примеры: x₁ + x₂ + x₃, x₁x₂x₃, x₁x₂ + x₁x₃ + x₂x₃.

Теорема о симметрических многочленах — каждую симметрическую функцию от корней, можно выразить с помощью элементарных симметрических функций (коэффициентов уравнения).

Первообразные корни n-й степени из единицы — комплексные величины не равные единице, но n-я степень которых, равна единице. Примеры: (-1) 2 = 1, (-1/2 + sqrt(-3)/2) 3 = 1, i 4 = 1 соответственно квадратный, кубический и биквадратный корни из единицы.

Основная теорема алгебры — гласит о том, что уравнение n-й степени с комплексными коэффициентами имеет ровно n комплексных корней с учетом кратности (корни могут быть одинаковые).

Первоначальная идея восходит к работе Жозефа Луи Лагранжа “Размышления о решении уравнений” 1770-1771 годов. Это достаточно объемное сочинение и я не нашел его перевода на русский или английский язык. Как указывается в разных источниках, в попытке найти формулу для уравнения 5-й степени, Лагранж проанализировал все имеющиеся к тому времени способы решения уравнений и выделил общий принцип, позволяющий решить уравнения 4-й и низших степеней. В этой же работе, изучая перестановки корней, он пришел к теореме, которая сейчас носит его имя. Принцип, открытый Лагранжем, заключался в том, чтобы найти выражения от корней заданного уравнения n-й степени, которые при всех возможных перестановках этих корней принимали n-1 значений, но в тоже время через них выражались первоначальные корни. На эти значения, можно составить уравнение n-1 степени и повторить операцию, тем самым сводя изначальное уравнение к цепочке уравнений меньших степеней, решив которые, можно получить корни первоначального уравнения. Рассмотрим один из примеров:

Пусть f(x) = x 4 + ax 3 + bx 2 + cx + d общее уравнение 4-й степени с произвольными коэффициентами a, b, c, d и x₁, x₂, x₃, x₄ его корни.

Напомним, что его коэффициенты — это элементарные симметрические функции от корней, в чем можно убедиться просто раскрыв скобки в выражении (x — x₁)(x -x₂)(x — x₃)(x — x₄):

Так как корни являются произвольными, то существует 4! = 24 различных вариантов их расположения, но можно составить выражение x₁x₂ + x₃x₄, которое принимает всего три разных значения при всех 24-х перестановках корней:

На эти три значения мы можем составить уже кубическое уравнение, корнями которого они и будут являться. Таким образом, мы сводим решение уравнения 4-й степени к уравнению 3-й степени. Для решения кубического уравнения мы можем воспользоваться резольвентой Лагранжа (y₁ + wy₂ + w 2 y₃) 3 , где w — это кубический корень из единицы. Данное выражение принимает всего два разных значения при всех возможных 3! = 6 перестановках. Оно будет сохранять значение при циклических перестановках и менять знак при любой транспозиции. Получим:

Теперь составим квадратное уравнение на z₁ и z₂:

z₁+z₂ и z₁z₂ — будут симметрическими функциями от корней нашего изначального уравнения f(x), следовательно, по теореме о симметрических многочленах, напрямую выражаться через коэффициенты a, b, c, d. Решив квадратное уравнение мы получим значения z₁, z₂. После чего, извлекая кубические корни из z₁, z₂, и складывая с коэффициентом b, сможем выразить y₁. Далее, c помощью y₁ и коэффициентов a, b, d, решив два квадратных уравнения, мы доберемся до корней x₁, x₂, x₃, x₄ изначального уравнения.

Данный пример показывает, что произвольное уравнение 4-й степени решается путем составления вспомогательных кубического и квадратных уравнений. Далее я приведу рассуждение, почему подобный прием невозможен для общего уравнения 5-й степени.

Неразрешимость уравнения 5-й степени

Итак, мы хотим показать, что ни один корень общего уравнения 5-й степени не может быть выражен через его коэффициенты путем решения цепочки вспомогательных двучленных уравнений низших степеней.

Пусть f(x) = x 5 + ax 4 + bx 3 + cx 2 + xd + e общее уравнение 5-й степени с произвольными коэффициентами a, b, c, d, e и x₁, x₂, x₃, x₄, x₅ его корни. Обозначим за y₁ первый радикал входящий в значение x₁ в порядке вычисления. Пусть y₁ n = p, где p будет какой-то симметрической функцией от корней и, следовательно, напрямую выражаться через коэффициенты a, b, c, d, e. Заметим, что y₁ уже не будет симметрической, а лишь рациональной функцией g от корней — g(x₁, x₂, x₃, x₄, x₅). Следовательно, g должно менять значение при перестановке любых двух корней. Тогда эти значения будут являться корнями уравнения y₁ n = p, которые имеют вид g, zg, z 2 g, z 3 g … z n-1 g, где z — первообразный корень n-й степени из единицы (z n =1). Рассмотрим произвольную транспозицию, например (x₁, x₂), тогда

если мы применим ее еще раз, то получим:

Из этого следует, что z 2 = 1, то есть z должен быть квадратным корнем из единицы (z = -1) и соответственно первый радикал y₁ будет квадратным. Поясним: так как корни являются произвольными, то g должно сохранять значение при любых четных перестановках корней и менять знак при нечетных. Теперь покажем, что значение функции g не будет меняться при циклической перестановке трех корней (x₁, x₂, x₃). Здесь стоит пояснить, что циклическая перестановка (x₁, x₂, x₃) четная и может быть представлена, как произведение транспозиций (x₁, x₂)(x₂, x₃). То есть, функция g не поменяет своего значения при данной перестановке. Еще заметим, что функция g не изменится при циклической перестановке пяти корней, так как она так же раскладывается в произведение четного количества транспозиций. Присоединяя радикал y₁ к выражениям от коэффициентов с помощью базовых арифметических операций, мы будем получать симметрические функции относительно всех циклов на трех и пяти корнях и вообще любых четных перестановок, но при перестановке содержащей нечетное количество транспозиций, y₁ будет менять знак. Дальнейшее присоединение квадратных радикалов не даст нам ничего нового. Теперь предположим, что мы пришли к радикалу, который меняет свое значение лишь при тройных циклах. Обозначим его y₂, тогда y₂ n = q, где q — это рациональная функция от коэффициентов a, b, c, d, e и радикала y₁.

В данном случае z 3 = 1, то есть z здесь будет кубическим корнем из единицы.

Теперь произведем циклическую перестановку 5-и корней

Так как z должен быть кубическим корнем из единицы, как мы выяснили ранее, то единственным вариантом будет z = 1 и g должна быть инвариантна при любой из этих циклических перестановок. Но тогда она должна быть инвариантна и при циклической перестановке x₃,x₂,x₅,x₁,x₄ -> x₂,x₅,x₁,x₄,x₃. Отсюда, одной транспозицией мы можем получить, что

но, выше мы уже видели, что

а из этого следует

что приводит нас к противоречию, так как мы предполагали, что g меняет значение при циклической перестановке трех корней (x₁, x₂, x₃).

Еще одним вариантом, было бы показать что все четные перестановки на пяти корнях порождаются тройными циклами, то есть, если есть тройные циклы, то никаких выражений от корней, которые бы сохраняли набор значений при всех четных перестановках, не существует. Если теперь перевести это на теоретико-групповой язык, то получается, что группа общего уравнения пятой степени есть симметрическая группа S₅, в которой существует 5! = 120 различных перестановок пяти корней. Далее, путем присоединения квадратного корня из дискриминанта, мы можем понизить ее до знакопеременной группы четных перестановок A₅, которая содержит 120/2 = 60 перестановок. Но A₅ является простой группой, в которой нет никаких нетривиальных нормальных подгрупп, которым бы соответствовали выражения от корней сохраняющие значения при определенных перестановках, из чего следует, что присоединение любых дополнительных радикалов не приблизит нас к решению.

Заключение

Поводом для написания данной статьи послужило желание структурировать свои мысли по этой теме и представить идеи о неразрешимости уравнений в радикалах без привлечения абстрактной алгебры и теории Галуа. По моему мнению, в подавляющем большинстве современных изложений теряется связь между областью, в которой происходит доказательство и конкретными уравнениями. Если у кого-то есть замечания, дополнения или ссылки на подобные элементарные изложения, буду рад услышать.

Видео:Сможешь решить уравнение пятой степени?Скачать

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Вспомогательная страница к разделу ПОЛИНОМ

Видео:Начала теории Галуа: разрешимость алгебраических уравнений в радикалахСкачать

Решение уравнений в радикалах

Можно ли выразить корни полинома $ f(x)=a_x^n+a_1x^+dots+a_n $ с комплексными коэффициентами $ a_,a_1,dots,a_n $ в виде «хороших» функций от этих коэффициентов? Вспомним, что для корней квадратного уравнения существует общая формула вычисления корней: $$x^2+ax+b=0 Rightarrow lambda_=frac<-apm sqrt> . $$ Эта формула включает в себя элементарные алгебраические операции $ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии можно сформулировать и общую задачу.

Задача. Найти выражения корней полинома степени $ n > 2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических операций и операций извлечения корней произвольных (целых) степеней.

Поставленная задача называется задачей о разрешимости уравнения в радикалах 1) .

Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_(x)=0 $ делится на старший коэффициент полинома $ f_(x) $.

Полином называется нормализованным, если его старший коэффициент равен $ 1_ $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.

Очевидно, что нормализованный полином имеет те же корни (и в тех же кратностях ), что и исходный. Для простоты обозначений, будем считать, что полином уже нормализован: $$ f(x)=x^n+a_1x^+dots+a_n , .$$

Второе упрощение заключается в замене переменной (подстановке): $ x=y +alpha $. Ее результатом будет новый полином той же степени, что и исходный, относительно переменной $ y $: $ F(y)equiv f(y+alpha) $. Корни нового полинома связаны (cм. преобразование 2 ☞ ЗДЕСЬ ) с корнями старого по формуле $ lambda_j = Lambda_j+alpha $; так что, найдя корни одного полинома, легко установим и корни другого. Подберем теперь параметр $ alpha $ так, чтобы обратить в нуль коэффициент при $ y^ $ в полиноме $ F(y) $. Используя формулу бинома Ньютона, получаем $$ begin f(x)&=&x^n+a_1x^+a_2x^+dots+a_n= \ &=&(y+alpha)^n +a_1(y+alpha)^+a_2(y+alpha)^+dots+a_n = \ &=&y^n + C_n^1 alpha y^ +C_n^2 alpha^2 y^+dots+ alpha^n + \ & & qquad + a_1y^+a_1 C_^1 alpha y^+dots +a_1alpha^ + \ & & quad qquad qquad +a_2y^ + dots + a_n. end $$ Понятно, что если положить $ alpha= — a_1/n $, то коэффициент при $ y^ $ исчезнет. Для простоты обозначений будем считать, что полином уже предварительно подвергнут такому преобразованию: $ f(x)=x^n+a_2x^+dots+a_n $.

Видео:Уравнение четвертой степени Скачать

Уравнение третьей степени: формула Кардано

Рассмотрим уравнение третьей степени: $$ x^3+p,x+q=0 $$ Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные $ u_ $ и $ v_ $; получим: $$ u^3+v^3+3,uv(u+v)+p(u+v)+q=0 . $$ Сгруппируем: $$ u^3+v^3+(3,uv+p)(u+v)+q=0 . $$ Подчиним теперь неизвестные $ u_ $ и $ v_ $ условию $$ 3,uv+p=0 iff uv=-frac

. $$ Тогда предыдущее уравнение приведется к виду $$u^3+v^3=-q . $$ Итак, для определения неизвестных величин $ u_ $ и $ v_ $ мы получили систему уравнений $$ u^3+v^3=-q, uv=-frac

. $$ Возведя последнее уравнение в куб, получим $$ u^3v^3=-frac

. $$ Два полученных равенства, связывающие $ u^ $ и $ v^ $, позволяет утверждать, что эти величины являются решениями квадратного уравнения: $$t^2+q,t- frac

=0 .$$

Выражение $$ Delta = frac+frac

$$ называется дискриминантом кубического уравнения.

Решив квадратное уравнение, получим: $$ u^3=-frac+ sqrt, v^3=-frac— sqrt . $$ В итоге имеем формулу для решений уравнения: $$ x=u+v=sqrt[3]<-frac+sqrt<frac+frac

>>+ sqrt[3]<-frac-sqrt<frac+frac

>> ; $$ она называется формулой Кардано.

Исторические заметки об открытии метода решения кубического уравнения ☞ ЗДЕСЬ.

Формула Кардано не очень удобна для практических вычислений. Дело в том, что корень кубический из комплексного числа принимает три различных значения. Решение же, представленное формулой Кардано, имеет в правой части комбинацию из двух кубических корней. Таким образом, получаем 9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только три решения. Для того, чтобы установить соответствие между значениями $ u_ $ и $ v_ $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание значений для $ u_ $ позволит однозначно восстановить $ v_ $. Пусть $$ u_1=sqrt[3]<-frac+sqrt<frac+frac

>> $$ какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы (см. ☞ ЗДЕСЬ ): $$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$ при $$varepsilon_1=cos frac + sin frac= -frac+ frac<sqrt> u varepsilon_2=cos frac + sin frac= -frac- frac< sqrt> . $$ Если теперь взять $$ v_1=-frac

, $$ то решения кубического уравнения можно выразить в виде комбинаций $ u_1 $ и $ v_1 $: $$ begin lambda_1&=&u_1+v_1, \ lambda_2&=&u_2+v_2=u_2-frac=u_1varepsilon_1-frac =u_1varepsilon_1-frac=u_1varepsilon_1+v_1varepsilon_2,\ lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 . end $$ Окончательно получаем формулы для вычисления корней: $$ left< begin lambda_1&=&u_1+v_1, \ lambda_2&=&-frac(u_1+v_1) + frac<scriptstyle sqrt> (u_1-v_1),\ lambda_3&=&-frac(u_1+v_1) — frac<scriptstyle sqrt> (u_1-v_1), end right. $$ где $ u_ $ — одно из значений корня кубического, а $ v_ $ связано с ним соотношением $ v_1=-p/(3u_1) $.

Пример [1]. Решить уравнение $ x^3-6,x^2-10,x+8 =0 $.

Решение. Подстановка $ x=y+2 $ приводит уравнение к виду $$y^3+2,y+4 =0 , $$ т.е. $ p=2,,q=4 $. Далее $$Delta=-frac Rightarrow sqrt = pm frac<10 ><3sqrt> Rightarrow u_1=sqrt[3]<left(-2 + frac<3sqrt> right)> . $$ Одно из значений последнего корня: $$u_1=-, sqrt[3]<-2 + frac<3sqrt>> , $$ это выражение можно упростить, если повезет заметить, что подкоренное выражение равно $ left(-1+1/<sqrt>right)^3 $: $$u_1=left(1-frac<sqrt>right) Rightarrow v_1=-frac

= left(1+frac<sqrt>right) . $$ Получаем: $$mu_1=2, , mu_2=1- , mu_3=-1- .$$ Значения корней исходного уравнения получатся «сдвигом» на $ 2 $.

Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Анализ формулы Кардано для полиномов с вещественными коэффициентами

Пусть коэффициенты $ p^ $ и $ q^ $ уравнения $ x^+p,x+q=0 $ вещественны. Тогда и дискриминант $$ Delta = frac+frac

$$ этого уравнения — тоже вещественное число. В зависимости от знака этого числа, уравнение будет иметь разное число вещественных корней.

I. Пусть $ Delta>0 $. Тогда $ sqrt $ является числом вещественным, и мы будем считать его положительным. В формуле для $ u_1=sqrt[3]<-q/2+sqrt> $ в качестве значения кубического корня возьмем единственное его вещественное значение: $$ u_1 in mathbb R Rightarrow v_1 in mathbb R .$$

Согласно формулам $$ begin lambda_1&=&u_1+v_1, \ lambda_2&=&u_2+v_2=u_2-frac=u_1varepsilon_1-frac =u_1varepsilon_1-frac=u_1varepsilon_1+v_1varepsilon_2,\ lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 . end $$ получим: корень $ lambda_ $ уравнения веществен, а $ lambda_ $ и $ lambda_ $ — мнимы и комплексно-сопряжены.

Пример. Решить уравнение $$ x^3-frac , x-frac =0 . $$

Решение. Здесь $$p=-frac, q=-frac, Delta=frac, u_1=sqrt[3]<frac+frac<5 sqrt>> , v_1=sqrt[3]<frac-frac<5 sqrt>> . $$ Единственный вещественный корень должен получаться в виде суммы чисел $ u_ $ и $ v_ $ — «сильно» иррациональных, судя по внешнему виду. Тем не менее, этот корень очевиден: $ lambda = 1 $.

Объяснить эту кажущуюся несуразность можно если заметить, что выражения под кубическими корнями в $ u_ $ и $ v_ $ представимы в виде кубов: $$frac+frac<5 sqrt>=left(frac +frac<sqrt> right)^3 ,quad frac-frac<5 sqrt>=left(frac -frac<sqrt> right)^3 .$$ Тогда и два оставшихся корня $ -1/2 pm 1/2 , mathbf i $ получаются из общих формул. ♦

II. Пусть $ Delta=0 $. Формулы для корней дают $$ lambda_1=2 sqrt[3] , lambda_2= sqrt[3] , , lambda_3= sqrt[3] , $$ т.е. уравнение имеет кратный корень кратности $ 2_ $ если $ qne 0 $ и кратности $ 3_ $ если $ q=0 $.

III. Пусть $ Delta ♦

В только что рассмотренном примере формула Кардано позволяет получить вещественные корни полинома — даже если для их выражения приходится иметь дело с мнимыми числами. Попробуем, однако, применить тот же прием ко следующему примеру.

Пример [2]. Решить уравнение $ x^3-3,x+1=0 $.

Решение. Здесь $ Delta=-frac $ и $ u_1=sqrt[3]<-frac + frac<sqrt>, mathbf i> $. $$sqrt[3]<-frac + frac<sqrt>, mathbf i>= alpha+ mathbf i, beta Rightarrow 4, alpha^3-3, alpha +frac =0 . $$ Умножив последнее уравнение на $ 2_ $ и сделав в нем замену переменной $ A = 2alpha $ мы придем к уравнению $$A^3-3, A +1 =0 , $$ т.е. вернемся к исходному уравнению!

Вывод: все корни полинома вещественны, но в радикалах их можно представить только с помощью мнимых чисел. ♦

Как разрешить этот парадокс?

Как получить вещественный вид для корней полинома? На помощь приходит альтернативный алгебраическому способ извлечения корня кубического из комплексного числа: способ, основанный на представлении этого числа в тригонометрической форме.

Теорема. В случае $ Delta ♦

Пример. Решить уравнение из предыдущего примера: $ x^3-3,x+1=0 $.

Решение. Здесь $ p=-3, q=1 $ и $ displaystyle varphi = operatorname left(- frac right) =frac $.

Ответ. $$ 2 cos frac approx 1.53208 ,quad 2 cos frac approx -1.87938 , quad 2 cos frac approx 0.34729 . $$ Проверка может быть выполнена применением формулы приведения для степени косинуса, приведенной ☞ ЗДЕСЬ.

Пример. Решить уравнение $ x^3-6,x+3=0 $.

Решение. Здесь $ p=-6, q=3 $ и $ displaystyle varphi = operatorname left(- frac<4sqrt> right) approx 2.1297861 $.

Ответ. $ approx 2.145103, approx -2.669079, approx 0.523976 $.

Видео:Уравнение 5-ой степени ➜ Простой способ решенияСкачать

Уравнение четвертой степени

рассмотрим в виде: $$ x^4+p,x^2+q,x+r=0 , $$ перепишем его в виде $$x^4=-p,x^2-q,x-r $$ и прибавим к обеим частям $ x^2t+t^2/4 $, где $ t $ — новая неизвестная: $$ x^4+x^2t+t^2/4=(t-p),x^2-q,x +(t^2/4-r) . $$ Левая часть получившегося уравнения является полным квадратом: $$ left(x^2+t/2 right)^2 =(t-p),x^2-q,x+(t^2/4-r) . $$ Подберем теперь значение $ t $ так, чтобы и правая часть стала полным квадратом.

Теорема. Для того, чтобы квадратный полином $ Ay^2+By+C $ был квадратом полинома первой степени, необходимо и достаточно, чтобы его дискриминант $ B^2-4,AC $ был равен нулю.

Доказательство. Необходимость. Если $ Ay^2+By+Cequiv (ky+ ell)^2 $, то $ A=k^2,, B=2,kell,, C=ell^2 $ и тогда очевидно $ B^2-4,AC=0 $.

Применяя этот результат к правой части полученного уравнения, находим условие на параметр $ t $, при котором это выражение станет полным квадратом: $$ q^2-4,(t-p)(t^2/4-r)=0 iff t^3-p,t^2-4,r,t+(4,pr-q^2)=0 $$ Это уравнение называется резольвентой Феррари для уравнения $ x^4+p,x^2+q,x+r=0 $.

Поскольку резольвента Феррари является уравнением кубическим, то его можно разрешить в радикалах по методу изложенному ВЫШЕ. Обозначим через $ t_1 $ какой-то из его корней. При этом значении $ t $ правая часть уравнения $$ left(x^2+t/2 right)^2 =(t-p),x^2-q,x+(t^2/4-r) . $$ будет полным квадратом: $$ (t_1-p),x^2-q,x+(t_1^2/4-r) equiv left(Kx+L right)^2 quad npu quad K= sqrt,, L= -frac<2sqrt> . $$ Следовательно, уравнение это уравнение приобретает вид: $$ left(x^2+ t_1/2 right)^2 = left(Kx+L right)^2 $$ и разлагается на два квадратных: $$ x^2+t_1/2 =Kx+L quad u quad x^2+t_1/2 =-Kx-L . $$ Последние, по их решении, и дают четыре значения корней уравнения четвертой степени.

Если обозначить корни этих квадратных уравнений через $ x_1,x_2 $ и, соответственно, $ x_3,x_4 $, то они будут связаны с корнем $ t_ $ резольвенты Феррари равенством $ t_1=x_1x_2+x_3x_4 $. В самом деле, это равенство следует из двух формул Виета: $ x_1x_2=t_1/2-L,, x_3x_4=t_1/2+L $. Остальные корни резольвенты получаются в результате перестановок $ t_2=x_1x_3+x_2x_4,, t_3=x_1x_4+x_2x_3 $.

Пример [2]. Решить уравнение $ x^4+4,x-1=0 $ .

Решение. Здесь $ p=0,,q=4,r=-1 $ и резольвента Феррари имеет вид $$t^3+4,t-16=0 .$$ Последнее уравнение имеет корень $ t_1=2 $. Следовательно, исходное уравнение можно переписать в виде: $$ (x^2+1)^2 =left(sqrtx- sqrtright)^2 . $$ Оно распадается на два квадратных: $$ x^2+1=sqrt, x- sqrt u x^2+1=-sqrt, x + sqrt . $$

Видео:Уравнение 5-й степениСкачать

Преобразование Чирнгауза

Успех, достигнутый в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода была очевидна: свести решение уравнения $ n_ $-й степени к решению уравнения $ (n-1)_ $-й степени. Одну из возможных вариаций этого подхода поясним на примере.

Пример. Решить уравнение $ x^3+6,x-2=0 $.

Решение. Обозначим неизвестные корни полинома $ f(x)=x^3+6,x-2 $ через $ lambda_1,lambda_2, lambda_3 $. Построим полином $ F_(y) $, корнями которого являются величины $$ mu_j=lambda_j^2+2, lambda_j+4 . $$ Выражение $$F(y)= (y-mu_1)(y-mu_2)(y-mu_3)$$ является симметрическим полиномом относительно $ lambda_1,lambda_2 $ и $ lambda_ $. Следовательно, по теореме Гаусса о симметрических полиномах, коэффициенты $ F_(y) $ должны полиномиально выражаться через коэффициенты $ f_(x) $, т.е. быть числами целыми. Опуская промежуточные выкладки, приведем окончательный результат: $$F(y)equiv y^3-108 .$$ Корни этого полинома легко определить: $$ mu_1=3sqrt[3], mu_2= 3sqrt[3] left(-frac +mathbf i frac<sqrt> right), mu_3= 3sqrt[3]left(-frac -mathbf i frac<sqrt> right) . $$ Теперь находим $ lambda_ $ из квадратных уравнений $$sqrt[3] — sqrt[3], -2-sqrt[3] + sqrt[3], $$ $$ fracleft(-sqrt[3] + sqrt[3]right) + mathbf i frac<sqrt> left(sqrt[3] + sqrt[3]right), -2 + fracleft(sqrt[3] — sqrt[3]right) — mathbf i frac<sqrt> left(sqrt[3] + sqrt[3]right), $$ $$ fracleft(-sqrt[3] + sqrt[3]right) — mathbf i frac<sqrt> left(sqrt[3] + sqrt[3]right), -2 + fracleft(sqrt[3] — sqrt[3]right) + mathbf i frac<sqrt> left(sqrt[3] + sqrt[3]right). $$ Подстановкой в исходное уравнение выделяем истинные его корни.

Подобное преобразование полинома $ f_(x) $ в полином $ F_(y) $ той же степени, имеющий корнями числа $ g(lambda_1),dots, g(lambda_n) $ при произвольном полиноме $ g(x)in mathbb A[x] $, называется преобразованием Чирнгауза.

Биографические заметки о Чирнгаузе ☞ ЗДЕСЬ.

Задача. Найти такое преобразование Чирнгауза, которое преобразует исходный полином к виду $ y^n-a $. Корни последнего, очевидно, выражаются в радикалах. Если при этом, $ deg g ♦

Следующий способ нахождения преобразования Чирнгауза является развитием метода Безу вычисления результанта.

Найдем остатки от деления $ x^kg(x) $ на $ f_(x) $ $$ g_k(x) = b_+b_x+dots +b_x^+b_x^ quad npu quad kin $$ (здесь изменен порядок нумерации коэффициентов по сравнению с тем, что указан при изложении ☞ метода Безу ) и составим матрицу из коэффициентов: $$ B=[b_]_^ . $$

Теорема [Эрмит]. Имеем:

Доказательство. Равенства $$y=g(x),, xy=g(x)x,, dots, x^y=g(x)x^ ,$$ при подстановке корня $ lambda_j $ полинома $ f(x) $ переходят в $$y=g_0(lambda_j),,lambda_jy=g_1(lambda_j),dots, lambda_j^y=g_(lambda_j) .$$ Рассмотрим получившиеся уравнения как линейную однородную систему относительно столбца неизвестных $$X=[1,lambda_j,dots,lambda_j^]^ . $$ Поскольку эта система имеет нетривиальное решение, то (на основании следствия к теореме Кронекера-Капелли ) определитель ее матрицы должен обращаться в нуль. ♦

Пример. Решить предыдущий пример по методу Эрмита.

Решение. Имеем $$g_0(x)equiv g(x)=-1+x+x^2, g_1(x)=-3+x+x^2, g_2(x)=-3-x+x^2 $$ и, следовательно, $$F(y)=(-1)^3left| begin -1-y & 1 & 1 \ -3 & 1-y & 1 \ -3 & -1 & 1-y endright|=y^3-y^2+6,y-4 . $$

Будем решать теперь вторую из сформулированных выше подзадач: подобрать преобразование Чирнгауза таким образом, чтобы обнулить как можно большее число коэффициентов у полинома $ F_(y) $.

Пример. Для полинома $ f(x)=x^3+a_1x^2+a_2x+a_3 in mathbb C[x] $ подобрать преобразование Чирнгауза вида $ y=x^2+b_1x+b_2in mathbb C[x] $ так, чтобы получившийся в результате преобразования полином имел вид $ F(y)=y^3+c_3 $.

Найти преобразование Чирнгауза, позволяющее решить в радикалах уравнение $ x^3+a_1x^2+frac, a_1^2x+a_3=0 $.

Статья не закончена!

Видео:9 класс. Алгебра. Решение уравнений 5 степени.Скачать

Разрешимость в радикалах

Успех достигнутый в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода очевидна из предыдущих пунктов: свести решение уравнения $ n_ $-й степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков мира, решить уравнение пятой степени не удавалось. Наконец, в начале XIX века был получен отрицательный результат.

Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем случае неразрешимо в радикалах.

Пример. Уравнение $ x^5-4, x -2=0 $ неразрешимо в радикалах.

Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.

Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку $ x^5+x+1equiv (x^2+x+1)(x^3-x^2+1) $.

Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде формулы, состоящей из конечного набора сравнительно простых функций. Тем не менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти. Cм., к примеру,

Наконец, для практических задач часто более важна не столько «красивая» аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.

Видео:Формула для уравнения пятой степениСкачать