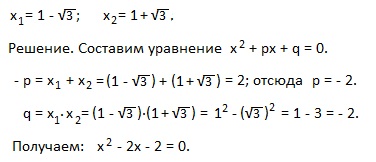Уравнение 2x2 px q 0 имеет корни 1 и 6 найдите p (2 видео)

Уравнение x ^ 2 + px + q = 0 имеет корни — 5 и 4 найдите p?

Математика | 5 — 9 классы

Уравнение x ^ 2 + px + q = 0 имеет корни — 5 и 4 найдите p.

Должно быть как — то так.

Содержание

Сколько корней имеет уравнение ?
8) квадратное уравнение, корни которого на 4 единицы меньше корней уравнения = 0, имеет вид ?
Сколько корней имеет уравнение?
Для квадратного уравнение 2х² + 10х + с = 0 выберите верные утверждение : 1)?
Имеет ли корни уравнение а3 = а : а?
Имеет ли корни уравнение : а — а = а•a?
Уравнение , которое имеет 6 корней ?
Как узнать, какое уравнение имеет один корень, какое не имеет корней и какое имеет бесконечное множество корней?
Сколько корней имеет уравнение?
Может ли уравнение не имеет ни одного корня?
Имеет ли корни уравнение у3 = у * у?
8.2.3. Теорема Виета
🎦 Видео

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Сколько корней имеет уравнение ?

Видео:Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

8) квадратное уравнение, корни которого на 4 единицы меньше корней уравнения = 0, имеет вид ?

8) квадратное уравнение, корни которого на 4 единицы меньше корней уравнения = 0, имеет вид .

Видео:Алгебра. 8кл. ДМ. К-5. В1. Пример №3. В уравнении x^2+px-18=0 один из его корней равен -9...Скачать

Сколько корней имеет уравнение?

Сколько корней имеет уравнение.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Для квадратного уравнение 2х² + 10х + с = 0 выберите верные утверждение : 1)?

Для квадратного уравнение 2х² + 10х + с = 0 выберите верные утверждение : 1).

При с = — 0, 5 уравнение имеет корни 2).

При с = 0 уравнение не имеет корней 3).

При с = 12, 5 уравнение имеет один корень 4).

При с = 24 уравнение не имеет корней 5) при с = 8уравнение не имеет корней Прошу виберите три правильных ответов.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Имеет ли корни уравнение а3 = а : а?

Имеет ли корни уравнение а3 = а : а.

Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Имеет ли корни уравнение : а — а = а•a?

Имеет ли корни уравнение : а — а = а•a.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Уравнение , которое имеет 6 корней ?

Уравнение , которое имеет 6 корней .

Уравнение , которое имеет бесконечное множество корней.

Уравнение , которое не имеет корней .

Видео:№1 Квадратное уравнение х^2+x-6=0 Дискриминант, теорема ВиетаСкачать

Как узнать, какое уравнение имеет один корень, какое не имеет корней и какое имеет бесконечное множество корней?

Как узнать, какое уравнение имеет один корень, какое не имеет корней и какое имеет бесконечное множество корней?

Видео:Теорема Виета. Алгебра, 8 классСкачать

Сколько корней имеет уравнение?

Сколько корней имеет уравнение.

Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

Может ли уравнение не имеет ни одного корня?

Может ли уравнение не имеет ни одного корня.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Имеет ли корни уравнение у3 = у * у?

Имеет ли корни уравнение у3 = у * у.

Перед вами страница с вопросом Уравнение x ^ 2 + px + q = 0 имеет корни — 5 и 4 найдите p?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Сначала решаешь скобку, потом по порядку слева направо.

1) 40 + 15 = 55 2) 55 + 20 = 75 3)75 — 21 = 54.

900 — (600 — 130 * 4) : 10 = 900 — (600 — 520) : 10 = 900 — 80 : 10 = 900 — 8 = 882 800 — 250 + 140 : 5 * 2 = 800 — 250 + 140 : 10 = 800 — 250 + 14 = 550 + 14 = 564.

Самое большое число, кратное 6 и при этом не больше 50 — это 48 Ответ : 48.

— 2, 5(3 — а) + 5(а — 7) = — 7, 5 + 2, 5а + 5а — 35 = (2, 5а + 5а) — (7, 5 + 35) = = 7, 5а — 42, 5.

8 + 4 = 12 (всего коробок) 480 : 12 = 40 шаров в одной коробке 8 * 40 = 320 красных шаров всего.

Например тетрадь 5 рублей А альбом на 3 рублей дороже чем тетрадь Ручка на 1 рубль дешевле чем альбом 1 )5 + 3 = 8 стоит альбом 2) 8 — 1 = 7 стоит ручка Вопрос сколько стоит альбом и ручка Ответ 8 рублей стоит альбом, а 7 рублей стоит ручка.

Тетрадь в клетку стоит 30 руб. Альбом на 40руб дороже чем тетрадь. А ручка на 50 руб дешевле чем альбом . Вопрос : Сколько стоит ручка? _____________________________ 1)30 + 40 = 70(руб) — Стоит альбом 2)70 — 50 = 20(руб) — Стоит ручка Ответ : 20р..

. Пусть коробок с бокаламипо 3штуких. Тогда остальных коробок (с бокаламипо 2штуки)12 — х. Составим уравнение для общего количества бокалов. Х·3 + (12 — х)·2 = 28 3х + 24 — 2х = 28 3х — 2х = 28 — 24 х = 4 Ответ : 4 коробки. Проверка. 4 коробки с..

Жила — была тройка. Как — то раз пошла она в соседнее королевство. Встретила она пятерку. Они обнялись и получилась восьмерка! Конец, а кто слушал молодец.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

8.2.3. Теорема Виета

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x 2 -x-30=0. Это приведенное квадратное уравнение ( x 2 +px+q=0), второй коэффициент p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121=11 2 .

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:

x₁+x₂=1; x₁∙x₂=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.

Пример 2) x 2 +6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=3 2 -1∙8=9-8=1=1 2 . Дискриминант D₁ является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x 2 +2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=1 2 -1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x₁=-7, x₂=4.

Решение. Искомое уравнение запишется в виде: x 2 +px+q=0, причем, на основании теоремы Виета –p=x₁+x₂=-7+4=-3 → p=3; q=x₁∙x₂=-7∙4=-28. Тогда уравнение примет вид: x 2 +3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax 2 +bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

Пример 6). Найти сумму корней квадратного уравнения 2x 2 -7x-11=0.

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7 2 -4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

Пример 7). Найдите произведение корней квадратного уравнения 3x 2 +8x-21=0.

Решение.

Найдем дискриминант D₁, так как второй коэффициент (8) является четным числом. D₁=4 2 -3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x₁∙x₂=c:a=-21:3=-7.