Уравнение 1 закона термодинамики в дифференциальном виде (4 видео)

Первый закон термодинамики в дифференциальном виде.

Формула для расчёта механической работы

при изменении объёма системы

Выражение (8.2) можно рассматривать как интегральную форму записи первого закона термодинамики.

Анализировать различные термодинамические процессы удобно, если пользоваться не интегральной, а дифференциальной формой записи первого закона термодинамики. В частности, это даёт возможность рассчитывать величину l – удельную работу процесса или, более строго, удельную энергию, подведённую к системе или отведённую от неё в форме механической работы.

Дифференциальная форма записи справедлива только для равновесных процессов. Рассмотрим её вывод из (8.2) для произвольного равновесного процесса изменения объёма некоторой термодинамической системы. Такой системой, в частности, может быть некоторый объём газа.

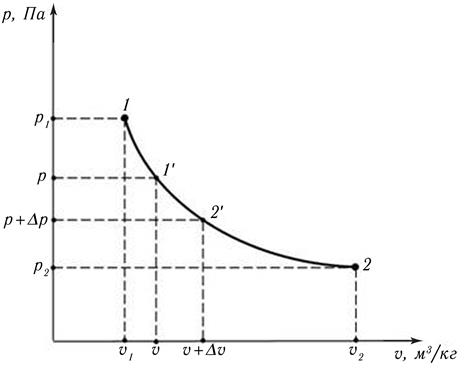
Известно, что равновесный процесс может быть изображён непрерывной кривой, например, в рυ – координатах (рис. 9.1). Это будет р = р (υ) – уравнение процесса, описывающее зависимость абсолютного давления системы р, Па, в ходе процесса, от удельного объёма υ, м 3 /кг.

Рис. 9.1. Равновесный процесс в рυ – координатах

Для некоторой системы, в которой реализуется процесс 1 – 2, первый закон термодинамики (8.1) запишется в виде:

На кривой р(υ) выберем произвольную промежуточную точку 1′ с параметрами р и υ. Рассмотрим малую часть процесса 1 – 2 в районе точки 1′, т.е. процесс 1′ – 2′, при котором параметры состояния изменяются на малые величины Δр и Δυ.

Для малого процесса 1′ – 2′ запишем первый закон термодинамики в виде:

где U и U +ΔU – внутренние энергии системы в точках 1′ и 2′ соответственно, Дж; ΔU – изменение внутренней энергии системы в процессе 1′ → 2′, Дж; ΔQ – теплота процесса 1′ – 2′, Дж; ΔL – работа процесса 1′ – 2′, Дж.

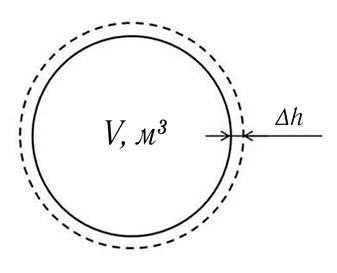
Для определения ΔL схематично изобразим систему в точках 1′ (сплошная линия) и 2′ (пунктирная линия) на рис. 9.2.

Рис. 9.2. Схема процесса 1′ – 2′:

V – объём системы в точке 1′; Δh – перемещение поверхности системы в процессе 1′ – 2′

Исходя из определения механической работы, можем записать:

, (9.4)

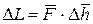
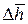
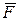
где – среднее перемещение поверхности системы в малом процессе 1′ – 2′, м; – среднее, за время малого процесса 1′ → 2′, значение силы, действующей на поверхность системы, Н.

В силу малости процесса 1′ – 2′, можем записать:

, (9.5)

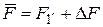
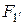
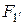
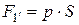
где – значение силы, действующей на поверхность системы в точке 1′, Н; ΔF – малое приращение, обусловленное изменениями давления и поверхности системы в ходе процесса 1′ – 2′, Н.

Значение определяется по очевидной формуле, при известных давлении системы р, Па, и площади поверхности системы S, м 2 , в точке 1′:

. (9.6)

Подставляя (9.5) и (9.6) в (9.4) получаем:

. (9.7)

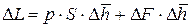
В (9.7) перейдём к пределу при Δр (а значит и Δυ) стремящемся к нулю:

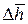
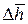
lim ΔL = p · S · lim + lim (ΔF · ).

В результате, отбросив по очевидным причинам бесконечно малые величины второго порядка малости, получаем:

, (9.8)

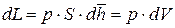
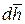
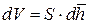
где dL – дифференциал механической работы в процессе 1 – 2, Дж; – дифференциал среднего перемещения поверхности системы в ходе процесса 1 – 2, м; dV – дифференциал изменяющегося в ходе процесса 1 – 2 объёма системы, , м 3 .

Замечание:

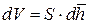
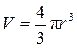
Для наглядности проиллюстрируем справедливость выражения для частного случая, когда система имеет сферический объем:

. (9.9)

Будем считать, что сфера «раздувается», то есть её радиус изменяется. После дифференцирования (9.9) получаем формулу для бесконечно малого приращения объёма «раздувающейся» сферы:

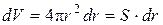
где S – площадь сферы, м 2 ; dr – дифференциал (бесконечно малое приращение) радиуса сферы, м.

Переходя в (9.3) к пределу при Δр (и Δυ) стремящихся к нулю и подставляя (9.8) будем иметь:

где dU, dQ и dL – дифференциалы (бесконечно малые приращения) внутренней энергии системы, теплоты и работы процесса соответственно, Дж.

Выражение (9.10) является дифференциальной формой записи первого закона термодинамики.

Разделив обе части (9.10), например, на массу системы, получаем уравнение для удельных величин:

где dυ – дифференциал удельного объема системы, м 3 /кг.

Таким образом, удельная механическая работа рассчитывается путём интегрирования дифференциального уравнения вида:

где р = p(υ) – уравнение процесса. В примере, изображённом на рис. 9.1. это процесс 1 – 2.

После интегрирования (9.12) от начала в точке 1 до конца процесса в точке 2 получаем формулу для расчёта удельной работы любого процесса 1 – 2:

. (9.13)

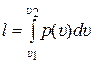
где υ₁ и υ₂ – значения удельного объёма в начале и конце процесса 1 – 2 соответственно, м 3 /кг.

Из геометрической интерпретации интеграла следует, что значение удельной работы, рассчитываемое по (9.13), равно площади под уравнением процесса р(υ) в рυ – координатах. На рис. 9.1 это площадь под линией процесса 1 – 2.

Для того чтобы по формуле (9.13) вычислить значение удельной работы необходимо знать вид функции р(υ) и пределы интегрирования υ₁ и υ₂.

Содержание

Первый закон термодинамики
Определение 1 -го закона термодинамики
Первый закон термодинамики в процессах газов
Первое начало термодинамики
Интегральная форма первого начала термодинамики
Готовые работы на аналогичную тему
💡 Видео

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Первый закон термодинамики

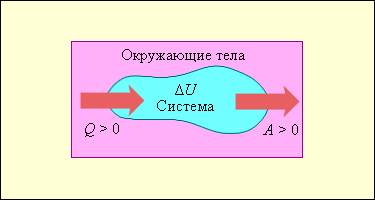
На рисунке 3 . 9 . 1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q > 0 , если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A > 0 .

Рисунок 3 . 9 . 1 . Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы Δ U .

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Определение 1 -го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Видео:Первый закон термодинамики. 10 класс.Скачать

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В изохорном процессе, то есть в условиях неизменного объема ( V = c o n s t ) , газ не совершает работы, A = 0 .

В этом случае справедливой будет формула внутренней энергии газа:

Q = ∆ U = U ( T 2 ) — U ( T 1 ) .

В данном выражении U ( T 1 ) и U ( T 2 ) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло ( Q > 0 ) , чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам ( Q 0 ) .

В изобарном процессе, предполагающем постоянность значения давления ( p = c o n s t ) , работа, совершаемая газом, выражается в виде соотношения:

A = p ( V 2 — V 1 ) = p ∆ V .

Первый закон термодинамики для изобарного процесса дает:

Q = U ( T 2 ) — U ( T 1 ) + p ( V 2 — V 1 ) = ∆ U + p ∆ V .

При изобарном расширении Q > 0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q 0 тепло переходит внешним телам. В таком случае A 0 . При изобарном сжатии уменьшаются температура газа T 2 T 1 и значение внутренней энергии Δ U 0 .

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0 .

Первый закон термодинамики для изотермического процесса выражается соотношением

Теплота Q , приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

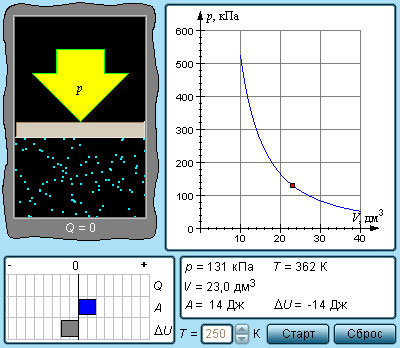
Рисунок 3 . 9 . 2 . Модель адиабатического процесса.

В адиабатическом процессе Q = 0 . По данной причине первый закон термодинамики принимает вид:

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Расширение или сжатие газа на плоскости p , V проиллюстрирована кривой, называемой адиабатой.

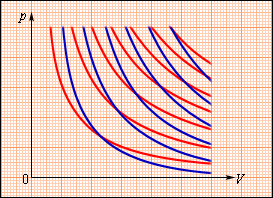
В процессе адиабатического расширения газом совершается положительная работа A > 0 , что является причиной понижения значения внутренней энергии Δ U 0 . Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3 . 9 . 3 ).

Рисунок 3 . 9 . 3 . Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат ( p , V ) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид:

p V γ = c o n s t .

Данное выражение, в котором γ = C p C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ = 5 3 = 1 , 67 , двухатомного γ = 7 5 = 1 , 4 , многоатомного γ = 1 , 33 .

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

A = C V ( T 2 — T 1 )

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу Δ Q T . Так как на каждом участке адиабатического процесса Δ Q = 0 , энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

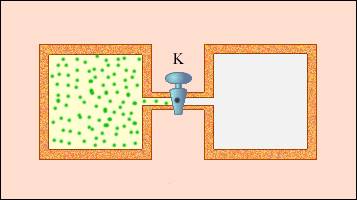
Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3 . 9 . 3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q = 0 , по той причине, что исключен теплообмен с окружающими телами, и A = 0 , так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что Δ U = 0 , то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости ( p , V ) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Рисунок 3 . 9 . 4 . Расширение газа в пустоту.

Видео:Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Первое начало термодинамики

Вы будете перенаправлены на Автор24

Закон сохранения энергии для количества теплоты как формы энергии может быть записан в виде:

[delta Q=dU+delta A left(1right).]

[CdT=dU+delta A left(2right),]

где C — теплоемкость системы.

В термодинамике уравнение (1) является крайне важным и называется первым началом. В отличие от закона сохранения их механики, первое начало термодинамики содержит бесконечно малое количество теплоты $delta Q$. Мы знаем, что изучение разного рода переходов именно этой формы энергии — предмет термодинамики. Очень часто уравнение (1) записывается в виде:

[delta Q=dU+pdV left(3right).]

Уравнения (1), (2) и (3) записаны в дифференциальной форме.

В связи с тем, что теплота и работа не являются функциями состояния, то для бесконечно малого количества теплоты и элементарной работы используют обозначение $delta Q$, а не $dQ$ и $delta A$, а не $dA$. Этим подчёркивается, что $delta Q$ и $delta A$ не рассматриваются как полные дифференциалы, т.е. невсегда могут быть представлены как бесконечно малые приращения функций состояния (только в частных случаях).

Первое начало термодинамики не может предсказать направление развития процесса. Этот закон лишь констатирует факт изменения величин в процессе и говорит о величине их изменения. Забегая вперед, скажем, что второе начало термодинамики определяет направление процесса.

В том случае, если рассматривается круговой процесс (система возвращается в исходное состояние), изменение внутренней энергии системы $dU=0$, то первое начало термодинамики говорит о том, что все тепло, которое получила система, идет на совершение этой системой работы.

Видео:Первый закон термодинамики. Применение первого закона терм-ки к изопроцессам. Практ. ч. 10 класс.Скачать

Интегральная форма первого начала термодинамики

Первое начало термодинамики можно записать и в интегральной форме:

[Q=triangle U+A left(4right).]

На словах уравнение (4) означает, что подводимая к системе теплота идет на изменение внутренней энергии системы и совершение этой системой работы.

Обратимся опять к круговому процессу ($triangle U$). Если в круговом процессе $Q=0, то A=0.$ Это означает, что невозможен процесс производства работы без какого-то ни было изменения во внешних к системе телах. Или говорят по-другому: не возможен вечный двигатель первого рода.

Рассмотрим изохорный процесс. При постоянном объеме система работу не совершает. В таком случае:

говорят, что все подводимое к системе тепло идет на изменение (увеличение) внутренней энергии системы.

В изотермическом процессе внутренняя энергия системы неизменна, следовательно:

все подводимое системе тепло идет на совершение системой работы.

Задание: В идеальном газе совершается процесс заданный уравнением: $T=T_0e^$, где $T_0, a- $ постоянные. Изохорная молярная теплоемкость газа $c_$ известна. Найти $c_$(V) для заданного процесса.

Основой для решения будет первое начало термодинамики в дифференциальном виде:

[CdT=dU+delta A left(1.1right).]

Приращение внутренней энергии $dU$ равно:

[dU=fracnu RdT to CdT=fracnu RdT +pdVleft(1.2right),]

Используем для дальнейших вычислений уравнение Менделеева — Клайперона:

Подставим в (1.3) вместо T уравнение процесса, получим:

[pV=nu RT_0e^to p=nu RT_0frac<e^> left(1.4right).]

Так как из уравнения процесса $dT$ равно:

То, подставив (1.5) и (1.4) в (1.2), получим выражение:

Соответственно, для молярной теплоемкости процесса получим:

Ответ: Молярная теплоемкость для заданного процесса выражается формулой: $c_left(Vright)=c_+frac$.

Готовые работы на аналогичную тему

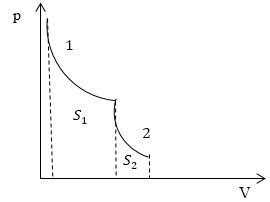
Задание: На рис.1 представлен процесс, состоящий из изотермы (1) и адиабаты (2). Укажите площадь, которая представляет количество теплоты, которое поглощает газ.

Запишем первое начало термодинамики в интегральном виде:

[Q=triangle U+A left(2.1right).]

Первая часть процесса, который представлен на рис.1, является изотермой, следовательно: $triangle U_1=0$ и уравнение (2.1) запишется, как:

Вторая часть процесса представлена адиабатой. Относительно адиабатных процессов известно, что они проводятся без подвода тепла, следовательно:

а работа по расширению газа идет за счет уменьшения его внутренней энергии.

Итак, мы получили, что в указанном на рис.1 процессе тепло подводится только на участке 1, и оно равно работе, которую совершает газ в процессе своего расширения. По определению в процессе 1 работа равна:

Из геометрического свойства интеграла $A_1=S_1$ на рис. 1.

Ответ: Количество теплоты, подведенное в заданном процессе, представлено площадью $S_1$ на рис. 1.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 11 2021