Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно рк.
В момент времени t = 0 скважина пущена в эксплуатацию с постоянным объемным дебитом Q0. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) р(r, t) определяется интегрированием уравнения (5.27):
, (5.49)
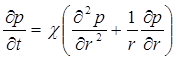
Начальные и граничные условия задачи следующие (см. гл. 2, § 7):
= Q 0 = const при r = 0, t > 0. (5.50)
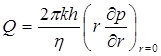
Последнее условие запишем в виде
. (5.51)
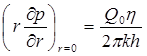
Так же, как в предыдущем случае, проведем анализ размерностей. Искомое распределение давления в пласте зависит от пяти определяющих параметров: r, t,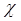 
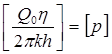
, pk,, Q 0η/(2πkh), размерности которых следующие:
,
где [p],-размерность давления. Тогда давление, приведенное к безразмерному виду, Р = р/рк зависит от двух безразмерных параметров (так как из пяти параметров три имеют независимые размерности (r, t, pк): n = 5, k = 3, n — k = 2.
Таким образом задача автомодельна и уравнение (5.49) можно свести к обыкновенному. Продифференцировав (5.52), найдем аналогично предыдущему:
,
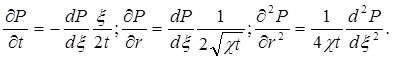
Подставив эти выражения в уравнение (5.49), получим обыкновенное дифференциальное уравнение вида
, (5.53)
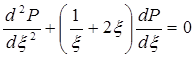
которое нужно проинтегрировать при условиях, полученных из (5.50) Р = 1 при ξ → ∞.
. (5.54)
,
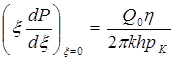
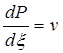
тогда вместо уравнения (5.53) будем иметь
. (5.55)
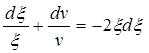
Проинтегрировав (5.55), получим:
, (5.56)
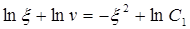
где C1-постоянная интегрирования.
Потенцируя (5.56), получим:
, (5.57)
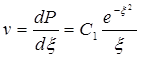
Проинтегрировав (5.57), и учтя первое из условий (5.54), получим:
, (5.58)
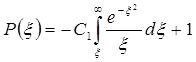
Умножая равенство (5.57) на ξ устремляя ξ → 0 и используя второе условие (5.54), найдем, что
.
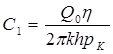
Тогда из (5.58) получим:
. (5.59)
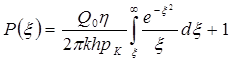
Интеграл в последней формуле легко свести к табличному следующий подстановкой:
,
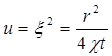
тогда
.
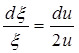
Перейдя также от безразмерного давления Р к размерному р = Ррк получим:
. (5.60)
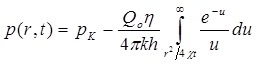
Интеграл в формуле (5.60) называется интегральной показательной функцией, которая табулирована и обозначается
.
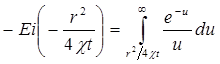
Следовательно, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле
. (5.61)
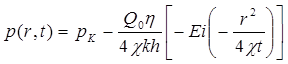
Формула (5.61) получила название основной формулы теории упругого режима фильтрации. Она имеет широкое практическое применение и, в частности, используется при интерпретации результатов исследования скважин, в расчетах распределения давления при фильтрации упругой жидкости и т.д.
Интегральную показательную функцию можно представить в виде ряда
,
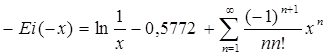
который сходится при всех значениях х 0
.
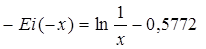
При этом погрешность не превосходит:
 |
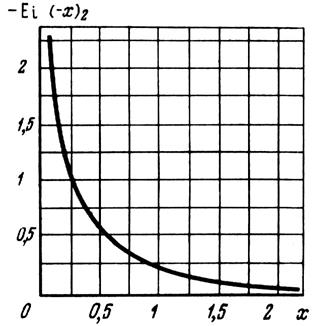Рис. 5.3. График интегральной показательной функции
0,25% если х =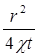 
≤ 0,01;
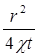
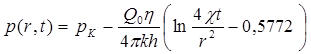
Следовательно, для значений ≤ 1 давление можно определять по формуле
. (5.62)
Из (5.61) находим, что расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соответственно по формулам
, (5.63)
. (5.64)
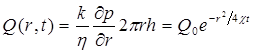
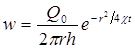
Из последней формулы следует, что стационарная скорость wстац =
=Q0/(2πrh) достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности обычно велико.
При теоретическом исследовании неустановившихся процессов перераспределения пластового давления удобно пользоваться безразмерными параметрами Фурье fo и Fo, играющими роль безразмерного времени и определяемыми по следующим равенствам:
, (5.65)
 |
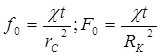
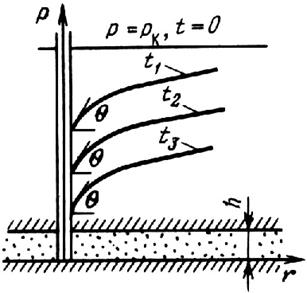Рис. 5.4. Пьезометрические кривые при пуске скважины с постоянным дебитом Q0
где rc — радиус скважины; Rк, — радиус кругового контура питания или радиус круговой непроницаемой границы пласта.
В зависимости от специфики решаемой задачи удобно пользоваться тем или другим из указанных параметров Фурье.
Строго говоря, основная формула теории упругого режима (5.61) справедлива лишь для случая точечного стока (при rc = 0) в неограниченном пласте (Rк = ∞).
Для оценки влияния конечного радиуса возмущающей скважины rc на результаты расчетов давления В. Н. Щелкачев сравнил результаты расчетов давления по формуле (5.61) с точной формулой Ван-Эвердингена и Херста (см. § 8), учитывающей конечный радиус скважины rc. При этом В. Н. Щелкачев установил, что погрешность подсчетов давления по формуле (5.61) составляет:
Оценим практическое значение этой погрешности. Допустим, что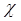 
= 1 м 2 /с, rc = 0,1 м; тогда полагая fo = 100, найдем:
Следовательно, уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (5.61), будут иметь погрешность, не превышающую 0,6%. Отсюда следует, что для скважин обычных размеров формула (5.61) обеспечивает высокую степень точности уже на самой ранней (а тем более на поздней) стадии процесса перераспределения давления.
Непосредственными расчетами В. Н. Щелкачевым было установлено, что в громадном большинстве практически интересных случаев изменение давления при работе скважины в конечном открытом пласте можно в течение достаточно длительного времени изучать при помощи простой формулы (5.61) для бесконечного пласта. При этом погрешность в подсчетах забойного давления не превзойдет:
Для расчетов пластового давления в любой точке открытого кругового пласта в случае r ≤ 0,1 Rк можно с высокой степенью точности (до 0,2%) пользоваться формулой (5.61) для бесконечного пласта, если при этом Rк ≥10 5 rс , Fo ≤ 0,2.
В дополнение к указанным оценкам можно еще отметить, что различие в величинах забойных давлений в условиях конечного (открытого и закрытого) и бесконечного пластов не превзойдет 1%, если Fo ≤ 0,33, Rк ≥ 50 rс, или если Fo ≤ 0,35, Rк ≥ 1000 rс.
Решение дифференциального уравнения Фурье (5.49) для различных случаев фильтрации упругой жидкости в ограниченных открытых и закрытых пластах представляются бесконечными рядами по функциям Бесселя (см. § 8).
В заключение покажем, как ведут себя пьезометрические кривые вблизи скважины, которая эксплуатируется с постоянным дебитом Q0 (рис. 5.4). Для точек вблизи забоя можно пользоваться формулой (5,62); продифференцировав ее по координате r, найдем градиент давления:
.
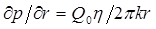
Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r 2 ≤ 0,03 • 4 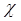t, практически не зависит от времени и определяется по той же формуле, что для установившейся плоскорадиальной фильтрации несжимаемой жидкости. Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (см. рис. 5.4). Давление на забое скважины падает с течением времени, углы наклона касательных θ на забое одинаковы для всех кривых.
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОГО РЕЖИМА
Решения различных краевых задач неустановившейся фильтрации упругой жидкости в упругой пористой среде в условиях как бесконечного, так и конечного пластов можно получить при помощи хорошо известных методов интегрирования линейного дифференциального уравнения в частных производных-уравнения теплопроводности (5.14).
Однако во многих случаях эти решения представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции.
В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации.
Рассмотрим здесь некоторые из разработанных приближенных методов, получивших широкое применение при решении задач теории упругого режима.
Видео:Лабораторная работа 5 Определение коэффициента фильтрации в приборе ПКФ СДСкачать
Добыча нефти и газа
Видео:Задачи линейной фильтрации и оценки параметров для процессов типа "дробного Броуновского движения"Скачать
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Видео:ЦОС Python #6: Фильтр Калмана для авторегрессионого уравненияСкачать
Понятия об упругом режиме пласта
При разработке нефтегазовых месторождений часто возникают неустановившиеся процессы, связанные с пуском или остановкой скважин, с изменением темпов отбора флюидов из скважин. Характер этих процессов проявляется в перераспределении пластового давления, в изменениях во времени скоростей фильтрации, дебитов скважин и т.д. Особенности данных процессов зависят от упругих свойств пластов и жидкостей, т.е. основная форма пластовой энергии — энергия упругой деформации жидкостей и материала пласта.
Упругий режим характеризуется двумя особенностями:
* неустановившимися процессами перераспределения давления в пласте;
* изменением упругого запаса жидкости в пласте.
При упругом режиме движение возникает в призабойной зоне в начале эксплуатации скважины за счет использования потенциальной энергии упругой деформации пласта и жидкости и только через некоторое время оно распространяется на более отдалённые области.
При снижении пластового давления объём сжатой жидкости увеличивается, а объём порового пространства сокращается за счет расширения материала пласта. Всё это способствует вытеснению жидкости из пласта в скважину.
В ряде случаев приток жидкости поддерживается за счет напора воды, поступающей извне. Такой режим называется упруговодонапорным.
Если залежи нефти ограничены либо зонами выклинивания, либо экранами, то режим называется замкнуто-упругим. В начальной стадии разработки такой залежи до тех пор, пока пластовое давление не снизилось ниже давления насыщения, имеет место замкнуто-упругий режим фильтрации.
Если вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости, то упруговодонапорный режим переходит в жестко-водонапорный режим. При этом режиме влияние упругости пласта и жидкости на фильтрационный поток хотя и не прекращается, но заметно не проявляется.
Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k, и тем медленнее, чем больше вязкость жидкости m и коэффициенты объёмной упругости жидкости и пласта.
4.1.2. Основные параметры теории упругого режима
Важнейшими параметрами теории упругого режима являются коэффициенты объёмной упругости жидкости и пласта.
Коэффициент объёмной упругости жидкости bж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу
, (4.1)
где tж — объём жидкости; знак минус указывает на то, что объём tж увеличивается с уменьшением давления; bж нефти находится в пределах (7-30)10-10м2/н; bж воды находится в пределах (2,7-5)10-10м2/н.
Коэффициент объёмной упругости пласта определяется по формуле
, (4.2)
где tп — объём пласта; m — пористость; bС слабо и сильно сцементированных горных пород находится в пределах (0,3-2)10-10м2/н.
Большое значение в практике добычи нефти и подсчета её запасов имеет величина упругого запаса выделенной области пласта, соответствующая заданному падению давления. По Щелкачеву упругий запас — это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта.
Обозначая упругий запас через Dtз , получаем по определению
Dtз = bжt0жDр + bсt0Dр, (4.3)
где t0ж — объём жидкости, насыщающей элемент объёма пласта t0 при начальном давлении р0; Dр — изменение давления.
Так как t0ж = mt0, то
Здесь b* = mbж + bс — коэффициент упругоёмкости пласта, показывающий долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу.
Вскрытие пласта и изменение режима работы скважины вызывает возмущение в пласте. От источника возмущения оно передаётся во все стороны пласта с какой-то скоростью. Скорость распространения изменения пластового давления характеризуется коэффициентом пьезопроводности пласта
. (4.5)
Здесь L, T –размерности длины и времени.
В коллекторах – 1000см2/с £ k £ 50000см2/c или 0.1м2/с £k £5м2/c.
Степень нестационарности процессов определяется безразмерными параметрами Фурье:
для призабойной зоны — 
; (4.6)
для всего пласта 
, (4.7)
4.1.3. Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности)
Считаем, что течение происходит по закону Дарси, и уравнение состояния упругой жидкости в линеаризованной постановке, которое получим из соотношения (2.27) разложением экспоненты в ряд Тейлора, имеет вид
, (4.8)
а также изменение пористости в зависимости от давления, полученное линеаризацией соотношения (2.34), описывается зависимостью
. (4.9)
Из (4.9) и очевидного соотношения 
имеем следующее дифференциальное уравнение для пористости, при пренебрежении членом, содержащим произведение bжbс
. (4.10)
В то же время из общего уравнения фильтрации (2.8) 
.
Приравнивая правые части, с учетом выражения для потенциала 
, и пренебрегая членом, содержащим (р-р0)2, получим
. (4.11)
Уравнение типа (4.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент k характеризует быстроту распределения давления в пласте и носит название коэффициент пьезопроводности. Само уравнение (4.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.
4.1.4. Приток к скважине в пласте неограниченных размеров
4.1.4.1. Вывод основного уравнения упругого режима
Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).
Рассмотрим процесс перераспределения давления при неустановившемся, плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат
. (4.12)
Предположим, что возмущение вызвано мгновенным стоком, существовавшим в момент t = t/ . Для этого случая решение уравнения (4.12) имеет вид
, (4.13)
где А и С — некоторые постоянные.
Найдём значения постоянных. Для этого будем считать, что в момент времени t = t/ давление в пласте было р = рк = const. Тогда при r > 0 и при t = t/ второй член правой части обращается в неопределённость типа ¥/¥ и определяется по правилу Лопиталя, что даёт С = рк. Таким образом,
. (4.14)
Для определения коэффициента А воспользуемся соотношением (4.4) для определения объёма высвобождающейся жидкости для случая кольцевого элемента пласта с внутренним радиусом r, толщиной h и шириной dr, а также учтем падение давления Dр = p0 — p по (4.14):
dtз = b*Dрdt0 = 
. (4.15)
После интегрирования (4.15) в пределах от 0 до ¥ получим объём жидкости t2 , выделившейся из всего пласта и, следовательно, определим коэффициент А:
. (4.16)
Таким образом в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением:
. (4.17)
Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q = Q0 в течение времени dt/, то за этот промежуток времени через сток выделяется из пласта объём
dt2 = Qdt/ и, следовательно, из (4.17) следует
. (4.18)
Интеграл правой части носит название интегрально-показательной функции
и с учетом данного обозначения решение для изменения давления запишется в виде
. (4.19)
Формула (4.19) является основной формулой теории упругого режима пласта.
Рис. 4.1. График интегрально — показательной функции
Интегрально-показательная функция имеет вид (рис.4.1) и обладает следующими свойствами:
* -Ei(-u) изменяется от 0 до ¥ при изменении аргумента от 0 до ¥;
* функция -Ei(-u) представляется в виде сходящегося ряда
(4.20)
Для малых значений u
, (4.21)
с погрешностью, не превышающей 0,25% при u
. (4.22)
С учетом соотношения (4.21) основное уравнение (4.19) перепишется в виде, которое более известно под названием уравнение кривой восстановления давления (КВД)
. (4.23)
Рис. 4.2. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом
Полученную зависимость можно использовать при числе Фурье 
с погрешностью, не превышающей 0,6%. Практически это означает, что уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (4.23), будут иметь погрешность не превышающую 0,6%. Формулу (4.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1%, если rк > 1000rc и fo
Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса rc c постоянным дебитом Q0 (рис.4.2). Для точек вблизи забоя можно пользоваться формулой (4.23), а дифференцируя её по координате r, найдём градиент давления
.
Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r2
4.1.4.2. Анализ основной формулы теории упругого режима
Основная формула (4.19) или (4.23) строго говоря справедлива лишь для точечного стока, т.е. при rс=0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин (rс
1км) и нельзя использовать только в первые доли секунды после пуска скважины. Если скважина укрупнённая, то формула (4.23) может дать большую погрешность лишь вблизи от её стенки (контура). Чем дальше отстоит от этого контура точка, в которой определяется давление, и чем больше времени прошло с момента пуска укрупнённой скважины, тем меньше погрешность.
Анализ формулы (4.23) показывает, что вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта (рис.4.2), в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т.е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа.
Из (4.23) следует, что градиент давления, расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соотношениями:
(4.24)
Из данных соотношений следует, что стационарная скорость 
достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности велико.
4.1.4.3. Приток к скважине в пласте конечных размеров в условиях упруго-водонапорного и замкнуто- упругого режима
Круглый горизонтальный пласт с открытой внешней границей
Рис. 4.3. . Пьезометрические кривые при пуске скважины в конечном пласте
с открытой внешней границей:
а — с постоянным дебитом;
b — с постоянным забойным давлением рс
Постоянный дебит. Пусть пласт имеет внешнюю границу радиусом rк, через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом rс, которая мгновенно запускается в эксплуатацию с постоянным дебитом Q0. Перед пуском скважины давление в пласте было рк.
Для определения давления используем полученную ранее зависимость
, (4.19)
для неограниченного пласта и формулу Дюпюи
(4.25)
для установившегося плоскорадиального потока. В результате совместного решения данных зависимостей получим следующую приближённую формулу
, (4.26)
Рис. 4.4. Изменение дебита скважины с течением времени при постоянном забойном давлении рс
где ру — установившееся давление в любой точке пласта или в реагирующей бездействующей скважине (давление ру соответствует времени t = ¥ или Fo = ¥ ).
Изменение пьезометрической кривой в различные моменты времени после пуска скважины с постоянным дебитом в пласте с круговым контуром питания показано на рис.4.3а.
Постоянное забойное давление. На рис 4.3b изображена в различные моменты времени пьезометрическая кривая после пуска возмущающей скважины с постоянным забойным давлением, на рис.4.4 — изменение дебита скважины с течением времени.
Круглый горизонтальный пласт с закрытой внешней границей
Рис. 4.4. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при
Постоянный дебит. Будем считать дебит скважины постоянным. Пьезометрические кривые падения давления для разных моментов времени показаны на рис. 4.4. С некоторого момента смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние d, т.е. во всех точках пласта давление падает с одной скоростью.
Из рассмотрения рис. 4.3, 4.4. видно, что в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией.
Кроме того, при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.
Если скважина действовала с постоянным дебитом при установившимся потоке и в некоторый момент времени она останавливается, то начинается процесс восстановления давления. Уровень жидкости в скважине начинает подыматься.
Для расчета используются полученные выше формулы для возмущающей скважины, но вместо данных понижения давления в пласте надо подставить данные повышения давления после остановки скважины.
Рис. 4.6. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении
Рис. 4.7. Изменение дебита Q (кр.1) скважины и суммар-ной добычи Qcp (кр.2) с течением времени t
Постоянное забойное давление. Объемный дебит возмущающей скважины определяется по формуле
(4.27)
а объем жидкости tж, добытой из скважины (в пластовых условиях) за время t с момента пуска скважины равен
.
При больших параметрах Фурье fo объем Qж оказывается равным упругому запасу жидкости в закрытом пласте
На рис. 4.6 показана пьезометрическая кривая для нескольких моментов времени в закрытом пласте, а на рис. 4.7 изображены две кривые: одна из них характеризует падение дебита скважины с постоянным забойным давлением (кр. 1); другая — рост суммарной добычи жидкости tж (кр.2).
4.1.4.4. Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами
Различают две группы гидродинамических методов: при установившихся и неустановившихся режимах. Первые связаны с теорией одномерного потенциального течения, а вторые — с теорией упругого режима. После пуска или остановки скважины происходит перераспределение давления, которое можно снять и получить кривую восстановления (КВД) или стабилизации (КСД) давления. На форму данных кривых влияют коллекторские свойства, что дает возможность определения таких параметров как проницаемость и пьезопроводность.
Наиболее распространен метод определения коллекторских свойств по данным о восстановлении забойного давления (КВД) в остановленных скважинах в полулогарифмических координатах (Dр, lnt) на основе зависимости (4.30), записанной относительно забоя скважины в виде
(4.34)
Уравнение (4.34) можно рассматривать как уравнение изменения забойного давления после остановки скважины, работающей до этого с постоянным дебитом Q.
Рис. 4.8. Кривая КВД
Уравнение (4.34) представляет собой прямую (рис. 4.8) в координатах Dрс-lnt, а коэффициент i определяется как тангенс угла её наклона j к оси времени и коэффициент А — как отрезок оси давления, отсекаемый продолжением прямой.
По известным коэффициентам можно определить коллекторские свойства пласта:
· по коэффициенту i определяют гидропроводность пласта
. (4.35)
· Если известна вязкость жидкости в пластовых условиях m и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта:
. (4.36)
· По известному угловому коэффициенту i = tgj и радиусу rc скважины из коэффициента А можно определить коэффициент пьезопроводности пласта.
Область применения указанных приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (4.34), а именно: скважина рассматривается как сток постоянной интенсивности в бесконечном однородном пласте , и возможна мгновенная остановка притока флюида в скважину.
В случае ограниченого пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД начинает искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой КВД ограничена.
Кроме того, в реальных условиях скважину нельзя остановить мгновенно. После её закрытия на устье приток флюида из пласта продолжается ещё некоторое время из-за упругости жидкостей и газов, заполняющих скважину. Время выхода на асимптоту должно, очевидно, превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует.
На форму КВД сказывается также несовершенство скважины и возможное нарушение закона Дарси у стенок скважины. В этом случае необходимо решение более сложного уравнения пьезопроводности с нелинейными членами и использование приближенных методов расчета коллекторских свойств.
Твердотопливные котлы в Украине котлы в Украине
Полное описание первых признаков и выраженных симптомов при гепатите В здесь
Видео:ХБП: расчет скорости клубочковой фильтрации. Первый вебинар цикла.Скачать
Лекция3 Упруг.реж.. Лекция3 Разработка нефтяных месторождений при упругом режиме
| Название | Лекция3 Разработка нефтяных месторождений при упругом режиме |
| Дата | 02.10.2021 |
| Размер | 121.72 Kb. |
| Формат файла |  |
| Имя файла | Лекция3 Упруг.реж..docx |
| Тип | Лекция #240314 |
 С этим файлом связано 1 файл(ов). Среди них: Алгоритм.docx. Показать все связанные файлы Подборка по базе: Курсовая работа — Разработка бизнес-плана.doc, ПЗ 05 Разработка на основе тестирования с помощью обозревателя т, ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА БАКАЛАВРА Тема_ Разработка про, методическая разработка урока по бисквитам.docx, 08.02 Разработка сценариев в приложениях MS Office с применением, 9_ Веб-дизайн и разработка WS.pdf, 2016 Разработка рекомендаций по совершенствованию государственно, ИССЛЕДОВАНИЕ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН.doc, Эксплуатация нефтяных и газовых месторождений.docx, Методическая разработка практического занятия по дисциплине _КонВидео:Лекция_Проницаемость_Закон_Дарси_09_10_2018Скачать  Лекция№3Разработка нефтяных месторождений при упругом режиме. Первая книга о режимах разработки пластов появилась в США под названием «Аналитические основы добычи нефти и воды из скважин». Ее автор – Стенли Геронд. На русском языке она была издана в 1932 г. Идея существования упругого режима разработки нефтяных пластов была высказана проф. И.Н.Стрижовым еще в 1920-х годах. В дальнейшем она была развита (в частности М. Маскетом) рядом зарубежных и отечественных исследователей. В настоящее время теория упругого режима разработки нефтяных залежей разработана достаточно трудами таких ученых как М. Маскет, Д. Шилсюиз, У. Херст, В.Н. Щелкачев, А.Т. Горбунов и др. Основным признаком упругого режима является однофазность фильтрационного потока, т.е. условие превышения пластового давления над давлением насыщения. Если упругие деформации считать квазилинейными и подчиняющимися закону Гука, полученному для однородного пласта, то можно записать: или в дифференциальной форме где V – объем упругого тела; Р – давление; β – коэффициент объемной упругости тела (сжимаемость). Объемная упругость нефти зависит от давления, температуры, ее фракционного состава и количества растворенного газа. Для условий месторождений России она изменяется в достаточно широких пределах – от Сжимаемость пластовых вод изменяется в небольших пределах от При наличии растворенного газа в минерализованной воде ее сжимаемость будет равна: где βв — упругость воды без растворенного газа, 1/Па; Сжимаемость горных пород зависит от условий залегания продуктивных пластов, величины горного давления и характера изменения напряженного состояния пород при разработке залежи. В диапазоне внешнего давления от 0 до 100 МПа величина сжимаемости горных пород изменяется в пределах от Упругий запас залежи. Под упругим запасом залежи понимается количество нефти (флюида), которое может быть извлечено за счет упругих сил пласта и пластовых флюидов. Упругий запас определяется расширением нефти, воды и породы при снижении давления. Аналитически, согласно закону Гука, можно записать: где Чтобы оценить численно возможности упругого режима рассмотрим следующий пример. Обозначения общепризнанные. Vп = 10 9 м 3 ; m = 0,2; βж = 10 -9 1/Па; βс = 10 -9 1/Па; Sн = 1,0; Коэффициент упругоемкости пласта равен Тогда нефтеотдача пласта при упругом режиме для принятых условий составляет 0,06 или 6%. Видно, что возможности упругого режима весьма незначительные. Упругий режим – это естественный режим истощения залежи. Гидродинамическая теория упругого режима впервые была разработана М. Маскетом, Д Шилсюизом и У Херстом в 1937 г. На начальном этапе создания теории упругого режима в работах М. Маскета и Т. Мура и других при определении упругоемкости пласта сжимаемостью породы пренебрегали и полагали, что Наиболее полно теория упругого режима дана профессором В.Н. Щелкачевым. Необходимость учета сжимаемости породы была им показана на основании результатов экспериментальных исследований Д.А. Антонова (1952 г.). К аналогичному выводу пришел и американский ученый Х.Холл в 1953 г. Упругие деформации могут быть обратимыми и необратимыми. Экспериментально это было подтверждено исследованиями В.М. Добрынина. Теоретическое описание было сделано Г.И. Баренблаттом и А.П. Крыловым и названо упруго-пластическим режимом (по определению проф. И.Н. Стрижова – упруго-грузовой режим). Дальнейшее развитие теории механизма этого процесса было дано В.Н.Николаевским и А. Т. Горбуновым. Изменение давления при упругом законе упругости описывается дифференциальным уравнением пьезопроводности по аналогии с известным уравнением теплопорводности Фурье, известным в математической физике с начала XIX века. Уравнение пьезопроводноси имеет вид: где æ – коэффициент пьезопроводности горной породы, характеризует распределения давления в пласте, предложен проф. В.Н. Щелкачевым по аналогии с коэффициентом температуропроводности в уравнении Фурье. Решение уравнения теплопроводности впервые получено Лапласом. Для плоско-радиальной фильтрации уравнение пьезопроводности имеет вид: с учетом инерционных сил: и в случае неизотермической фильтрации: где Такое решение уравнения пьезопроводности при определенных начальных и граничных условиях было получено Ван-Эвердингеном и У. Херстом виде интегрального выражения, куда входят функции Бесселя. Если обозначить нижеприведенное соотношение то при Разновидности упругого режима. e Упруго-замкнутый режим, который проявляется в замкнутых (изолированных от законтурной области) пластах; e Упруговодонапорный, который имеет место в залежах со значительной по размерам законтурной водоносной областью. При разработке нефтяных месторождений на упругом режиме выделяют две фазы: Первая фаза существует до тех пор, пока возмущение от пуска скважины в работу, не достигнет контура нефтеносности (т.е. когда Положение границы области пониженного давления оценивают по формуле Э.Б. Чекалюка: Вторая фаза наступает с момента изменения давления на контуре нефтеносности. Теория упругого режима создавалась трудами многих ученых как отечественных, так и иностранных. В их числе:
|
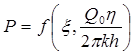
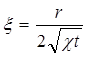
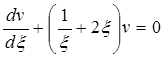
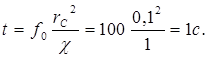
(1)
(2)
до 
1/Па.
до 
1/Па.
(3)
до 
1/Па.
(4)
— коэффициент упругоемкости пласта, 1/Па; Vп – геометрический объем пласта, м 3 ; 
— понижение пластового давления 
.
1/Па, упругий запас — 
м 3 , начальный геологический запас нефти в продуктивном пласте — 
м 3 .
(5)
(6)
(7)
(8)
(9)
— коэффициент, учитывающий объемное расширение жидкости и среды.
— безразмерное время:
(10)
(11)
). При этом её длительность равна:
(12)
(13)
, (14)
;
.
, (15)
, (16)
.
(17)
(18)
,
(19)
;
(20)
получаем
,
— параметр Фурье.
следует пользоваться режимом Ван-Эвердингена и У.Херст и А.Хупера.
,
пользоваться строгой гидродинамической формулой нельзя и следует использовать формулы М.Маскета, А.Хупера, А. Ван-Эвердингена, У.Херста. Так, формула М.Маскета, имеет вид:
(21)
подсчитана А. Ван-Эвердингеном и У.Херстом для значений 
, (22)
— параметр Фурье.
(23)
, (24)
, (25)
, (26)
)
, (27)
(28)
; 
; 
— пространство измерения.
табулирована.
(29)
(30)
(31)
и 
— безразмерные функции дебита и накопленной добычи (табулированы У. Херстом, А. Ван-Эвердингеном).
æ.
, (32)
