Управляемая каноническая форма уравнений состояния

Тема: «Канонические формы уравнений состояния»

Математические модели объектов управления первоначально получаются на основе расчетных данных и физического поведения объекта. В этом случае переменные состояния представляют собой физические переменные объекта, и описания в пространстве состояний объективно связываются с физической реальностью.

В некоторых случаях, однако, полезно ввести переменные состояния, которые формально определяются как линейная комбинация различных физических переменных. Такое преобразование выполняется в целях получения определенных канонических форм уравнений состояния, что облегчает обнаружение некоторых свойств объекта и системы или позволяет описать их с помощью меньшего числа параметров, а также установить для односвязных систем (с одним входом и одним выходом) непосредственную связь векторно-матричных моделей с моделями типа “вход — выход”.

Рассмотрим n-мерный вектор — допустимый вектор состояния некоторой системы и невырожденную матрицу T (n x n). Тогда вектор z=Tx — также возможный вектор состояния рассматриваемой системы.

Реальная система с вектором состояния x описывается следующими уравнениями при D=0:

Эта же система с вектором состояния z:

Подставляя выражение x=T — 1 z в (5.1) , получим

Умножая первое уравнение (5.3) слева на T, получим

Сравнивая (5.4) и (5.2), легко установим, что

Таким образом, матрицы А, В, С зависят от используемого координатного базиса.

Интерес представляют инварианты, полученные после преобразования.

Теорема 5.6. Характеристическое уравнение непрерывной и дискретной систем является инвариантом, если новые состояния вводятся через невырожденную матрицу Т.

Для доказательства теоремы запишем характеристический полином матрицы z A:

Таким образом, характеристическое уравнение матрицы состояния и ее собственное значение не зависят от базиса пространства состояний.

Следовательно, можно утверждать, что свойства систем не изменяются при изменении базиса пространства состояний.

Например, ранг матрицы управляемости не изменяется, так как

или в краткой форме

Ранг матрицы наблюдаемости также не изменится, поскольку

Из (5.8) и (5.10) могут быть получены полезные соотношения для поиска соответствующей матрицы преобразования:

Особый интерес представляют так называемые канонические формы, названные в силу их простоты и непосредственной связи элементов матрицы состояния с коэффициентами характеристического уравнения или для односвязных систем с коэффициентами полиномов передаточной функции.

Каноническая форма управляемости

Здесь и далее остановимся на рассмотрении только односвязных динамических систем.

Предположим, что характеристическое уравнение матрицы А имеет вид

и матрица управляемости не вырождена. Тогда существует такое преобразование, при котором преобразованная система имеет вид

или в компактной форме

Соответствующая передаточная функция системы, описываемой уравнениями состояния (5.13), имеет вид

Матрица преобразования ВММ в каноническую форму управляемости может быть найдена по уравнениям (5.11). Однако этот процесс трудоемкий, поэтому можно использовать другие существующие способы ее определения.

Первый способ основан на использовании так называемой матрицы Фробениуса [14], которая представляет собой матрицу состояния системы в не рассматриваемой здесь канонической форме достижимости, или

— матрица управляемости размером n x n, а₀, а₁. а_n-1 — коэффициенты характеристического уравнения (5.12), которые могут быть найдены в результате расчета матрицы Фробениуса.

Матрица преобразования v T вычисляется с помощью следующего выражения

Таким образом, алгоритм преобразования ВММ к канонической форме управляемости (5.14) включает в себя следующие операции:

1. Вычисление матрицы управляемости Q_у согласно (5.17).

2. Вычисление матрицы Фробениуса F по формуле (5.16), транспонирование F для определения v A=F T .

3. Вычисление матрицы v Q линейного преобразования по формуле (5.18).

4. Вычисление матрицы выхода, определяющей выходную переменную y по новому вектору состояния z:

Второй способ позволяет вычислить матрицу преобразования v Q рекуррентно по столбцам q_i

Действительно, на основании приведенных выше рассуждений можно записать:

Так как вектор v B известен, то мы можем сначала вычислить

и далее продолжить вычисления по отдельным столбцам справа налево:

Последняя строка может служить для контроля.

Коэффициенты a_i, i=0,1,2. n-1, матрицы v А можно определить с помощью определителя .

Пример 5.1. Выполним переход к канонической форме управляемости для непрерывной ВММ электродвигателя постоянного тока.

В пространстве состояния получим

Запишем характеристическое уравнение системы

из которого следует, что матрицы состояния и управления в новом координатном базисе будут иметь следующий вид

Определим матрицу преобразования Q.

Первый способ. Используем выражение (5.18) , которое для нашего примера запишется следующим образом

Такой же результат получается и по второму способу. Из выражения (5.20) получаем

Теперь определим матрицу v C в новом координатном базисе

Таким образом, ВММ нашего объекта в канонической форме управляемости принимает следующий вид

Каноническая форма наблюдаемости

Если желательно иметь матрицу в простейшей форме, то можно воспользоваться так называемой канонической формой наблюдаемости:

или в компактной форме

Как видно из выражений (5.13) и (5.22), матрицы состояний обеих канонических форм идентичны, то есть .

Для канонической формы наблюдаемости матрица наблюдаемости — единичная матрица, то есть

Для нахождения матрицы N B= N TB= N Q -1 B матрица N Т может быть вычислена согласно выражению (5.11):

Так как в нашем случае , получаем, что матрица преобразования ВММ в каноническую форму наблюдаемости (5.22) соответствует матрице наблюдаемости исходной системы

В таком случае выражение для вычисления матрицы N B принимает следующий вид:

Пример 5.2. Выполним переход к канонической форме наблюдаемости для непрерывной ВММ электродвигателя постоянного тока (5.21).

Здесь нам необходимо только определить новое содержание матрицы N B. Для этого воспользуемся выражением (5.26)

Таким образом, ВММ нашего объекта в канонической форме наблюдаемости принимает следующий вид

Основные свойства объектов и систем управления можно оценить в автоматизированном режиме с помощью подсистемы Анализ Компьютерного комплекса функционального проектирования динамических систем (FuncPro 1.0). На рис. 5.1 приведено основное окно подсистемы, в котором раскрыто меню «Анализ»

Рис. 5.1. Основное окно подсистемы «Анализ»

Контрольные вопросы к лекции № 5.

1. Какие свойства и характеристики системы изменятся после преобразования ее векторно-матричной модели к новому координатному базису с помощью невырожденной матрицы Т.

2. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме управляемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

3. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме наблюдаемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

4. Какова будет матрица наблюдаемости непрерывной системы

ОТВЕТЫ

внутреннее содержание матриц состояния А(Ф), управления по состоянию В(Г), выхода С.

матрицы выхода по состоянию

матрицы управления ;

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Электронный учебник по ТАУ (теория автоматического управления)

Видео:Метод пространства состояний САУ: описание конкретной системыСкачать

ТАУ Модели «вход – состояние – выход»

ТАУ предлагает два основных подхода к анализу и синтезу линейных САУ. Первый базируется на структурных схемах и ПФ отдельных элементов и всей системы. В связи с этим его часто называют операторно—структурным. Другой его особенностью является использование физических величин в качестве переменных. Подробно этот подход рассмотрен при изучении ММ типа «вход – выход» (см. п. 2.1).

Второй подход отличается описанием САУ системой ОДУ первого порядка, составленных относительно переменных состояния. Переменные состояния при таком описании САУ аналогичны обобщенным координатам, используемым в теоретической механике. Сам подход к исследованию САУ получил название метода пространства состояний или метода переменных состояния.

Понятие пространства состояний

Согласно методу пространства состояний (МПС) все переменные величины, характеризующие САУ, разделяют на три группы:

1) входные переменные или входные (управляющие) воздействия u m ;

2) выходные переменные y p , характеризующие реакцию САУ на входные воздействия;

3) переменные (координаты) состояния x n , характеризующие динамическое поведение САУ.

Взаимосвязь названных переменных поясняют схемой САУ, на которой систему изображают в виде «черного ящика» в соответствии с рисунком 2.29.

Отдельные части САУ характеризуют ПФ W 1 (s) и W 2 (s). Как следует из схемы, переменные состояния x n являются промежуточными величинами. Их относят к содержимому «черного ящика». Следовательно, они скрыты от прямого наблюдения. Кроме того, переменные состояния

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

y 2 ( t )

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

u 1 ( t )

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

u 2 ( t )

Видео:c15 1, Пространство состояний: представлениеСкачать

u m ( t )

Видео:11. Прямая в пространстве и ее уравненияСкачать

x 1 ( t )

Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

x 2 ( t )

Видео:определение коэффициентов и свободных членов канонических уравнений. Решение канонического уравненияСкачать

x n ( t )

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

y 1 ( t )

Видео:Халилов В. Р. - Теоретическая механика - Канонические уравнения (Лекция 4)Скачать

y n ( t )

Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

W 1 ( s )

Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

W 2 ( s )

не всегда являются физическими величинами. Иногда для удоб­ства математического моделиро­вания САУ целенаправленно отказываются от физического содержания переменных состоя­ния. Поэтому в общем случае x n (t) являются абстрактными переменными. Однако они должны однозначно выражаться через физические величины y p (t).

В общем случае исследуемую САУ считают многомерной (рисунок 2.29). Для упрощения работы с многомерными величинами их представляют в векторно-матричном виде. Так, совокупность входных переменных представляют в виде вектора входа совокупность выходных переменных – в виде вектора выхода а совокупность переменных состояния – в виде вектора состояния

Согласно МПС множество всех значений, которые может принять вектор входа U в момент времени t, образует пространство входа исследуемой САУ. Аналогично, множество всех значений, которые может принять вектор выхода Y в момент времени t, образует пространство выхода, а множество всех значений, которые может принять вектор состояния X в момент времени t, образует пространство состояний САУ.

Как было отмечено, векторно-матричные уравнения (2.82) описывают многомерную САУ. Эта же совокупность уравнений служит ММ одномерной САУ, т.е. системы с одним входом и одним выходом. При использовании МПС такие САУ часто называют системами со скалярным входом и выходом, так как входная и выходная величины являются скалярными. Уравнения состояния и выхода одномерной системы имеют вид

Видео:A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать

Канонические формы уравнений состояния

Разработано множество эквивалентных форм (представлений) уравнений состояния, различающихся между собой видом матриц A , B и C . Одни из форм используются чаще, так как обладают в некоторых случаях известными преимуществами перед другими. Такие формы записи уравнений состояния называются каноническими. Считают, что удобство канонических форм заключается в следующем. Во-первых, канонические представления матриц обеспечивают минимальное количество ненулевых элементов, что заметно упрощает вычисления. Во-вторых, канонические представления приводят к простым алгоритмам синтеза оптимальных регуляторов замкнутых САУ /3/.

Таким образом, в результате приведения уравнений к канонической форме более простую структуру принимают две из трех матриц: A и B (управляемые формы) или A и C (наблюдаемые формы). Управляемые канонические формы используют при синтезе регулятора, а наблюдаемые канонические формы – при синтезе наблюдателя /23/.

Первая управляемая каноническая форма

Первой управляемой канонической формой называют специальные матрицы

Очевидно, что коэффициенты характеристического полинома A(s) составляют последний столбец матрицы A. Матрицы такого вида называют матрицами Фробениуса. Элементы таких матриц определяют без вычислений. Характеристический многочлен A(s) совпадает со знаменателем ПФ системы управления. Корни данного многочлена определяют устойчивость и качество переходных процессов в САУ.

Матрица входа B рассматриваемого канонического представления также имеет специальный вид. Вследствие скалярного входного воздействия матрица B представляет собой вектор-столбец, элементы которого также не требуется вычислять.

Полученная ММ системы управления может быть изображена в виде структурной схемы, представленной на рисунке 2.31.

Принятые переменные состояния являются выходными сигналами интеграторов.

Первую управляемую каноническую форму называют также канонической формой дуальной фазовой переменной /20/.

Видео:Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать

Лекция 4. Цель введения новых переменных состояния – получение более простой формы матриц А, В, С, а следовательно и уравнений системы.

Цель введения новых переменных состояния 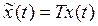– получение более простой формы матриц А, В, С, а следовательно и уравнений системы.

Из различных канонических форм в данном курсе будут использоваться управляемая каноническая форма, которую называют также просто управляемой формой, и наблюдаемая каноническая форма.

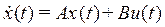
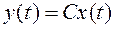
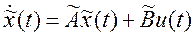
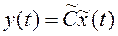
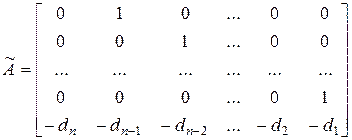
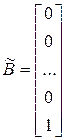
Пусть система с одним входом и одним выходом описывается уравнениями (1) , . Тогда путем соответствующего выбора матрицы Т эти уравнения можно привести к управляемой канонической форме, имеющей вид уравнений (3) , при

, .

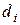
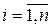
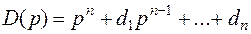
Здесь , , являются коэффициентами характеристического многочлена системы

.

Преимущество управляемой формы заключается в простоте вычислений передаточной функции и закона управления с обратной связью по состоянию (см. ниже).

Для систем с одним входом и одним выходом к каноническим формам уравнений в переменных состояния можно придти другим путем, не прибегая к помощи матрицы T, а именно используя передаточную функцию системы. Передаточная функция системы с одним входом и одним выходом имеет вид

.

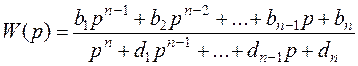
При этом уравнения в переменных состояния, как показано, могут быть представлены в следующих канонических формах:

1. Управляемая каноническая форма:

, .

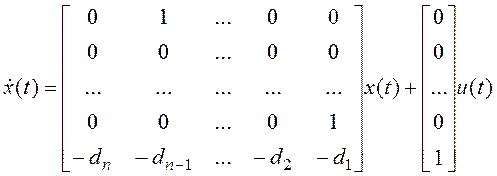
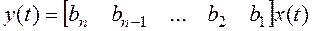
2. Наблюдаемая каноническая форма:

, .

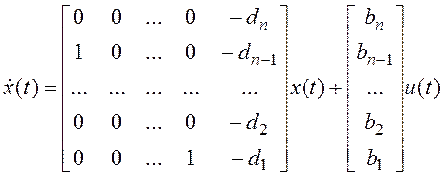
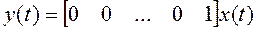
Такое преобразование применимо к ПФ, описывающей минимальную реализацию (представление) математической модели системы, которую (реализацию) можно найти путем сокращения всех одинаковых сомножителей в числителе и знаменателе исходной ПФ. Уравнения в переменных состояния, соответствующие ПФ 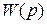системы, называют реализацией системы.

Минимальная реализация определяется как математическая модель самого низкого порядка из множества моделей, обеспечивающих то же самое преобразование «вход-выход». Возможность перехода к каноническим формам уравнений в переменных состояния тесно связана со свойствами управляемости и наблюдаемости системы.

Дата добавления: 2015-08-14 ; просмотров: 1400 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

🎬 Видео

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

c16 1, Управляемость и наблюдаемость: управляемость, определение и критерийСкачать

Коэффициенты и свободные члены канонических уравнений метода перемещенийСкачать

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать