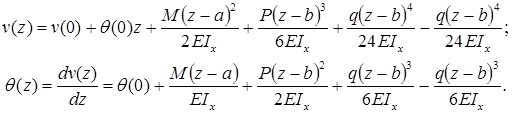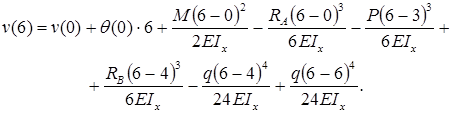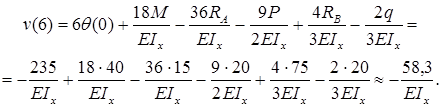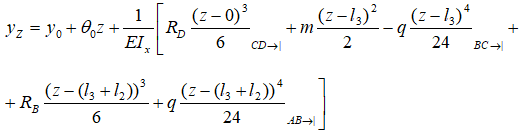Универсальное уравнение для изогнутой оси балки

Видео:Построение эпюры прогибов балкиСкачать

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

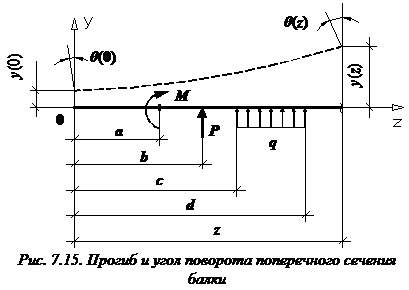
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 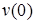и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

Уравнение упругой линии балки на примере

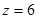
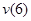
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .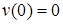

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

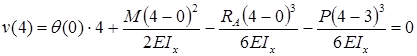
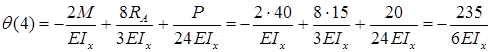
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

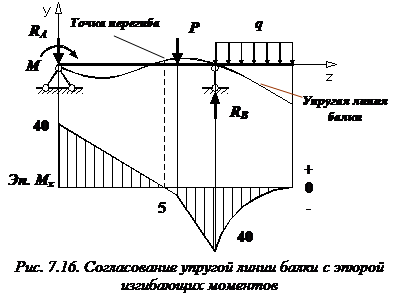
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Универсальное уравнение оси изогнутого бруса (метод начальных параметров)

Видео:Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать

Универсальное уравнение оси изогнутого бруса (метод начальных параметров)

• Универсальное уравнение для криволинейной оси Балки(метод начальных параметров) Задача определения прогиба решается путем применения так называемого универсального уравнения оси криволинейной балки, или, как часто говорят, вывода универсального уравнения упругой линии, основанного на так называемом методе начального параметра, который широко используется в строительной механике. Таким образом 279прогиб любого сечения балки определяется коэффициентами смещения и силы, принятыми в начале координат, с учетом нагрузки,

приложенной к балке. Представим себе, что на балку действует любая система нагрузок. 248, а. Интенсивность нагрузки и концентрированный ТАТ при этом совпадают с направлением оси ОП, которая направлена вверх. Внешний сосредоточенный момент положителен при действии по часовой стрелке. Начало координат совместимо с центроидом секции в дальнем левом углу луча. Жесткость балки считается определенной длиной. Для каждой секции разделите несколько секций за один раз так, чтобы изгибающий момент был представлен непрерывной функцией

Сила давайте щи-положительная, что направление Все ее балки на полу на растяжке — Людмила Фирмаль

— о- • • Граничная точка/, 2,… Кроме того, разделительная секция должна быть размещена в тех секциях, где происходит изменение закона балансировки нагрузки. Так, например, происходит переход к закону нагрузки a Людмила Фирмаль

(9.6). В этом решении вместо координаты x нам нужно взять координаты, которые отсчитываются от точки 7, а именно (x-P1). Вместо значения M o -,

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Изгиб Л.4 \ ДУ изогнутой оси (метод Коши-Крылова)Скачать

iSopromat.ru

Метод начальных параметров (сокр. — МНП) позволяет определять прогибы и углы наклона сечений в прямых балках с постоянной жесткостью поперечного сечения EI_x.

МНП является одним из относительно простых способов расчета угловых и линейных перемещений при изгибе в балках с любым количеством силовых участков.

Пример расчета перемещений сечений балки смотрите в нашем видеоуроке:

Для применения метода начальных параметров есть ограничения: рассчитываемая балка должна быть выполнена из однородного материала, иметь прямую ось и постоянные форму и размеры поперечного сечения.

Видео:Метод начальных параметров ( МНП ). СопроматСкачать

Универсальные уравнения МНП

Для балок с типичным набором нагрузок универсальные уравнения метода начальных параметров имеют вид: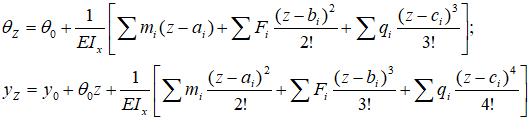

где
θ_z, y_z – соответственно угловое и линейное перемещения рассматриваемого сечения балки;
θ₀, y₀ – угол наклона и прогиб сечения балки в выбранном начале координат (НК). Это и есть начальные параметры (являются постоянными интегрирования) по которым назван сам метод. Определяются из соответствующих опорных условий;
m, F и q – все сосредоточенные моменты (пары сил), силы (включая опорные реакции) и распределенные нагрузки (в т.ч. компенсирующие) приложенные к рассматриваемой балке;
z – расстояние от выбранного начала координат до рассматриваемого сечения балки (положение сечения);
a и b – расстояния от начала координат до соответствующих моментов и сосредоточенных сил;
c – расстояние от НК до начала действия распределенной нагрузки;
E – модуль продольной упругости материала балки;
I_x — момент инерции сечения относительно оси x.

Данные уравнения МНП являются лишь шаблонами, по которым записываются уравнения для конкретных расчетных схем (пример рассмотрен ниже).

Видео:Прогиб консоли (2). Уравнение осиСкачать

Примечания к методу

Перед записью уравнений метода начальных параметров выбирается начало координат балки.

Начало координат выбирается в крайнем левом или правом конце балки (лучше в том, который расположен на опоре).

Слагаемые в уравнениях записываются последовательно по силовым участкам от начала координат.

Знаки отдельных слагаемых в универсальных уравнениях МНП принимаются по правилу знаков для изгибающего момента, т.е. слагаемые с нагрузками, которые на рассматриваемом участке стремятся сжать верхние слои балки, записываются положительными.

Если распределенная нагрузка q действует в пределах части длины балки (обрывается, не доходя до конца), то ее действие продлевается в сторону, противоположную от начала координат, до конца балки и добавляется компенсирующая нагрузка той же интенсивности но обратного направления.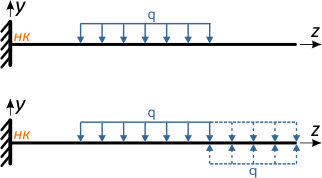

Начальные параметры универсальных уравнений МНП определяются из условий закрепления балки в опорах.
На шарнирных опорах вертикальные линейные перемещения (прогибы) равны нулю, т.е. y_A=0 и y_B=0.

В жесткой заделке отсутствуют (равны нулю) и угловые и линейные перемещения (θ_A=0, y_A=0).

Положительное значение рассчитанного прогиба y_z соответствует перемещениям сечения вверх по отношению к продольной оси балки.

Знак угла поворота θ_z зависит от выбора начала координат: при выборе НК в крайнем левом сечении балки угол θ_z будет считаться положительным при повороте сечения против хода часовой стрелки

Соответственно, если начало координат выбрано справа – положительным считается угол при повороте по часовой стрелке.

Видео:14. Интеграл мора ( практический курс по сопромату )Скачать

Пример составления уравнений МНП

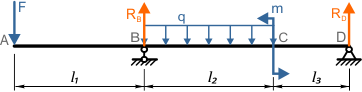
Порядок составления уравнений МНП и расчета перемещений рассмотрим на примере двухопорной балки

Выбор начала координат

Начало координат в данной расчетной схеме выбираем в самой правой точке D балки, так как она расположена на опоре, и, следовательно, прогиб в этой точке будет отсутствовать.
Ось z направляем соответственно влево.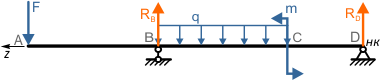

Теперь для данной балки правый торец будем считать ее началом, левый – соответственно концом.

Действия с распределенной нагрузкой

Как видно по схеме, действие распределенной нагрузки обрывается в точке B, не доходя до конца балки.

Поэтому ее действие необходимо продлить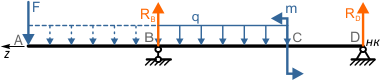

при этом схема нагружения балки изменилась. Теперь, чтобы вернуться к начальной системе нагрузок, добавляем компенсирующую распределенную нагрузку обратного направления.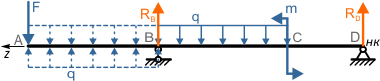

Это действие выполняется, потому что в уравнениях МНП параметр «c» учитывает только начало действия нагрузки.

Составление уравнений МНП

Универсальные уравнения МНП для заданной балки записываются последовательно по участкам со стороны начала координат.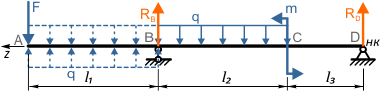

При этом желательно отделять части уравнения для каждого из участков.

Запишем уравнение угловых перемещений θ_z метода начальных параметров.
Участок CD
Мысленно закрепив балку между сечениями C и D,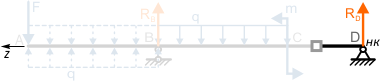

в стороне начала балки видим только опорную реакцию R_D которая по правилу знаков записывается положительной, так как сжимает верхние слои балки.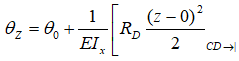

Участок BC
На этом участке, как и на всех остальных, закрепив балку в произвольном месте, смотрим в сторону НК.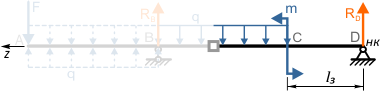

Видим момент m и распределенную нагрузку q.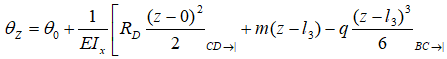

Момент положителен т.к. сжимает верхние слои балки, нагрузка q отрицательна т.к. сжимает ее нижние слои.

Заметим, что здесь мы записали сразу всю «верхнюю» распределенную нагрузку q. В данном уравнении для других участков ее записывать больше не надо.
Участок AB
При рассмотрении данного участка к уравнению добавляются реакция в опоре B и «нижняя» компенсирующая нагрузка q.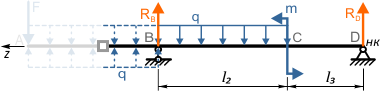

Записываем их положительными, т.к. они стремятся сжать верхние слои балки.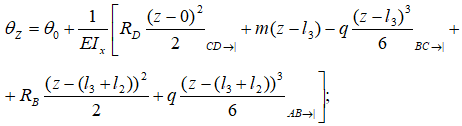

Силы и моменты, приложенные в самом конце балки, в уравнения не входят.
На вопрос «Разве сила F не влияет на перемещение сечений?» ответ следующий: В уравнениях метода начальных параметров поперечная сила и момент, приложенные к концу балки оказывают влияние на перемещения опосредованно, через опорные реакции R.

Уравнение метода начальных параметров для прогибов составляется аналогично.

Определение начальных параметров

В правой части полученных уравнений известны все параметры кроме начальных θ₀ и y₀ (переменная z задается при решении).

Прогиб и угол наклона сечения в начале координат определим из опорных условий.

Балка закреплена на двух шарнирных опорах (точки B и D), в которых прогибы всегда равны нулю.

Граничные условия метода начальных параметров: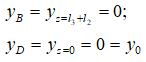

Так как точка D была принята за начало координат, то прогиб в этой точке и есть y₀, т.е. правильно выбрав НК, мы сразу определили один из двух начальных параметров.

Угловое перемещение в начале координат θ₀ рассчитаем из оставшегося (первого) опорного условия.

Для этого запишем уравнение прогибов для точки B, которое равно нулю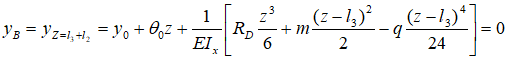

От НК до сечения B два участка, поэтому берется не все уравнение, а только его части, включающие нагрузки на соответствующих участках (CD и BC).
Из него выражаем и находим значение θ₀.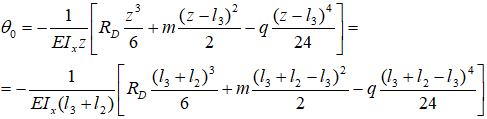

Теперь можно рассчитывать перемещения любого сечения балки.

Расчет перемещений

Для определения перемещений сечения расположенного на i-м участке от начала координат в расчете участвуют только части уравнений от НК до i-го участка включительно.

Выбирая нужное уравнение и задавая положение z сечений от начала координат определяются их угловые и линейные перемещения.

Например, для расчета угла наклона и прогиба сечения K расположенного на расстоянии z_K от НК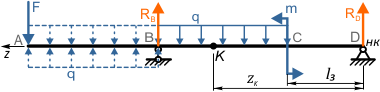

уравнения метода начальных параметров будут иметь вид: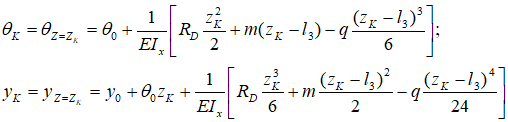

Остается только подставить значения и провести расчеты.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

💥 Видео

Двутавровые балки без станков своими руками!!!Скачать

Делаю лаги перекрытия из OSB своими руками. I make overlapping logs from OSB with my own hands.Скачать

Метод начальных параметров Расчет перемещений сечений балкиСкачать

Диф уравнение изогнутой оси балкиСкачать

Прогиб балки путем интегрирования диф уравненияСкачать

Дифференциальные уравнения и прогиб балкиСкачать

Перемещения при изгибе. Общие понятия. Вывод ур-я изогнутой оси в форме метода нач. параметров.Скачать

13. Метод начальных параметров ( практический курс по сопромату )Скачать

Дифференциальные уравнения при поперечном изгибе. ПРАВИЛЬНЫЙ СОПРОМАТ. Видео 1 Часть 1.Скачать

Перемещения при изгибе. Часть 2. Непосредственное интегрирование уравнения изогнутой осиСкачать

Изгиб С.3: расчёт на прочность и жёсткостьСкачать