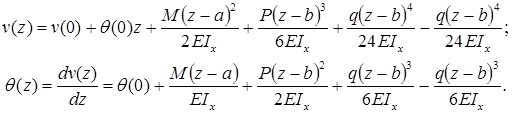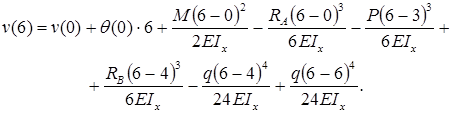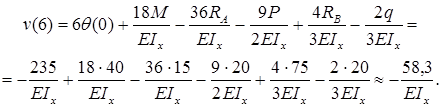Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
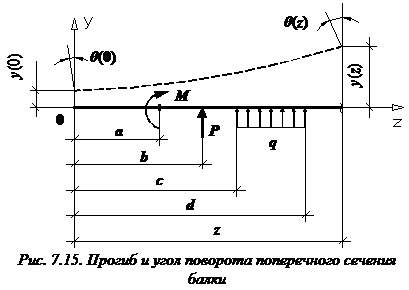
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб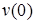 
и угол поворота 
балки в начале координат (начальные параметры) определяются из условий закрепления балки.
Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать
Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при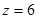 
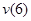
м, то есть 
. Запишем универсальное уравнение упругой линии балки :
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: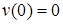 
.
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
,
.
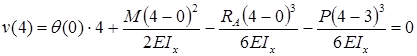
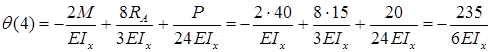
Прогиб консоли при z=6м:
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
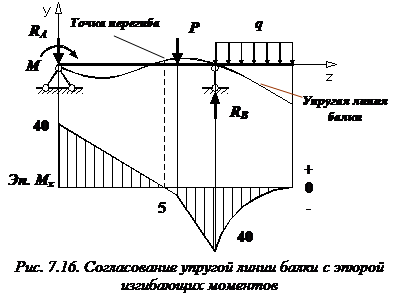
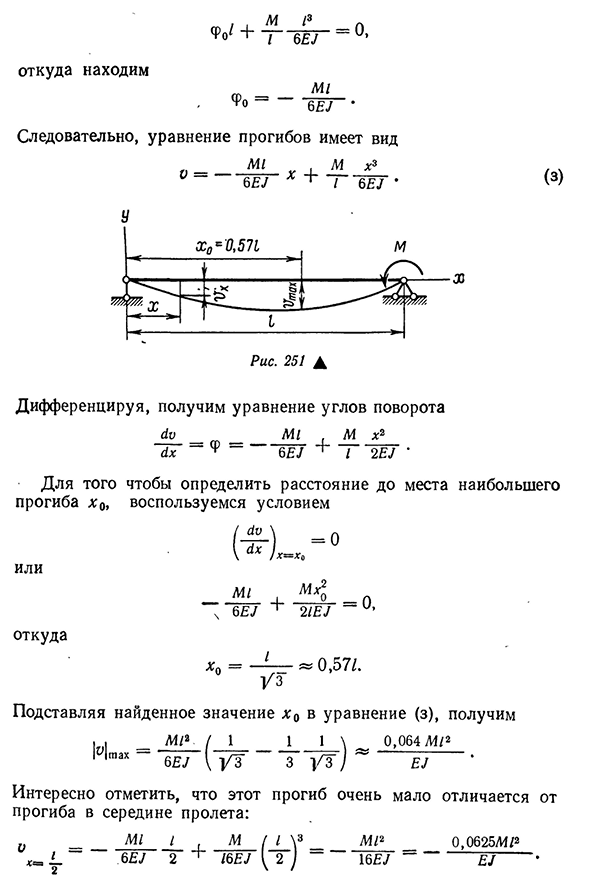
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Видео:Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать
Изогнутая ось балки
Изогнутая ось балки
Изгиб балки сопровождается искривлением ее оси. При этом точки оси получают поперечные перемещения или прогибы, а поперечные сечения поворачиваются относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона j касательной к изогнутой оси балки. Прогибы и углы поворота в балках часто называются линейными и угловыми перемещениями.
 |
— закон изменения прогиба оси балки;
АМВ – изогнутая ось (упругая линия) – кривая, в которую превращается прямолинейная до деформации ось балки после приложения нагрузки;
— угол наклона касательной.
Прогибы и углы поворота в балках являются переменными величинами, т. е. функциями координаты х.
О знаке :
j — положительно, если при совмещении оси балки с касательной идет движение по часовой стрелке.
 |
На часть конструкций часто накладываются жесткие ограничения на перемещения, например для балочных мостов, кран-балок и т. д., т. е. возникает необходимость рассмотрения геометрической стороны задачи при изгибе.
I . Дифференциальное уравнение изогнутой оси балки
Вид ИОБ определяется
1. действием нагрузки, которая вызывает внутренние усилия M , Q , N ;
2. геометрической характеристикой I ;
Значит 
I – момент инерции поперечного сечения балки относительно его нейтральной оси;
Е – модуль упругости материала балки.
, E , I – от x не зависят.
В лекции «Напряжения в случае плоского поперечного изгиба балки» (прошлый семестр) рассматривалось «Определение нормальных напряжений». При этом было рассмотрено 3 стороны задачи:
1. геометрическая сторона задачи;
2. физическая сторона задачи;
3. статическая сторона задачи.
При рассмотрении геометрической стороны задачи была установлена зависимость
, где
— относительная деформация;
— прогиб оси балки;
— радиус кривизны ИОБ.
При рассмотрении физической стороны задачи была использована гипотеза о том, что продольные волокна балки не давят друг на друга, т. е. что изгиб сводится к деформациям продольных волокон, которые деформируются изолированно, испытывая простое одноосное растяжение (сжатие). Эта гипотеза делает возможным для связи деформаций и напряжений при изгибе использование закона Гука.
В статической стороне задачи было рассмотрено следующее сечение
Суммарное действие внутренних напряжений должно быть равно внешним воздействиям.
Имеет место 2 условия равновесия:
1. 
2. 
— сила по элементарным площадкам;
— сила по всему сечению.
Отсюда 
(1),
— радиус кривизны ИОБ;
— жесткость балки при изгибе (изгибная жесткость).
Так как в выражение (1) вошли все 3 фактора M , E , I , то осталось выразить 
через y .
Для этого воспользуемся выражением из высшей математики
(2)
Приравниваем (1) и (2).
(3) точное дифференц. уравнение ИОБ
Так как в реальных конструкциях нормами проектирования допускаются сравнительно малые прогибы, а именно
, то ИОБ в реальности пологая.
Угол 
Поскольку 
, а 
, то этим слагаемым в выражении (3) можно пренебречь.
(4)
Эта формула устанавливает зависимость между 
,и 2-ой производной 
от прогиба.
Известно, что 
, когда момент, растягивая нижние волокна, обращает балку выпуклостью вниз.
Тогда из математики 
(вторая производная от функции отрицательна, если кривая обращена выпуклостью в положительную сторону оси y ).
 |
Таким образом, при положительном изгибающем моменте, 2-ая производная должна быть отрицательной, следовательно в уравнении (4) удерживается знак «-» и формула имеет вид
(5) приближенное дифференц. уравнение ИОБ
Основные дифференциальные зависимости
Ранее известные зависимости:
(6)
, 
(7)
Уравнения (7) позволяют, имея q , Q и M (а эти величины всегда возможно определить, построив эпюры в балках), получить значения y (прогиба) и j (угла поворота).
II . Методы решения дифференциальных уравнений ИОБ
Существует 3 метода решения дифференциальных уравнений ИОБ:
1. Метод непосредственного интегрирования
2. Метод начальных параметров
1. Метод непосредственного интегрирования
Метод непосредственного интегрирования заключается в непосредственном интегрировании уравнения (5).
(8)
Зная закон изменения можно определить y как функцию от x ().
Интегрирование ведется по участкам, для которых должны быть известны аналитические выражения изгибающих моментов .
В результате двукратного интегрирования на каждом участке появляются 2 произвольные постоянные С1 и С2.
Если балка разбивается на n участков, то постоянных интегрирования будет 2 × n .
Их определяют из
1. граничных условий (способов закрепления);
2. условий сопряжения участков.
1. Условия закрепления (граничные условия)
1) жесткое защемление
При 
Þ 
и 
2) шарнирное опирание
При Þ и 
При 
Þ и
Таким образом, с учетом граничных условий осталось 
неизвестных.
2. Условия сопряжения граничных участков
при 
Þ 
, 
Таким образом, всегда можно составить условия сопряжения и найти уравнение ИОБ.
Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать
Универсальное уравнение оси изогнутого бруса (метод начальных параметров)
Видео:Прогиб консоли (2). Уравнение осиСкачать
Универсальное уравнение оси изогнутого бруса (метод начальных параметров)
- Универсальное уравнение для криволинейной оси Балки(метод начальных параметров) Задача определения прогиба решается путем применения так называемого универсального уравнения оси криволинейной балки, или, как часто говорят, вывода универсального уравнения упругой линии, основанного на так называемом методе начального параметра, который широко используется в строительной механике. Таким образом 279прогиб любого сечения балки определяется коэффициентами смещения и силы, принятыми в начале координат, с учетом нагрузки,
приложенной к балке. Представим себе, что на балку действует любая система нагрузок. 248, а. Интенсивность нагрузки и концентрированный ТАТ при этом совпадают с направлением оси ОП, которая направлена вверх. Внешний сосредоточенный момент положителен при действии по часовой стрелке. Начало координат совместимо с центроидом секции в дальнем левом углу луча. Жесткость балки считается определенной длиной. Для каждой секции разделите несколько секций за один раз так, чтобы изгибающий момент был представлен непрерывной функцией
Сила давайте щи-положительная, что направление Все ее балки на полу на растяжке — Людмила Фирмаль
— о- • • Граничная точка/, 2,… Кроме того, разделительная секция должна быть размещена в тех секциях, где происходит изменение закона балансировки нагрузки. Так, например, происходит переход к закону нагрузки a Людмила Фирмаль
(9.6). В этом решении вместо координаты x нам нужно взять координаты, которые отсчитываются от точки 7, а именно (x-P1). Вместо значения M o -,
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎦 Видео
Метод начальных параметров ( МНП ). СопроматСкачать
Построение эпюры прогибов балкиСкачать
Изгиб Л.4 \ ДУ изогнутой оси (метод Коши-Крылова)Скачать
Дифференциальные уравнения и прогиб балкиСкачать
Дифференциальные уравнения при поперечном изгибе. ПРАВИЛЬНЫЙ СОПРОМАТ. Видео 1 Часть 1.Скачать
Диф уравнение изогнутой оси балкиСкачать
Перемещения при изгибе. Часть 2. Непосредственное интегрирование уравнения изогнутой осиСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
Прогиб балки путем интегрирования диф уравненияСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
11. Уравнения в полных дифференциалахСкачать
12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать
Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать
