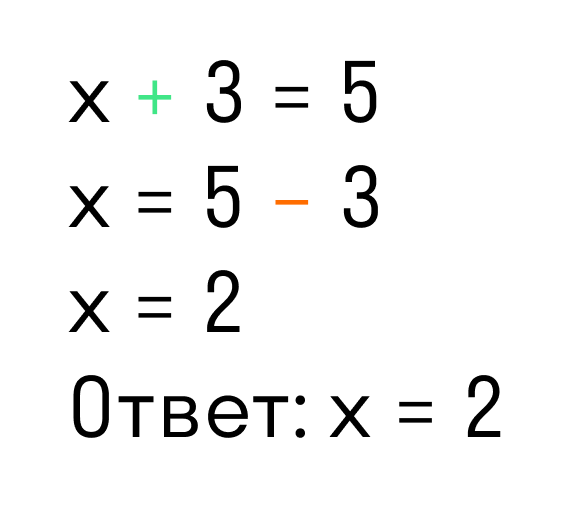Умножение и деление обеих частей уравнения на одно и тоже число

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.
• Одночлены, из которых состоит многочлен, называют членами многочлена.
• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

• все решения уравнения являются координатами точек, принадлежащих графику;
• координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Видео:Как умножать или делить обе части уравнения на одно и тоже число.Скачать

Математика. 6 класс

Конспект урока

Перечень рассматриваемых вопросов:

Уравнение – равенство содержащее букву, значение которой надо найти.

Решить уравнение – значит найти все его корни.

Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Как решаются уравнения? Чем уравнение отличается от буквенного выражения? На эти и другие вопросы, связанные с уравнениями, мы сегодня и будем отвечать.

Дадим определение уравнению. Уравнением называют равенство, содержащее букву, значение которой надо найти.

Например, 2х – 5=17.

Решить уравнение – значит найти все его корни.

В нашем случае x=11.

Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.

Подставим в уравнение корень

Получается, что левая и правая части равны семнадцати.

При решении уравнений можно использовать следующие приёмы:

– переносить числа из одной части уравнения в другую, меняя их знак на противоположный.

– делить или умножать обе части уравнения на одно и тоже число отличное от нуля.

Равенство не изменится, если к обеим частям уравнения прибавить по числу три икс:

Перенесём число 7 из левой части в правую часть уравнения с противоположным знаком:

Применим распределительный закон для правой части:

Упростим левую и правую части уравнения:

Равенство не изменится, если обе части уравнения разделить на 5:

2 ∙ (– 3) + 7 = – 3 ∙ (– 3) – 8,

Значит, корень уравнения найден верно.

Перенесём число 3 в правую часть уравнения с противоположным знаком:

Где используются уравнения?

Ответ на этот вопрос достаточно прост. Уравнения используются практически везде. В школе мы решаем с помощью уравнений текстовые задачи. В окружающем нас мире все природные и жизненные процессы протекают по определённым закономерностям, большинство из которых можно описать с помощью уравнений. Например, если нужно определить во сколько должен выехать автомобиль, чтобы прибыть вовремя из пункта А в пункт В, необходимо использовать уравнения движения. Для точного расчёта затрат и прибыли на предприятиях используют экономические уравнения. В медицине для обработки данных ультразвуковых исследований организма тоже используются уравнения.

Итак, уравнения – это универсальный инструмент для решения самых разных прикладных задач.

Разбор заданий тренировочного модуля

Тип 1.Найдите корни уравнения.

Перенесём – 5 в правую часть уравнения с противоположным знаком:

Вычислим отдельно левую и правую части уравнения.

Это и есть корень уравнения.

Тип 2. Будет ли являться корнем данного уравнения число 7?

Чтобы выполнить данное задание нужно подставить число 7 вместо неизвестного х и проверить, будут лиравны правая и левая части уравнения. Если будут равны, то число является корнем уравнения, если правая и левая части уравнения не равны, то число не является корнем уравнения.

Видно, что при подстановке в уравнение числа 7 верное равенство не получилось. Следовательно, число 7не является корнем уравнения.

Видео:Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать

Решение простых линейных уравнений

О чем эта статья:

Видео:Теория. Умножение и деление обеих частей уравнения (5-8 класс)Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Решение уравнений, 6 классСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Математика 3 класс (Урок№45 - Уравнения на основе связи между результатами и компонентами "." и ":")Скачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

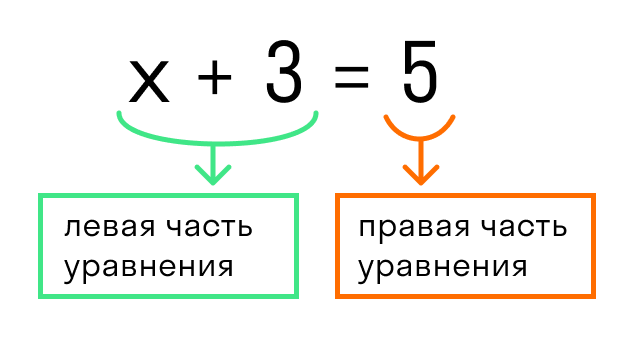
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

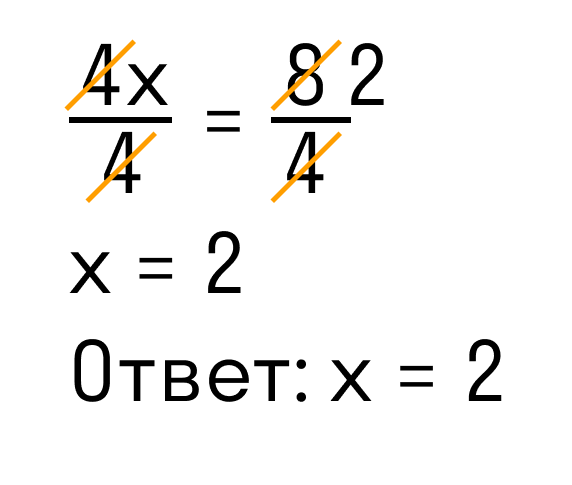
Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Решение уравнений на умножение и деление.Скачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

🎦 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение уравнений.Скачать

Уравнение 5-й степени😱 Все проще, чем кажется🔥Скачать

Линейное уравнение и его разновидности. Алгебра 7 класс.Скачать

Вся суть уравнений за 1 секунду. Хватит путать знаки в уравнениях!Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Уравнение на умножение и деление в одно действиеСкачать

Решение уравнений (относительно умножения и деления). 5 классСкачать

Как решают уравнения в России и США!?Скачать

Как решают уравнения в России и СШАСкачать

Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Математика 2 класс. «Уравнения на умножение и деление»Скачать

Решение уравнений с дробными числами в 6 классеСкачать

Умножение, деление и сложение дробей #математика #алгебра #дроби #5классСкачать