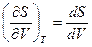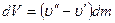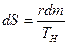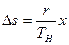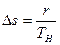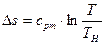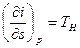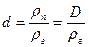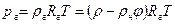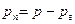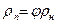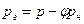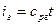Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Ваш ответ
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

решение вопроса
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Похожие вопросы
- Все категории
- экономические 43,424
- гуманитарные 33,634
- юридические 17,906
- школьный раздел 608,194
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнения состояния реальных газов
Реальные газы отличаются от идеальных тем, что их молекулы имеют конечные собственные объемы и связаны между собой силами взаимодействия, имеющими электромагнитную и квантовую природу. С увеличением расстояния между молекулами силы взаимодействия уменьшаются. При уменьшении расстояния между ними силы взаимодействия переходят в силы отталкивания, достигающие очень больших значений.
Таким образом, свойства реальных газов как в количественном, так и качественном отношениях значительно отличаются от свойств идеальных газов. Поэтому все результаты для реальных газов, полученные на основании законов для идеальных газов, будут приближенными и справедливыми лишь при очень больших разрежениях. В связи с этим возникла необходимость в разработке уравнения состояния, которое точно описывало бы состояние реального газа. Одно из таких уравнений было получено Боголюбовым и Ф. Майером:
где Bj — вириальные коэффициенты, выражающиеся через потенциальную энергию взаимодействия данного газа и его температуру.
Однако полученное уравнение в общем виде не может быть использовано для непосредственных расчетов реальных газов ввиду сложностей определения коэффициентов Bj. В отдельных частных случаях, когда известен закон изменения потенциальной энергии взаимодействия между двумя молекулами, в зависимости от расстояния между ними и при наличии определенного количества экспериментальных данных может быть получено расчетное уравнение какого-либо реального газа в достаточно широком диапазоне изменения параметров. Из-за сложности определения вириаль- ных коэффициентов обычно ограничиваются расчетом первых двух из них. В этом случае расчетное уравнение имеет вид
где Л и В — первый и второй вириальные коэффициенты, являющиеся функцией только температуры.
В настоящее время уравнения подобного вида получили широкое распространение при расчете свойств многих реальных газов. Наиболее простым и качественно верно отображающим изменение состояния реального газа является уравнение Ван-дер-Ваальса, которое является частным случаем общего уравнения состояния Майера—Боголюбова, если пренебречь в правой части всеми членами, содержащими 1/и во второй степени и выше. Уравнение Ван-дер-Ваальса было получено в 1873 г. и имеет вид
где b — наименьший объем, до которого можно сжать реальный газ.
Для каждого газа величина b имеет определенное числовое значение; а — коэффициент пропорциональности, имеющий определенное числовое значение для каждого отдельного газа, не зависящее от параметров состояния.
Уравнение Ван-дер-Ваальса качественно верно отражает состояние реальных веществ в жидком и газообразном состоянии. Для двухфазных состояний оно неприменимо. Для одного моля газа уравнение Ван-дер-Ваальса записывается в виде
Если в уравнении Ван-дер-Ваальса раскрыть скобки и расположить полученные величины по убывающим степеням v, то получим уравнение третьей степени относительно удельного объема газа
Из математики известно, что такое уравнение при заданных значениях р и Т должно иметь три корня. При этом возможны следующие три случая:
- • все три корня различны и действительны;
- • все три корня действительны и равны между собой;
- • один корень действительный и два мнимых (комплексных).
В последнем случае реальное значение имеет лишь один действительный корень, так как мнимые корни не имеют физического смысла.
Если на ра-диаграмме построить изотермы, соответствующие уравнению Ван-дер-Ваальса, то они будут иметь вид кривых, изображенных на рис. 1.3, а. Анализ этих кривых позволяет заключить, что при сравнительно низких температурах они имеют в средней части волнообразный характер с максимумом и минимумом. При этом чем выше температура, тем короче волнообразная часть изотермы. Изобара АВ, пересекающая изотерму, дает три действительных значения объема в точках A, D и В (три различных действительных корня).
Наибольший корень, равный удельному объему в точке В, относится к парообразному (газообразному) состоянию вещества, а наименьший (в точке А) — к жидкому состоянию. Участок кривой между точками А и В не имеет физического смысла, так как уравнение Ван-дер-Ваальса неверно описывает состояние двухфазных систем.
Действительный процесс перехода из жидкого состояния в газообразное изображается прямой линией (изобарой) АВ. При этом точка А соответствует состоянию кипящей жидкости, а точка В — состоянию сухого насыщенного пара.
При некоторой температуре, называемой критической, изотерма не будет иметь волнообразного участка. На этой изотерме есть лишь точка пере
а — изотермы, найденные по уравнению Ван-дер-Ваальса; 6 — МК — кривая кипящей
жидкости; NK — кривая сухого пара гиба, касательная к которой должна быть горизонтальной. Это соответствует второму случаю решения уравнения Ван-дер-Ваальса, когда все три корня действительные и равны между собой (точка К на рис. 1.3, а, 1.3, б).
При температурах выше критической изотермы будут иметь монотонно спадающий характер. Здесь будем иметь один действительный корень. Если соединить точки А, Аи А2 и т.д., то получим кривую, на которой жидкость находится в состоянии кипения (пограничная кривая жидкости — кривая А К). Кривая ВК называется пограничной кривой пара. Таким образом, для реального вещества pv-диаграмма условно разбивается на три характерные области.
- 1. Область жидкого состояния, расположенная левее кривой АК.
- 2. Область двухфазного состояния (влажного пара), расположенная между кривыми АК и ВК.
- 3. Область перегретого пара, расположенная правее кривой ВК и выше точки К.
Условно область жидкости ограничивают сверху линией СК, представляющей собой критическую изобару.
Критическое состояние вещества впервые было открыто Д. И. Менделеевым в 1861 г. Критическую температуру он назвал абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю и исчезает различие между жидким и парообразным состояниями вещества. До открытия критического состояния вещества многие газы безуспешно пытались превращать в жидкость одним только увеличением давления. Однако, как это следует из рис. 1.3, б, при температурах, выше критических, жидкое состояние вещества отсутствует. Поэтому для превращения газа в жидкость путем увеличения давления необходимо этот газ охладить до температуры, ниже критической. Только после этого сжатием по изотерме любой газ можно превратить в жидкость.
При больших плотностях уравнение Ван-дер-Ваальса дает значительные ошибки, связанные с тем, что при его выводе не учитывались явления силовой ассоциации и диссоциации молекул под влиянием межмолекулярных сил взаимодействия. Кроме того, опытами было доказано, что коэффициенты а и б, входящие в уравнение Ван-дер-Ваальса, описываются достаточно сложными зависимостями от температуры и давления.
Русские ученые М. П. Вукалович и И. И. Новиков в 1939 г. предложили новое универсальное уравнение состояния реального газа, учитывающее явление силовой ассоциации молекул, которое имеет вид
где аиЬ — постоянные уравнения Ван-дер-Ваальса; С,т — постоянные, определяемые на основе опытов.
Видео:Уравнение состояния идеального газаСкачать

Уравнения состояния реальных газов
Вопрос №1
Идеальный газ. Законы идеальных газов
Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы межмолекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.
Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.
Закон Авогадро
Согласно этому закону, все газы при одинаковых температурах и одинаковом давлении содержат в одном и том же объеме одинаковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных газов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м 3 /кмоль.Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.
Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е. при
рV= const и рv = const.
Закон Гей-Люссака
Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если
Р = const, то и v/ Т = const.
Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.
Уравнение состояния идеального газа
Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид
Для одного киломоля вещества уравнение состояния (получено Д.И. Менделеевым) имеет вид рVµ =µRT, где µR— универсальная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.
Во всех этих уравнениях давление подставляется в Па, температура — в К, объем — в м 3 и удельный объем — в м 3 /кг.
В резервуаре объемом 10 м 3 находится азот при избыточном давлении 100 кПа и при температуре 27 °С. Атмосферное давление равно 750 мм рт. ст. Требуется найти массу и плотность азота.
Выразим атмосферное давление в паскалях: рб = 10 5 Па.
Абсолютное давление газа равно:p =ри +рб = 100 • 10 3 + 10 5 = = 2 • 10 5 Па.
Газовая постоянная азота равна (µ = 28 кг/кмоль)
R = 8314/28 = 297 Дж/кгЧК. Масса газа равна
М =рV/RT= 2*10 5* 10/297 • (273,15 + 27) = 22,43 кг.
р = M/V= 22,43/10 = 2,243 кг/м 3 .
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
РЕАЛЬНЫЕ ГАЗЫ
Свойства реальных газов
Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше давление и ниже температура газа. Это объясняется тем, что молекулы реальных газов имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид
где z= φ(р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.
При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энтальпии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависимости от температуры может находиться в разных состояниях.
Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния будем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.
При определенных условиях могут существовать одновременно две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.
У всех веществ фазовые переходы происходят при определенных физических параметрах, поэтому рассмотрение свойств реальных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.
Рассмотрим диаграмму «v—p» воды и водяного пара, на которой изобразим границы между фазами (рис. 1.1). В области а находится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый водяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.
Показанные на рис. 1.1 кривые называются пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насыщенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухого насыщенного пара и кипящей воды называют влажным насыщенным паром. Масса влажного насыщенного пара равна
где М’ — масса кипящей воды и М» — масса сухого насыщенного пара.
В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р’, h’и т.д.), а все параметры, относящиеся к сухому насыщенному пару,— индекс «два штриха» (р’, h» и т.д.).
Температуру и давление насыщенного пара принято обозначать Тн и рн. В то же время в ряде литературных источников их обозначают Тs и рs (буква s является первой буквой английского слова sаturation — насыщение). Отношение массы сухого насыщенного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой пограничной кривой х = 0, а на правой — х = 1. Разность <1-х) называется степенью влажности.
Чем выше давление пара, тем меньше расстояние по горизонтали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насыщенного пара, называется критической (точка к на рис. 1.1).
Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведены в табл. 1
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1 Критические параметры веществ
| Вещество | Tкр, К | pкр,МПа | ρкр, кг/м 3 |
| Азот N2 | 3,40 | ||
| Водород Н2 | 33,2 | 1,29 | |
| Водяной пар H2O | 647,12 | 22,115 | |
| Кислород О2 | 5,05 | ||
| Ртуть Нg | — | ||
| Диоксид углерода СО2 | 7,38 |
При сверхкритическом давлении не может быть влажного насыщенного пара. Если давление пара больше критического и постоянно по величине (р > ркр), то при подводе (или отводе) теплоты физические параметры (удельный объем, энтальпия и др.) меняются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода переходит в сверхперегретый водяной пар.
Уравнения состояния реальных газов
Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде
Слагаемое a/v 2 учитывает внутреннее давление, обусловленное силами взаимодействия молекул газа, а величина b— уменьшение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объемов реальных газов, то уравнение (1) имеет три действительных корня при Т Ткр . Точность вычислений по этому уравнению невелика.
В самой общей форме уравнение состояния реальных газов имеет вид
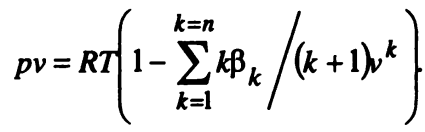
где 𝛽k — вириальные коэффициенты, зависящие от температуры газа.
Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значительные трудности.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
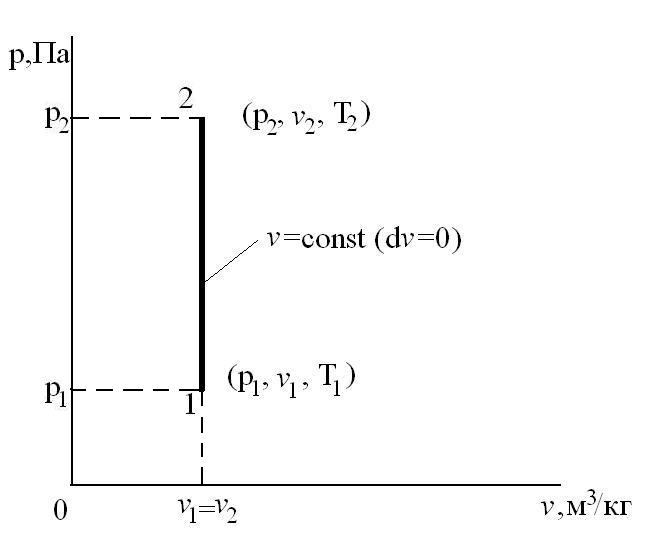
Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 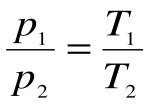
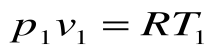
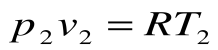
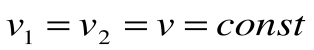
Поскольку работа расширения в этом процессе равна нулю: 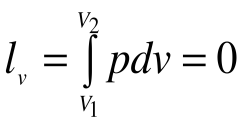
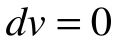
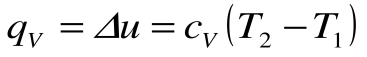
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 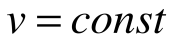
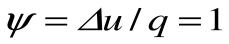


| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
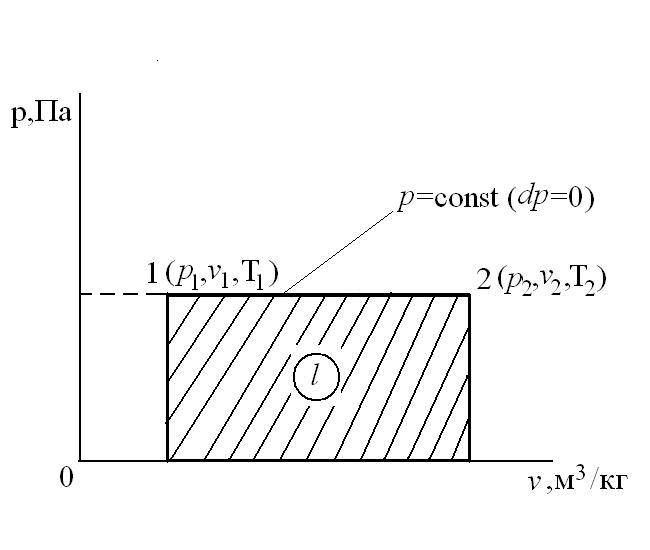
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.
Соотношение между параметрами в процессе р=const: 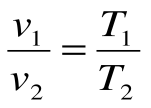


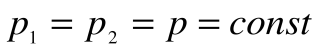
Работа расширения 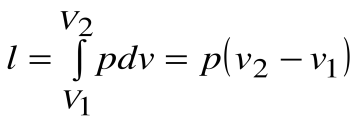
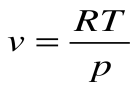
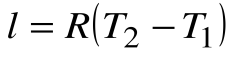
Следовательно, удельная газовая постоянная R— это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
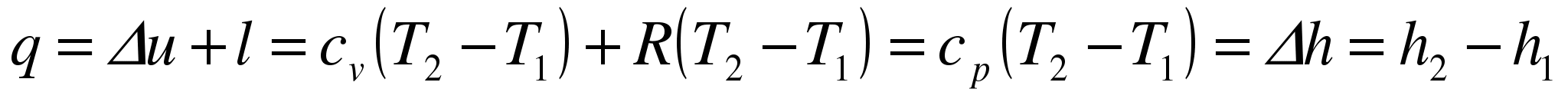
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
Коэффициент распределения теплоты в процессе р=const равен:
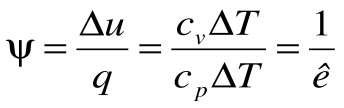
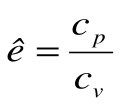
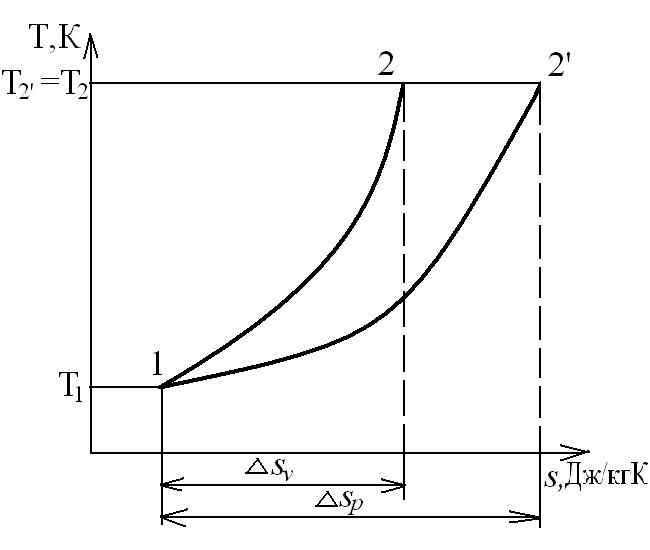
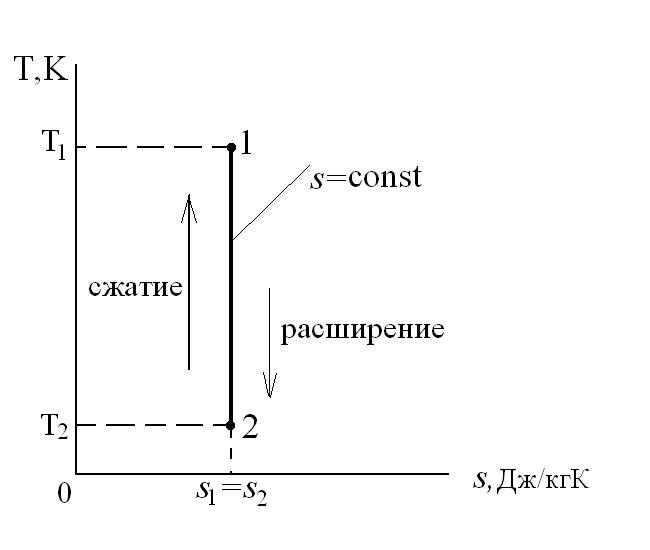
В T-s координатах взаимное положение изобары и изохоры имеет вид:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
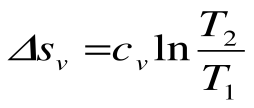
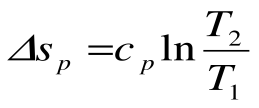
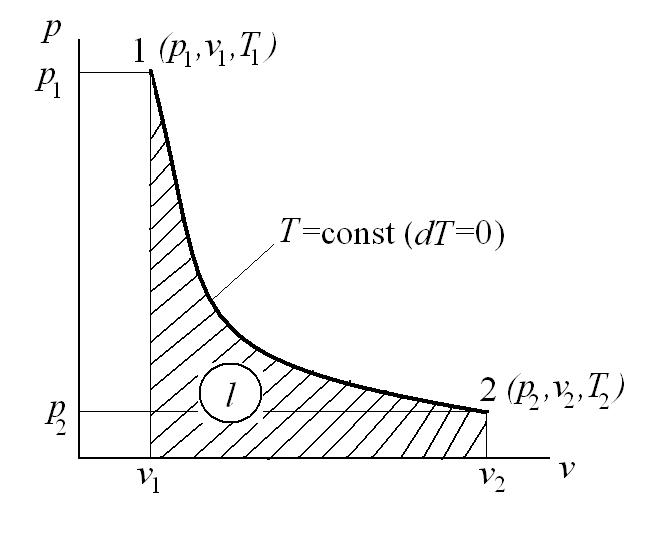
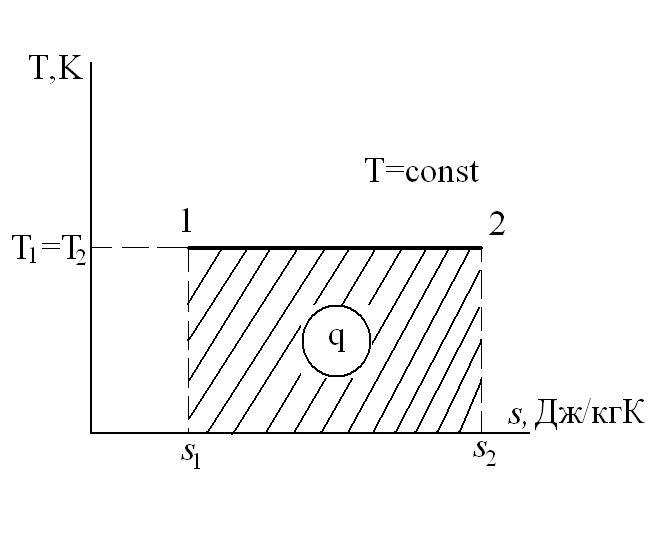
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
При Т=const из уравнения состояния 
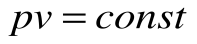
Тогда 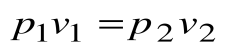
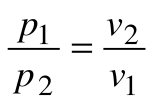
Из уравнения 1-го закона термодинамики 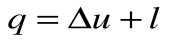
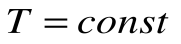
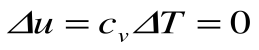
Изменение энтальпии в процессе T=const равно:
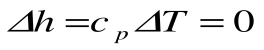
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Работа расширения 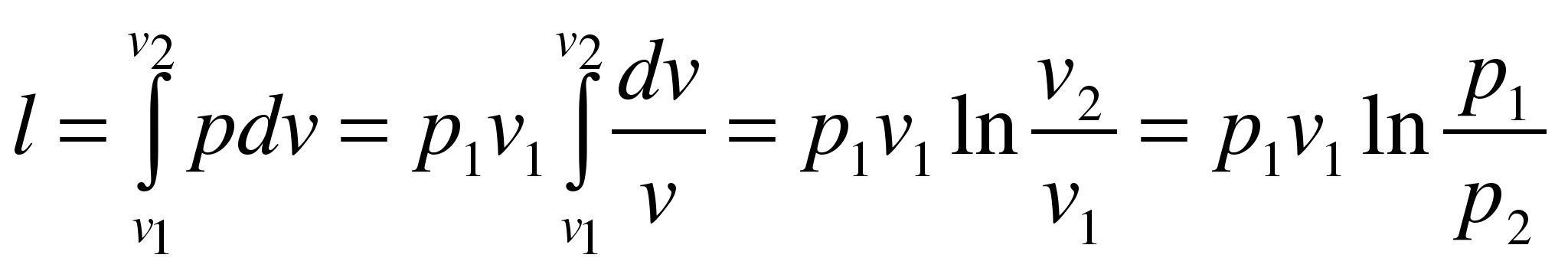
Коэффициент распределения теплоты
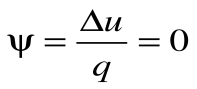
Тогда теплоемкость 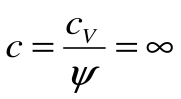
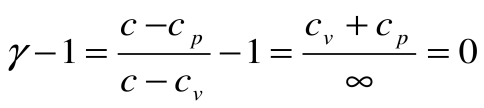
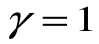
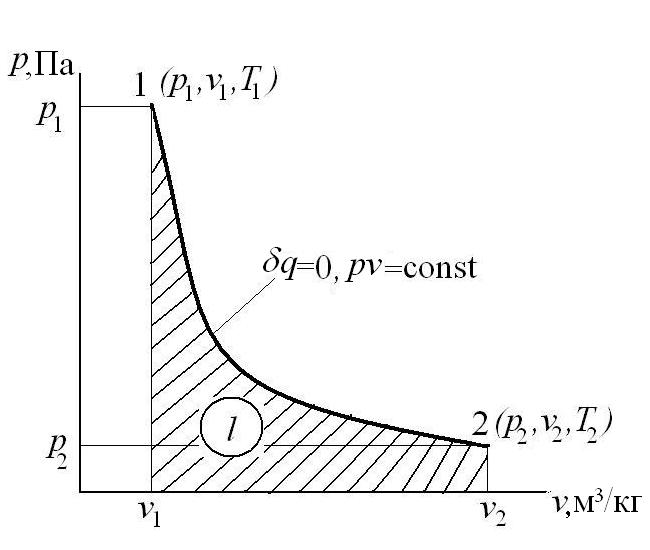
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и 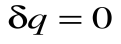
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 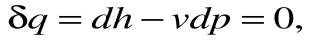
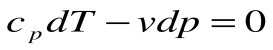
2. 
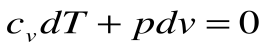

Тогда после интегрирования выражения 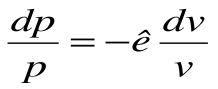

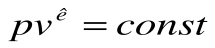
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
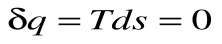
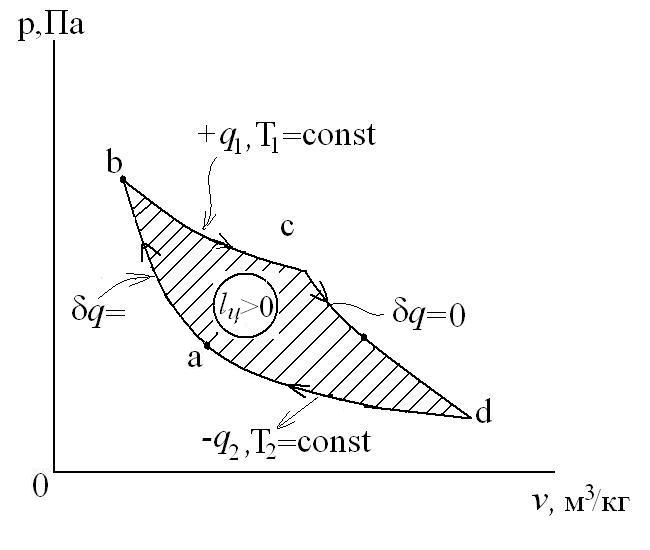
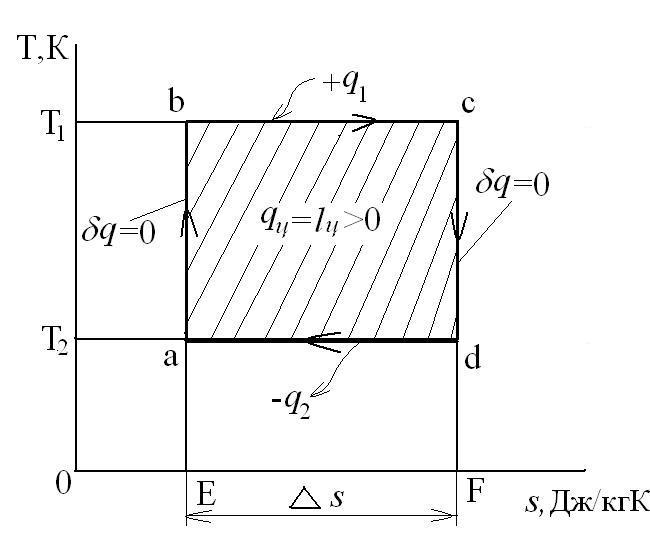
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т1 и Т2.
Рассмотрим прямой цикл Карно.
Графически в p-v и T-s координатах этот цикл можно представить в виде:
где ab – адиабатное сжатие ТРТ;
bc – подвод теплоты q1 в изотермическом процессе при Т1=const;
cd – адиабатное расширение ТРТ;
da – отвод теплоты 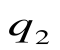
q1 = площадь bсFEb – теплота, затраченная на совершение цикла 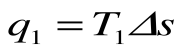
q2 = площадь adFЕa – теплота, отведенная в холодильник 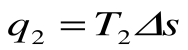
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Тогда термический кпд прямого цикла Карно будет равен:
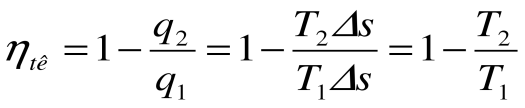
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т1 и Т2 являются основными параметрами цикла Карно, которые полностью определяют этот цикл.
При Т1=Т2 термический кпд цикла Карно 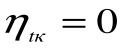
При Т2=0 или Т1= 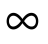
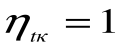
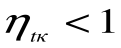
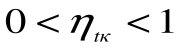
Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.
В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В– водород, объем сосуда А– 150 л, сосуда В – 250 л. Давление и температура аргона – р1, t1, водорода – р2, t2. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнения состояния реальных газов
Все реальные газы являются парами тех или иных жидкостей, причем, чем ближе газ к переходу в жидкое состояние, тем больше его отклонение от свойств идеального газа, состояние которого описывается уравнением Клапейрона. Для качественной оценки особенностей реальных газов рассмотрим область, где будут значительные отступления от уравнения, описывающего поведение идеальных газов.
Если сжимать газ при постоянной температуре, то можно достигнуть состояния насыщения (сжижения газа), соответствующего этой температуре и некоторому определенному давлению. При дальнейшем сжатии пар будет конденсироваться и в определенный момент полностью превратится в жидкость.
Процесс перехода пара в жидкость проходит при постоянных температуре и давлении, так как давление насыщенного пара однозначно определяется температурой. На р – u -диаграмме (рисунок 10.1) область двухфазных состояний (пар и жидкость) лежит между кривыми кипящей жидкости и сухого насыщенного пара. При увеличении давления эти кривые сближаются. Сближение происходит потому, что объем пара, уменьшается, а объем жидкости увеличивается.
При некотором определенном для данной жидкости (пара) давлении кривые кипящей жидкости и пара встречаются в так называемой критической точке, которой соответствуют критические параметры: давление ркр, температура Ткр, удельный объем uкр, характеризующие критическое состояние вещества.
При критическом состоянии исчезают различия между жидкостью и паром. Оно является предельным физическим состоянием, как для однородного, так и для распавшегося на две фазы вещества.
При температуре более высокой, чем критическая, газ ни при каком давлении не может сконденсироваться, т. е. превратиться в жидкость.
В общем случае все газы в области, близкой к состоянию сжижения, приближенно воспроизводят связь между параметрами состояния по уравнению Клапейрона. Во всех газах с более или менее значительной плотностью нельзя пренебрегать силами сцепления между молекулами, объемом, занимаемым ими, а также ассоциацией молекул в группы.
|
|
Уравнение состояния реальных газов выводится или чисто теоретически на основе гипотетических представлений о структуре газа, или на основании обработки экспериментальных зависимостей между р, u, Т.
Широкое распространение в научных исследованиях получило уравнение Ван-дер-Ваальса, выведенное путем пересмотра некоторых допущений, лежащих в основе уравнения состояния идеального газа. Уравнение состояния реального газа с учетом сил, действующих между молекулами, и их объема для 1 кг газа имеет вид
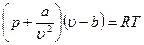
Это уравнение отличается от уравнения Клапейрона двумя поправками: поправкой на объем самих молекул b и поправкой на так называемое внутреннее давление — 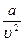
Рассмотрим изменения на изотермах, обусловленных поправками а и b. При температуре выше критической изотермы, построенные по уравнению Ван-дер-Ваальса, представляют собой плавные кривые, отличные от равнобоких гипербол, которые бы дало уравнение состояния идеального газа. Последние в верхней части на рисунка 9.2 показаны пунктиром.
При температуре ниже критической имеется область объемов, где поправка 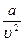
При критической температуре, максимум и минимум на изотермах сливаются в точке перегиба К, а так как касательная к изотерме в критической точке идет горизонтально, то для критической точки должны выполняться условия
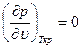
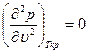
Отсюда получаем уравнения
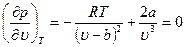
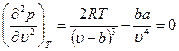
Температуру Ткр и объем uкр можно определить из уравнений (10.3) и (10.4), а давление ркр находится затем из уравнения (10.1). В результате получаем
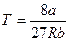
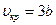

Из последних соотношений можно определить индивидуальные константы а и b, зависящие от физических свойств данного газа
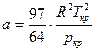
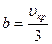
Так как процесс перехода от жидкого состояния к газообразному идет при постоянных Т и р, то на рисунке 10.2 этому процессу соответствует линия АD.
Однако участки АВ и СD на изотермах можно воспроизвести экспериментально только при использовании очень чистых жидкостей и газов. Вещество на этих участках находится в виде перегретой жидкости и перенасыщенного (переохлажденного) пара. Такие состояния, когда вещество остается в однофазном состоянии и не распадается на фазы, называются метастабильными.
Главная ценность уравнения Ван-дер-Ваальса состоит в том, что оно качественно правильно описывает непрерывность перехода из жидкого состояния в газообразное и дальнейшее развитие уравнения состояния пошло по пути уточнения расчетов и усовершенствования его теории.
Предпринимались попытки усовершенствования его за счет того, что коэффициенты а и b принимались не постоянными, а зависящими от температуры и объема. Но эти попытки не привели к созданию уравнения состояния, описывающего свойства газа в широком диапазоне изменения параметров.
Неудачи создания общего уравнения состояния привели к появлению целого ряда эмпирических уравнений, которые могли бы с достаточной точностью предсказывать поведение реальных газов в широком диапазоне условий. Наиболее известны из них: уравнение Битти – Бриджмена с пятью эмпирически определяемыми постоянными и уравнение Бенедикта-Вебб-Рубина, содержащее восемь эмпирических постоянных – (а, b, с, d, А0, В0, С0 и т.д.)
Уравнение Битти – Бриджмена, применяемое до давлений порядка 250 бар и плотностей газа, не превышающих 0,5 плотности в критической точке, имеет вид
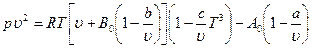
а уравнение состояния Бенедикта – Вебб – Рубина имеет вид
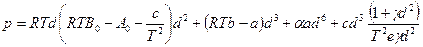
Эти уравнения могут предсказать р, u, Т – свойства газа с ошибкой в пределах нескольких десятых процента и, несмотря на их сложность, развитие вычислительной техники стимулирует использование таких уравнений состояния в обычных технических расчетах.
Хорошо согласуется с опытными данными одно из современных уравнений состояния газа — уравнение Вукаловича — Новикова, учитывающее ассоциацию молекул. При учете столкновений двойных молекул это уравнение имеет вид

где 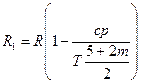
с и m — опытные константы.
В настоящее время теоретически обосновано уравнение состояния, представляющее собой разложение коэффициента сжимаемости z в бесконечный ряд по степеням 1/u
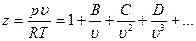
где В, С и D — второй, третий и четвертый вириальные коэффициенты, учитывающие взаимодействие соответственно двух трех, четырех и т. д. молекул. Вириальные коэффициенты зависят лишь от температуры и определяются, если известна зависимость потенциальной энергии взаимодействия молекул U от расстояния между ними (рисунок 10.3).
Вместо точных аналитических зависимостей Uпот= f(r) практически применяют приближенные выражения, которые называются потенциалами. Широко используется потенциал Леннарда — Джонса, по которому энергия отталкивания пропорциональна двенадцатой степени расстояния между молекулами, а энергия притяжения – шестой
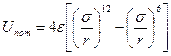
где r — расстояние между молекулами; s— значение r, при котором Uпот = 0; e – максимальная величина энергии притяжения (глубина потенциальной ямы).

|
При решении целого ряда технических задач рабочими телами могут быть не широко используемые в технике вещества (водяной пар, углекислый газ, азот и некоторые другие), а вещества, термические свойства которых неизвестны.
В этом случае можно воспользоваться для предсказания свойств малоизученных веществ положением о термодинамическом подобии веществ.
Если значения индивидуальных констант а и b подставить в уравнение (10.1), то получим уравнение Ван-дер-Ваальса в функции приведенных параметров

где 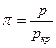

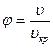
Эти отношения называются приведенными давлением, температурой и объемом. Уравнение (10.12) можно записать в форме

В этой форме приведенное уравнение состояния будет одинаково для всех веществ. Состояния двух или нескольких веществ, в которых они имеют одинаковые приведенные параметры 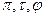
Если вещества подчиняются одному и тому же приведенному уравнению состояния и имеют два одинаковых приведенных параметра, то у них одинаков и третий приведенный параметр, т. е. вещества, будут находиться в соответственных состояниях. Это положение носит название закона соответственных состояний.
Вещества, подчиняющиеся закону соответственных состояний, называют термодинамически подобными.
Практически закон соответственных состояний наиболее удобно применять в виде зависимости 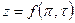
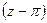
Для этого, зная критические параметры вещества, находят 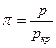

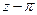
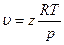
Точность расчета по этому методу не превышает 15%, так как закон соответственных состояний выполняется лишь приближенно. Так, при одинаковых я и т коэффициенты сжимаемости должны быть равны, причем должны быть равны и коэффициенты сжимаемости в критической точке 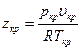
Парообразование при постоянном давлении
Рассмотрим изменение состояния водяного пара (реального газа), имеющего сравнительно высокую критическую температуру. Изменение параметров состояния водяного пара удобно проследить на р-u -диаграмме (рис. 9.5).
Положим, что 1 кг воды при 0° С заключен в цилиндре, закрытом свободно движущимся невесомым поршнем, на который действует постоянное внешнее давление. Объем воды при указанных условиях обозначим 
Если (при постоянном давлении) подводить к жидкости теплоту, то при достижении температуры кипения tВ начнется превращение воды в пар — точка т. Удельный объем жидкости вследствие нагрева увеличивается от 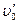
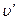
На р-u -диаграмме геометрическое место точек, определяющих состояние воды, нагретой до температуры кипения, изображается кривой т¢, т, т². Эту кривую называют нижней (левой) пограничной кривой. При дальнейшем подведении теплоты начинается процесс парообразования. При условии постоянства давления, как показывает опыт, для всех жидкостей имеет место характерное явление: температура смеси жидкости и пара остается неизменной и равной температуре кипения tH.

Влажный насыщенный пар представляет собой смесь пара с жидкостью, причем жидкость может быть сосредоточена в нижней части цилиндра или равномерно распределена в виде мельчайших капель по всему объему.
Пар, полученный при испарении всей жидкости (точка п), — сухой насыщенный. Удельный объем, пара в этой точке обозначим через u». При проведении процесса парообразования при другом давлении соответственно получим точки n¢, п». Кривая п’ п п» представляет собой верхнюю (правую) пограничную кривую. Пересечение верхней и нижней пограничных кривых определяет положение критической точки К. Для воды критической точке соответствует ркр = 221,048 бар, Ткр = 647,15° К; uкр = 0,0031 м 3 /кг. На рис. 9.5 в области влажного насыщенного пара пунктирными линиями показаны линии постоянной сухости. Степень сухости пара х представляет собой массовую долю сухого насыщенного пара во влажном
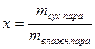
Для точек, лежащих на нижней пограничной кривой, х = 0, для точек, лежащих на верхней пограничной кривой, х = 1. Если к сухому насыщенному пару продолжать подводить теплоту, то удельный объем и температура увеличиваются (un > u», t > tн). Пар в этом состоянии называют перегретым. Начиная с точки п вправо система однофазная.
Изменение агрегатного состояния

Состояния вещества при этих превращениях считают устойчивыми, стабильными. При этом всякие изменения состояния считаются квазистатическими, как это обычно принято в термодинамике.
Переход из одного агрегатного состояния в другое удобно рассматривать на р – t — диаграмме (рис. 9.6). На диаграмме кривая АК представляет собой зависимость между давлением насыщенного пара и температурой кипения, т. е. р = f (tн) (кривая упругости пара).
Кривая равновесия жидкой и газообразной фазы заканчивается в критической точке К.
Если от жидкости отбирать теплоту при постоянном давлении, то при определенной температуре жидкость переходит в твердое состояние. Температура, при которой осуществляется этот переход, называется температурой затвердевания, или плавления tпл, а количество теплоты, отбираемое в этом процессе, называется скрытой теплотой плавления. При плавлении так же, как и при парообразовании, вещество находится в двух фазах. Аналогично кривой АК можно построить кривую AD, которая однозначно определяется зависимостью р = f(tпл).
Кривая сублимации АВ представляет собой зависимость р = f(tc) для перехода твердого тела в газообразное. Этот переход при температуре сублимации tc происходит вследствие подведения некоторого количества теплоты, носящего название скрытой теплоты сублимации. Точки этой кривой соответствуют двухфазной системе твердое тело — газ (например, водяной пар над поверхностью льда).
Все три кривых равновесия (парообразования, плавления и сублимации) пересекаются в некоторой характерной для каждого вещества точке. Эта точка А называется тройной точкой, а изображаемое ею состояние — фундаментальным. В этой точке находятся в термодинамическом равновесии три различные фазы вещества: твердая, жидкая и газообразная.
Тройной точке воды соответствуют следующие параметры: давление р = 0,00610 бар, Т =273,16°К.
Рассмотрение описанных процессов показывает, что в состояниях, находящихся между кривыми АВ, АЕ и AD, тело будет находиться целиком в одной фазе: правее АВ и АК — область газообразного состояния; левее линий AD и АВ располагается область вещества в твердом состоянии; между линиями AD и АК находится область жидкости.
В состояниях на линии АК, AD и АВ вещество может существовать в двух фазах, причем на линии АК в жидкой и газообразной, на AD —твердой и жидкой; а на линии АВ вещество может быть в твердом и газообразном состояниях. Расположение и вид этих трех кривых
зависят от природы вещества и устанавливаются опытным путем.
Параметры состояния воды и водяного пара
Вследствие незначительной сжимаемости воды можно принять, что плотность воды при 0° С и любых давлениях есть величина постоянная, a u’0 = 0,001 м 3 /кг. Начало отсчета внутренней энергии энтальпии и энтропии берется от 0° С и соответствующего давления насыщения р = 0,00610 бар. При этих параметрах энтальпия, энтропия, а также внутренняя энергия воды берутся условно равными нулю: s’0 = 0, i’0 = 0, и’0 = 0.
В процессе подогрева воды происходит нагревание ее до температуры кипения tн. Удельный объем воды при температуре кипения u’ будет больше объема u’0. Соответствующие значения u’ для воды в функции температуры и давления для состояний, лежащих или на нижней пограничной кривой, или левее ее, даются в справочной литературе.
Количество теплоты, которое нужно сообщать воде, чтобы нагреть ее от 0° С до температуры кипения в процессе р = const, называется теплотой жидкости. Это количество теплоты определяется по формуле
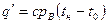
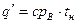
где 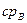
При низких по сравнению с Ткр температурах можно считать 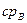
Воспользуемся в изобарном процессе подогрева воды первым за’ коном термодинамики, по которому
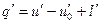
где и’ — внутренняя энергия воды при температуре кипения.
Так как при 0° С и¢0 = 0, а работа расширения жидкости
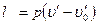
практически заметна только при больших значениях давления, то
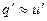
Энтальпия воды при температуре кипения определяется по общей формуле
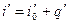
Полагая, что 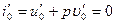
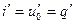
В процессе нагревания жидкости от 0° С до температуры кипения происходит увеличение ее энтропии, которое может быть найдено по формуле
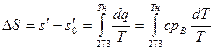
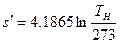
Как уже было сказано, опытами установлено, что в процессе парообразования жидкость, нагретая до температуры кипения при . этой температуре и определенном постоянном давлении, обращается в пар. Количество теплоты, затрачиваемое в процессе при р = const на превращение 1 кг воды при температуре кипения в сухой насыщенный пар той же температуры, обозначим через г.
Теплота г называется скрытой теплотой парообразования. По первому закону термодинамики
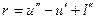
где и²— внутренняя энергия сухого насыщенного пара;
l» — работа расширения в процессе парообразования.
Разность внутренних энергий и» — и¢ затрачиваемая на работу против внутренних сил, называется внутренней теплотой парообразования и обозначается буквой r. Теплота, затрачиваемая на работу против внешних сил, равна
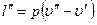
и называется внешней теплотой парообразования. Обозначим ее буквой y.
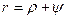
Вследствие того, что процесс парообразования идет при постоянном давлении,
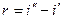
Величины r и i» даются в таблицах насыщенного пара, а 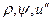
С возрастанием давления, как видно из рис. 9.7, увеличивается энтальпия жидкости и достигает максимального значения при критическом давлении. Скрытая теплота парообразования уменьшается с ростом давления и равна нулю при критическом давлении (и температуре), потому что в этих условиях различия между жидкостью и ее паром исчезают и процесс парообразования как таковой отсутствует.
Изменение энтропии в процессе парообразования при подведении к кипящей воде r кдж/кг теплоты равно
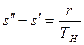
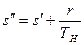
или, используя значение s¢ из выражения (9.23),
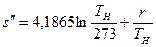

Связь между удельными объемами жидкости и пара на линии насыщения u¢ и u² давлением насыщенного пара рН температурой ТН и скрытой теплотой парообразования может быть получена следующим образом. При превращении жидкости в пар давление насыщенного пара от объема системы не зависит, следовательно, в выражении (8.8) 
где dV представляет изменение объема системы при переходе жидкости в пар. Таким образом,
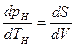
Изменение объема системы, если испарилась жидкость массой dm, равно
а приращение энтропии в квазистатическом процессе испарения жидкости массой dm по (9.28)
Подставив эти значения в уравнение (9.31), получим
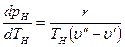
где 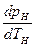
Уравнение (9.32) называют уравнением Клапейрона—Клаузиуса и применяют при исследованиях изменений агрегатного состояния вещества из жидкого состояния в парообразное. Аналогичные уравнения можно применять и к процессам перехода вещества из твердого состояния в жидкое или газообразное.
Параметры влажного насыщенного пара при заданной величине сухости могут быть определены из следующих соотношений.
Удельный объем влажного насыщенного пара
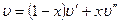
Так как объем воды (1 — х) 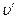
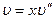
Энтальпия влажного насыщенного пара с учетом того, что на превращение в пар х кг жидкости необходимо затратить хr кдж/кг теплоты, равна
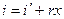
Энтропия влажного насыщенного пара
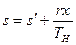
Свойства перегретого пара резко отличаются от свойств насыщенного пара и приближаются к свойствам газов.
Перегретый пар характеризуется тем, что его температура выше температуры парообразования ТH при том же давлении и удельный объем его больше, чем объем сухого насыщенного пара при том же давлении.
Количество теплоты, необходимое для перевода 1 кг сухого насыщенного пара при р = const в перегретый с температурой t, называют теплотой перегрева qпи определяют по формуле
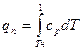
Если срm — средняя массовая теплоемкость перегретого пара при постоянном давлении, то
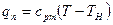
Значение срm берется для перегретого пара по формуле
Энтальпия перегретого пара
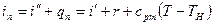
называется полной теплотой перегретого пара. По первому закону термодинамики
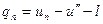
где 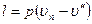
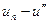
Изменение энтропии в равновесном изобарном процессе перегрева равно

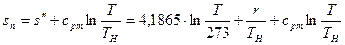
Свойства перегретых паров будут тем ближе к свойствам идеального газа, чем больше температура перегрева.
Т—s-диаграмма водяного пара
Для графического изображения процессов, происходящих в паре, удобно пользоваться Т — s-диаграммой, ибо в ней площадь под кривой обратимого процесса дает количество теплоты, сообщаемое телу или отнимаемое от него. Так как в системах координат р — v и Т—s любая точка изображает определенное состояние тела, то точкам р- 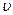
Если было принято условно, что энтропия начального состояния воды so = 0, то эта точка лежит на оси ординат на 273° выше абсолютного нуля.
Перенося по точкам нижнюю пограничную кривую (х = 0) из системы р — v в Т — s-диаграмму, получим соответствующую ей кривую, абсциссами которой являются значения s’. Аналогично наносится верхняя пограничная кривая (х = 1), абсциссами которой будут значения энтропии сухого насыщенного пара s».
В точке b диаграммы начинается кипение при ТH = const, и энтропии в процессе парообразования повышается
Процесс парообразования заканчивается в точке с, где
Так как процесс парообразования идет при Тн = const и р — =const, изотерма b-с является одновременно и изобарой. Дальнейший подвод теплоты снова сопровождается увеличением температуры и энтропии. В процессе перегрева пара (кривая с-е)

Учитывая, что количество теплоты в процессе р = const равно разности энтальпий 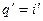
Область, лежащая между кривыми аК и сK, — это область влажного насыщенного пара. Область, лежащая правее верхней пограничной кривой, — область перегретого пара.
Исследования паровых процессов и расчеты существенно облегчаются при наличии подробной Т — s-диаграммы, в которой нанесены обе пограничные кривые, сетка изобар и изохор, а также кривые постоянной сухости х = const, которые на рис. 9.8 показаны пунктирными линиями.
§ 6. i—s-диаграмма водяного пара

В системе координат i — s наносятся пограничные кривые, изобары и изотермы. Нижняя пограничная кривая и верхняя пограничная кривая строятся по известным значениям 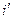
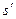
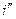
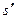
равна разности ординат точек пересечения изобары с правой и левой пограничными кривыми.
Для процесса парообразования, происходящего при р = const,
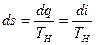
Следовательно, в области влажного насыщенного пара изобары, являясь одновременно и изотермами, представляют собой прямые линии с угловым коэффициентом, равным Tн; из диаграммы видно, что изобары пересекают пограничные кривые без излома. Изохоры, изобары и изотермы в области перегретого пара строятся по точкам. Изобары и изохоры в области перегрева — слабо вогнутые логарифмические кривые; изотермы в области перегретого пара — выпуклые кривые, поднимающиеся слева вверх направо. Вид изотерм определяется температурой, которой они соответствуют. Чем больше температура, тем выше располагается изотерма. Чем дальше от пограничной кривой (х = 1) проходит изотерма, тем больше она приближается к горизонтали i = const, так как в области идеального газа энтальпия однозначно определяется температурой. На рис. 9.9 точки A, В, С изображают соответственно состояния влажного, сухого и перегретого пара. Причем точка А лежит на пересечении изобары (изотермы) и линии постоянной сухости, точка В лежит на пересечении изобары и верхней пограничной кривой, точка С находится на пересечении изобары и изотермы. По положению точки, соответствующей некоторому состоянию пара, можно определить на i — s-диаграмме числовые значения всех параметров в этой точке.
Большинство газов, применяемых в технике, содержит пары тех или иных жидкостей. Наиболее распространенными являются смесь воздуха или какого-либо другого газа с водяным паром, смесь воздуха с парами бензина, керосина и т. п.
Характер изменения параметров парогазовой смеси имеет важное значение в расчетах процесса сушки, кондиционирования воздуха, сверхзвуковых аэродинамических труб, обледенения самолетов, процесса испарения топлива в двигателях и форсировании их впрыском жидкостей и т.д.
Смесь, состоящая из сухого газа и перегретого пара, называется ненасыщенным влажным газом, а смесь из сухого газа и насыщенного пара — насыщенным влажным газом.
При охлаждении влажного газа до определенной температуры (температуры точки росы) пар становится насыщенным, а в дальнейшем может и сконденсироваться.
Состояние парогазовой смеси определяется сравнительно узким диапазоном температуры и давления. Значительное повышение температуры или понижение давления приводит к тому, что влажный газ превращается в простую газовую смесь (гл. 11, § 4).
Полагая, что перегретый пар любой жидкости, входящий в состав влажного газа, приближается по своим свойствам к газам, можно рассматривать влажный газ как газовую смесь.
По закону Дальтона давление смеси идеальных газов р равно сумме парциальных давлений
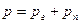
где pv — парциальное давление сухого газа; рп — парциальное давление пара.
Равным образом можно записать
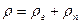
Равенство (9.44) показывает, что плотность влажного газа выше плотности сухого тогда, когда давление влажного газа по уравнению (9.43) выше сухого.
Основными характеристиками влажного состояния газа являются:
относительная влажность j, которая определяет степень насыщения газа паром
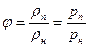
где рп и рн — плотности перегретого и насыщенного пара;
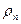
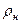
Соотношение (9.45) справедливо только тогда, когда можно считать, что пар жидкости является идеальным газом вплоть до состояния насыщения. При этом
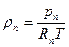
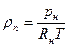
где Rп = Rн — газовая постоянная пара;
абсолютная влажность D, определяющая массу пара, содержащегося в 1 м 3 газа,
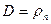
влагосодержание d — это масса пара, содержащегося в 1 кг сухого газа,
или, определяя рп и рг из уравнения состояния, получим
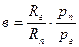
Рассматривая влажный газ как газовую смесь, выведем соотношения, связывающие параметры влажного газа. Пусть состояние, влажного газа определяется его давлением р, температурой t, плотностью r и относительной влажностьюj. По таблицам сухого насыщенного пара определяем для данной температуры значения rн и рн.
Плотность пара в смеси по уравнению (9.45) равна
а плотность сухого газа
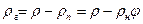
Парциальное давление сухого газа можно определить из уравнения состояния
Парциальное давление пара в смеси
Если заданы для влажного газа р, t, 
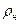
Парциальные давления пара и сухого газа вычислим по формулам

Плотность сухого газа найдем из уравнения состояния
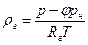
а плотность влажного газа вычислим по формуле (9.44). Влагосодержание на 1 м 3 и на 1 кг сухого газа определяют по формулам:
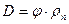
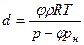
Если газ насыщен паром, то j = 1 и
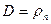
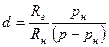
Массовые доли сухого газа и пара во влажном газе соответственно равны:
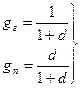
Используя обычное выражение газовой постоянной для смеси газов (гл. 11, § 4), получим
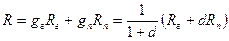
Теплоемкость влажного газа можно определить, зная массовый состав его и теплоемкости сухого газа и пара,
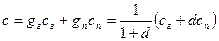
Так же, как и теплоемкость, энтальпия влажного газа равна сумме энтальпий сухого газа и пара. Следовательно,
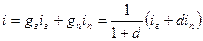
Энтальпия 1 кг сухого газа
Энтальпия водяного пара, который находится в перегретом состоянии, определяется по формуле
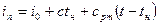
где i0+ctн — энтальпия сухого насыщенного пара в газе (tн— температура кипения при определенном парциальном давлении); срт — средняя теплоемкость перегретого пара.
Для водяного пара iп может быть взята из таблиц водяного пара. Таким образом, энтальпия влажного насыщенного пара равна
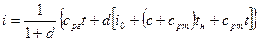
Тепловые процессы парогазовой смеси имеют ряд особенностей, их можно разделить на:
процессы, идущие без фазовых превращений, в этом случае относительная влажность j р2 > р3 и т. д.), изохоры <u1 > u2 > u3 и т. д.), изотермы (t1
Дата добавления: 2015-04-03 ; просмотров: 3376 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔍 Видео
Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Уравнение состояния идеального газаСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

10 класс урок №39 Уравнение состояния идеального газаСкачать

Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Идеальный газ / Perfect gasСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать