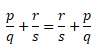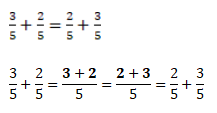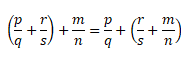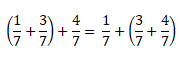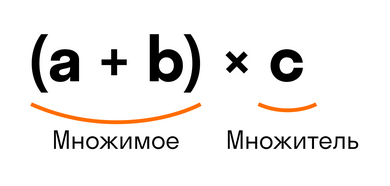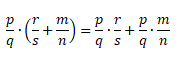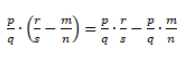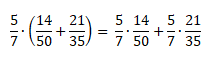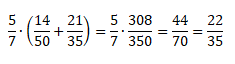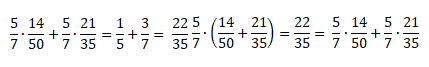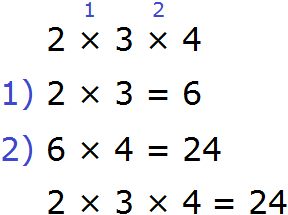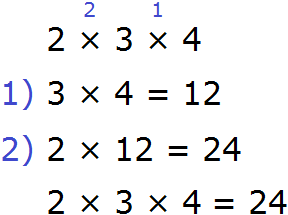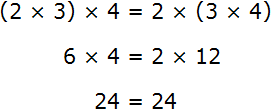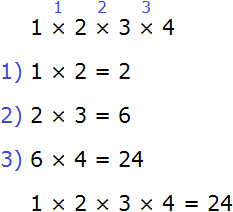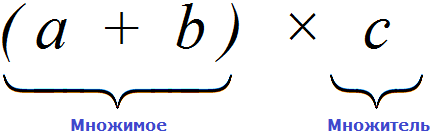Укажите уравнение соответствующее распределительному закону

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Распределительный закон умножения. Объяснение. МАТЕМАТИКА 6 класс. Много примеров.Скачать

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним. Вот так:

Видео:Математика 5 класс (Урок№9 - Распределительный закон.)Скачать

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

1. Результат сложения нескольких слагаемых не зависит от порядка действий.
2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

• 1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

• 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Распределительный закон умножения относительно сложения и вычитания 5 классСкачать

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Видео:Раскрытие скобок. 6 класс.Скачать

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

• 3 * 4 = 12
• 2 * 12 = 24
• 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

• (2 * 3) * 4 = 2 * (3 * 4)
• 6 * 4 = 2 * 12
• 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 * 7 * 8 = 1680

Видео:6 класс, 15 урок, Применение распределительного свойства умноженияСкачать

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

• Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
• Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

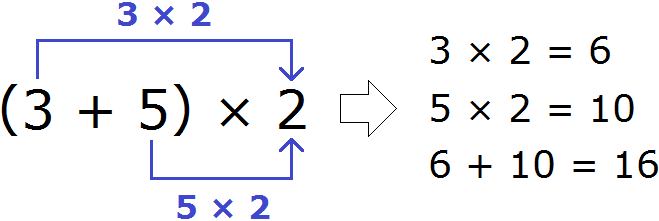
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

• (3 + 5) * 2 = 3 * 2 + 5 * 2
• 3 * 2 = 6
• 5 * 2 = 10
• 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

Пример 1

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

Пример 3

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Видео:Математика 6 класс (Урок№29 - Распределительный закон.)Скачать

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Видео:РАСПРЕДЕЛИТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯСкачать

Законы математики

В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.

У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае — к тому что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.

Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.

В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.

Видео:Распределительный законСкачать

Переместительный закон сложения

Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:

Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс.

Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.

Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:

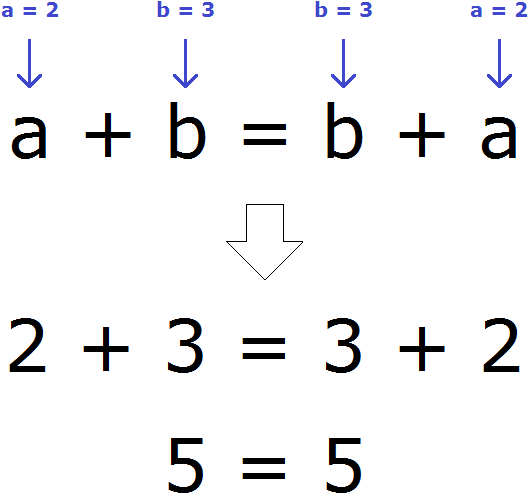
Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:

Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3 . Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а , число 3 место b

Видео:МАТЕМАТИКА 6 класс: Применение распределительного свойства умноженияСкачать

Сочетательный закон сложения

Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.

Рассмотрим сумму из трёх слагаемых:

Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:

2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10

Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2

2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10

Видно, что в обоих случаях получается один и тот же результат.

Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(2 + 3) + 5 = 2 + (3 + 5)

Запишем сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Видео:Сочетательное и распределительное свойство умножения. 5 классСкачать

Переместительный закон умножения

Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.

В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 × 2 = 2 × 5

Запишем переместительный закон умножения с помощью переменных:

Для записи законов в качестве переменных необязательно использовать именно буквы a и b . Можно использовать любые другие буквы, например c и d или x и y . Тот же переместительный закон умножения можно записать следующим образом:

Видео:Математика 5 класс (Урок№64 - Законы умножения. Распределительный закон.)Скачать

Сочетательный закон умножения

Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

Рассмотрим следующее выражение:

Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:

Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2

Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

Запишем сочетательный закон умножения с помощью переменных:

a × b × с = (a × b) × с = a × (b × с)

Пример 2. Найти значение выражения 1 × 2 × 3 × 4

Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:

Видео:Распределительный законСкачать

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

Рассмотрим следующее выражение:

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

(3 + 5) × 2 = 6 + 10 = 16

Теперь запишем распределительный закон умножения с помощью переменных:

(a + b) × c = a × c + b × c

Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.

Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×

Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b) . Тогда получится, что мы умножаем переменную c на сумму (a + b) . Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.

Пример 4. Найти значение выражения 5 × (6 − 2)

Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Пример 5. Найти значение выражения 7 × (3 − 2)

Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

Видео:5 класс Распределительный закон умноженияСкачать

Свойства операций над высказываниями

п.1. Переместительные, сочетательные и распределительные законы алгебры высказываний

При определении конъюнкции и дизъюнкции (см. §31 данного справочника), мы указали, что конъюнкция является логическим умножением, а дизъюнкция – логическим сложением.

Ещё из курса арифметики, нам известно, что операции умножения и сложения для чисел обладают коммутативностью (переместительный закон), ассоциативностью (сочетательный закон) и дистрибутивностью (распределительный закон) (см. §2 справочника для 7 класса). Эти же законы справедливы в алгебре высказываний.

🎦 Видео

Распределительный закон и Вынесение за скобки общего множителя ( Математика - 5 класс )Скачать

Дроби. Умножение. Распределительный закон. 5 классСкачать

Применение распределительного свойства умножения 6 классСкачать

Переместительный и сочетательный законы умножения. Примеры их применения.Скачать

Законы умножения. Распределительный законСкачать

Распределительный закон умножения. 5 класс. Уроки с АркадиемСкачать

Распределительный закон (часть 2)Скачать