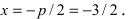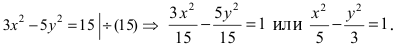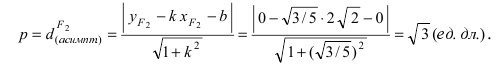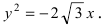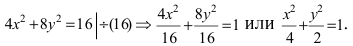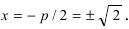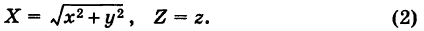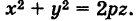Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
- Что такое парабола и как она выглядит
- Каноническое уравнение параболы
- Свойства и график квадратичной функции
- Как определить, куда направлены ветви параболы
- Как найти вершину параболы по формуле
- Смещение параболы
- Как строить параболу по квадратному уравнению
- Директриса, эксцентриситет, фокус параболы
- Заключение
- Парабола — определение и вычисление с примерами решения
- Уравнение параболоида вращения
- Как определить a, b и c по графику параболы
- 1 способ – ищем коэффициенты на графике
- 3 способ – используем преобразование графиков функций
- 📸 Видео
Видео:Как легко составить уравнение параболы из графикаСкачать

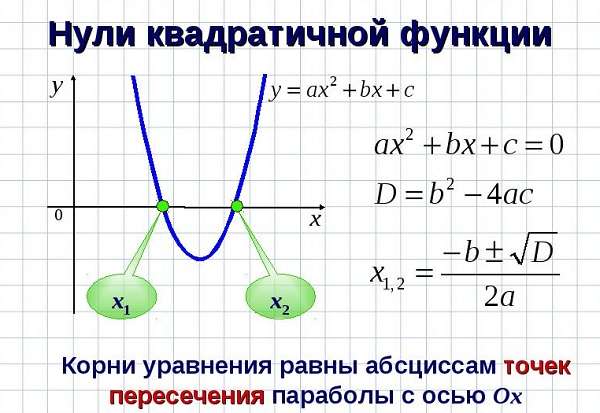
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
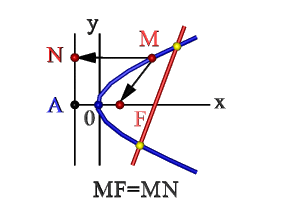
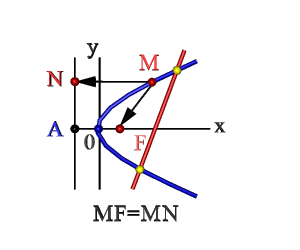
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Видео:Известно, что парабола проходит через точку В(-1; -1/40, и её вершина находится в начале координатСкачать

Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Видео:Как определить уравнение параболы по графику?Скачать

Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Видео:§24 Каноническое уравнение параболыСкачать

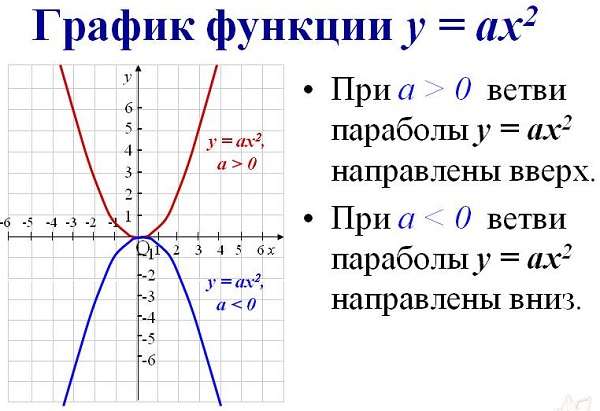
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Видео:Фокус и директриса параболы 1Скачать

Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Видео:213. Фокус и директриса параболы.Скачать

Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Видео:Построение параболыСкачать

Директриса, эксцентриситет, фокус параболы
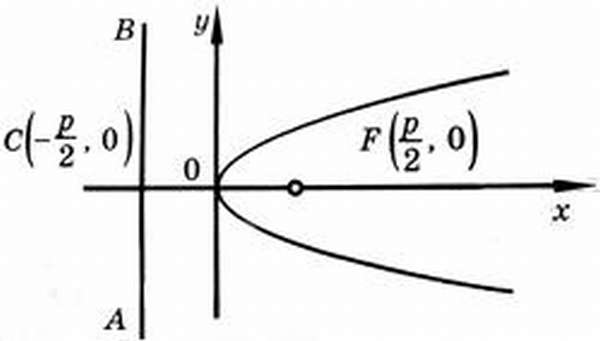
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.
Эксцентриситет (константа) = 1.
Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Парабола — определение и вычисление с примерами решения
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
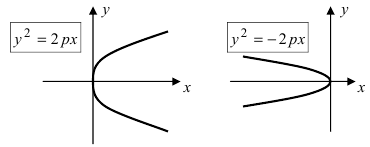
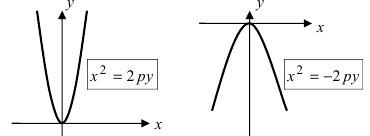
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы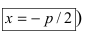
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 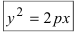
Рис. 35а. Параболы и их уравнения.
Рис. 356. Параболы и их уравнения.
Найдем координаты точек пересечения параболы с координатными осями:
— точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью ординат.
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 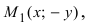
Пример:
Дано уравнение параболы 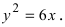
Решение:
Так как из уравнения параболы 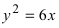
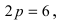
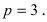
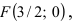
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 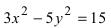
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 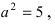
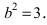
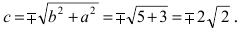
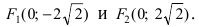
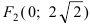
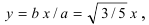
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 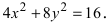
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 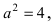
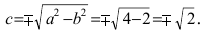
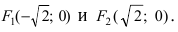
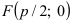
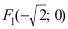
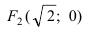

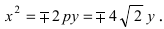
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

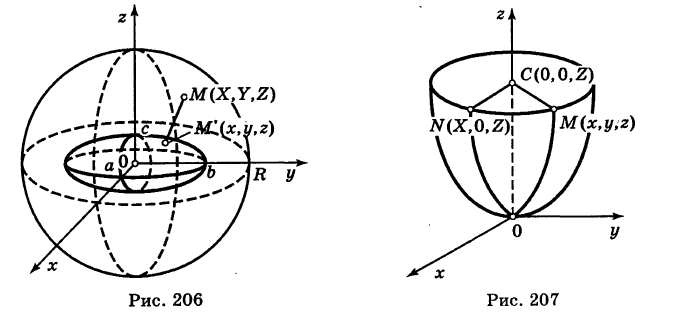
Уравнение параболоида вращения
Пусть вертикальная парабола
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

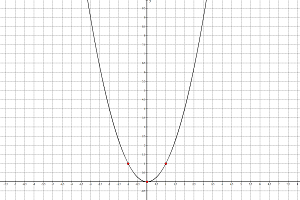
Как определить a, b и c по графику параболы
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
Видео:Парабола. Квадратичная функцияСкачать

3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
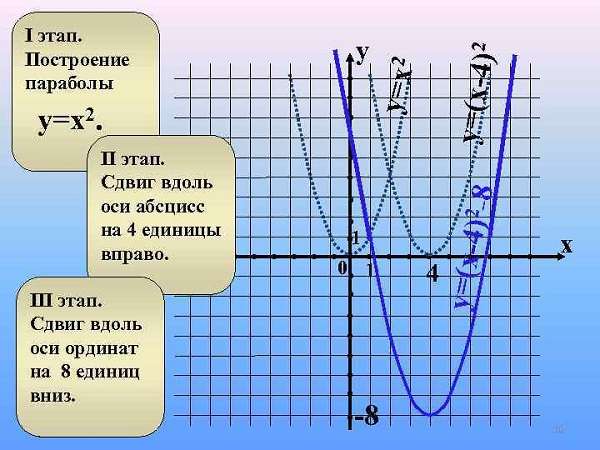
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).
То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
📸 Видео
Как найти вершину параболы?Скачать

Вершина параболы и ось симметрии. ПримерСкачать

Как строить параболу? | TutorOnlineСкачать

Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.Скачать

Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать



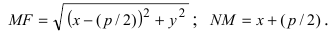
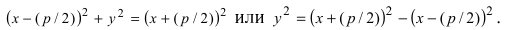
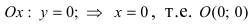 — точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью абсцисс;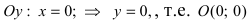 — точка пересечения параболы с осью ординат.
— точка пересечения параболы с осью ординат.