Укажите уравнение окружности центр которой имеет координаты 3 6 а радиус равен 5

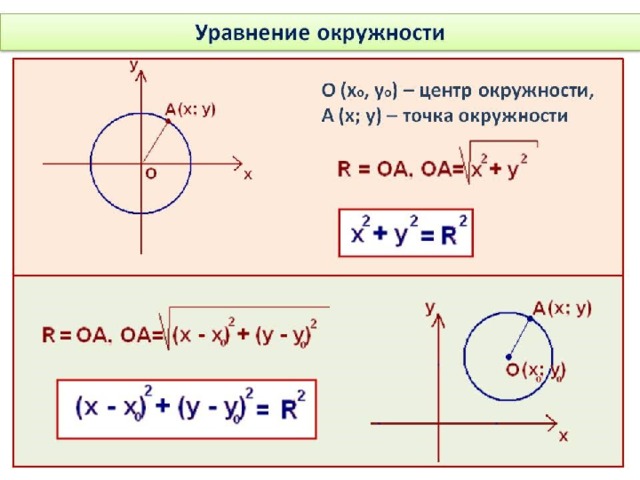
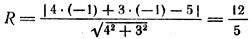Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:Уравнение окружности (1)Скачать

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

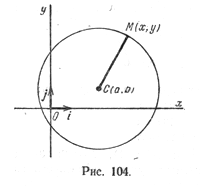
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

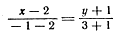
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

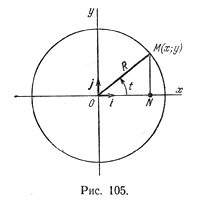
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»

В презентации к уроку геометрии для 9 класса представлены задачи по теме «Уравнение окружности».

Просмотр содержимого документа
«Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»»

Определите по уравнению окружности координаты ее центра и радиус :

А) (Х+2)² + ( У – 5)² = 49

Б) (Х+7)² + ( У + 1)² = 36

Ответ : О (-7; -1); R= 6

В) (Х- 6)² + ( У + 15)² = 81

Ответ : О (6; -15); R= 9

Ответ : О (0; 9); R= V͞2

Составьте уравнение окружности, если известны координаты ее центра М и радиус R :

В) М ( 1; -1) , R = ; = V͞11

Задание № 2 ( проверка)

Составьте уравнение окружности с центром в точке М (1; -4), проходящей через точку А(0; 3).

Составьте уравнение окружности, диаметром которой является отрезок АВ,

если А( -4; 7), В ( 2; 5 )

Составьте уравнение окружности, радиусом которой является отрезок КР,

если К (-2; 3), Р ( 5; — 23)

Составьте уравнение окружности с центром в точке

А(-4; 2), которая касается оси ординат.

Составьте уравнение окружности, проходящей через точку А( 1; -5 ), центр которой принадлежит оси абсцисс, а радиус равен 13.

Докажите, что данное уравнение является уравнением окружности, и укажите координаты центра и радиус этой окружности:

А) Х² + У² + 6х – 14у – 5 = 0;

Найдите координаты центра и радиус окружности ,заданной уравнением

Х² + У² — 18х +2у + 50 = 0. Определите положение точек

А(5; -1), В(2; 4) и С( 13; — 5 ) относительно этой окружности.

📽️ Видео

Найти центр и радиус окружностиСкачать

№965. Напишите уравнения окружностей с центром в начале координат и радиусами r1=3, r2= √2 , r3=5/2.Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

Задачи на уравнение окружности. Уравнение окружности. Урок 2. Геометрия 8 класс.Скачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Уравнение окружностиСкачать

Уравнение окружности | Окружность | Математика 9 класс | Мегашкола | Геометрия 9 класс | Мерзляк 9Скачать

9 класс, 7 урок, Уравнение прямойСкачать

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать