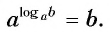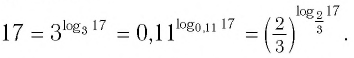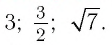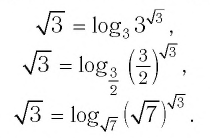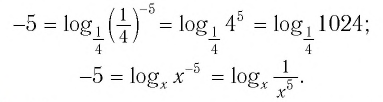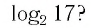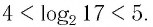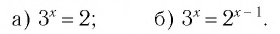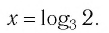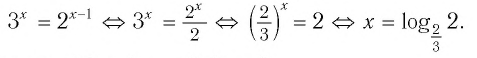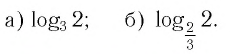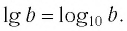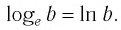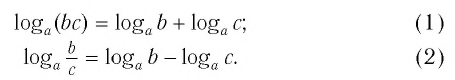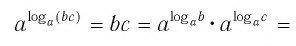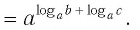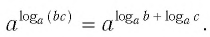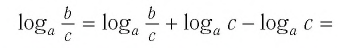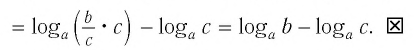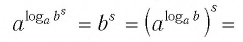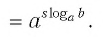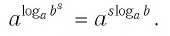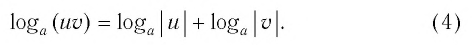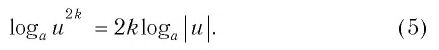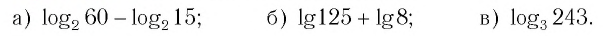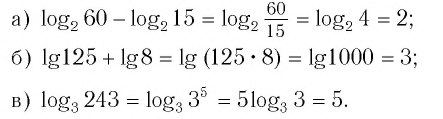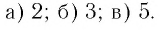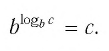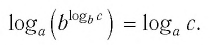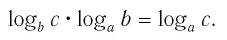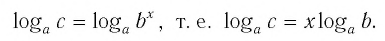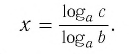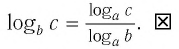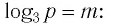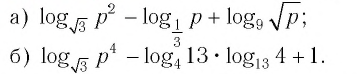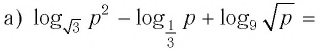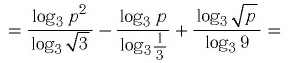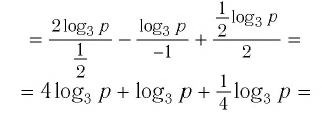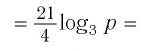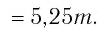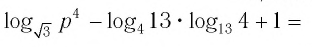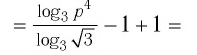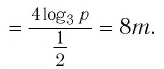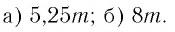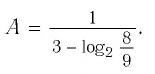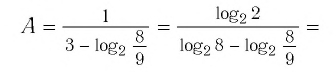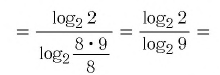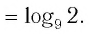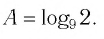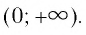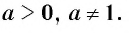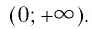//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
- Калькулятор онлайн. Решение логарифмических уравнений.
- Немного теории.
- Логарифмическая функция. Логарифмы
- Свойства логарифмов
- Десятичные и натуральные логарифмы
- Логарифмическая функция, её свойства и график
- Логарифмические уравнения
- Алгебра
- Уравнения вида logaf(x) = logag(x)
- Уравнения, требующие предварительных преобразований
- Логарифмические уравнения с заменой переменных
- Логарифмирование уравнений
- Переход от логарифмических неравенств к нелогарифмическим
- Логарифм — формулы, свойства и примеры с решением
- История логарифма
- Основные свойства логарифмов
- Пример №1
- Пример №2
- Пример №3
- Логарифмическая функция
- 🔍 Видео
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Калькулятор онлайн.
Решение логарифмических уравнений.
Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение. Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> ln(b) или log(b) или log(e,b) — натуральный логарифм числа b
log(10,b) — десятичный логарифм числа b
log(a,b) — логарифм b по основанию a
Введите логарифмическое уравнение
Решить уравнение
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Немного теории.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x 4 = 81
По определению арифметического корня имеем ( x = sqrt[4] = 3 )
Задача 2. Решить уравнение 3 x = 81
Запишем данное уравнение так: 3 x = 3 4 , откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3 x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение a x = b, где a > 0, ( a neq 1 ), b > 0, имеет единственный корень. Этот корень называют логарифмом числа b no основанию a и обозначают logab
Например, корнем уравнения 3 x = 81 является число 4, т.е. log381 = 4.
Определение. Логарифмом положительного числа b по основанию a, где a > 0, ( a neq 1 ), называется показатель степени, в которую надо возвести число a, чтобы получить b
log77 = 1, так как 7 1 = 7
Определение логарифма можно записать так:
Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.
Вычислить log64128
Обозначим log64128 = х. По определению логарифма 64 x = 128. Так как 64 = 2 6 , 128 = 2 7 , то 2 6x = 2 7 , откуда 6x = 7, х = 7/6.
Ответ log64128 = 7/6
Вычислить ( 3^ )
Используя свойства степени и основное логарифмическое тождество, находим
Решить уравнение log3(1-x) = 2
По определению логарифма 3 2 = 1 — x, откуда x = -8
Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, ( a neq 1 ), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log10b
Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо logeb
Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + frac + frac + frac + dots + frac + dots $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию.
Для этого используется формула замены основания логарифма:
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ log_a b = frac , ;; log_a b = frac $$
Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, ( a neq 1 )
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке ( (0; +infty) ), если a > 1,
и убывающей, если 0 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0 1.
Ось Oy является вертикальной асимптотой графика функции y = logax

Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Логарифмическая функция y = logax и показательная функция y = a x , где a > 0, ( a neq 1 ), взаимно обратны.
Видео:Алгебра 10 класс (Урок№27 - Логарифмические уравнения.)Скачать

Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х 2 + 4х + 3 = 8, т.е. х 2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого уравнения.
Ответ x = 1
Решить уравнение lg(2x 2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x 2 — 4x + 12) = lg(x 2 + 3x)
откуда
2x 2 — 4x + 12 = x 2 + 3x
x 2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Видео:Умножаем логарифмы В УМЕ🧠Скачать

Алгебра
Помощь студентам в решении контрольных и курсовых работ
Подготовка к дипломной, повышение уникальности
Помощь студентам в решении контрольных и курсовых работ
Консультация, сбор материала, повышение уникальности
Помощь в подготовке дипломной. Сопровождение до защиты!
План урока:
Задание. Укажите корень логарифмического уравнения
Задание. Решите урав-ние
В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид
Задание. Найдите решение логарифмического уравнения
Задание. Решите урав-ние
Задание. Решите урав-ние
Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:
Видео:Решение логарифмических уравнений #shortsСкачать

Уравнения вида logaf(x) = logag(x)
Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.
Задание. Решите урав-ние
Задание. Найдите корень урав-ния
Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид
С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.
Задание. Решите урав-ние
Получили квадратное уравнение, которое решаем с помощью дискриминанта:
Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:
Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:
Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Уравнения, требующие предварительных преобразований
Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x).
Задание. Решите урав-ние
с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:
Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:
Задание. Решите урав-ние
Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем
Задание. Решите урав-ние
Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать:
Задание. Решите урав-ние
Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что
Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что
Задание. Решите урав-ние
Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу
Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:
Видео:ЗАДАНИЕ 5 ЕГЭ (ПРОФИЛЬ). ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ.Скачать

Логарифмические уравнения с заменой переменных
Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.
Задание. Решите уравнение методом замены переменной
Задание. Найдите решение уравнения методом замены переменной
Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:
Видео:Интересная задача на логарифмы в ЕГЭСкачать

Логарифмирование уравнений
Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.
Задание. Укажите корни урав-ния
Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:
Возвращаемся от переменной t к переменной х:
Видео:Логарифм числа. Основное логарифмическое тождествоСкачать

Переход от логарифмических неравенств к нелогарифмическим
Рассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства
Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.
Задание. Найдите решение логарифмического неравенства
Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas:
Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение
Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:
Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).
Видео:Профильный ЕГЭ 2022. Логарифмические уравнения. Задание 1Скачать

Логарифм — формулы, свойства и примеры с решением
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 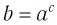
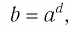
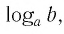
Таким образом, равенство 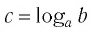
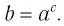
Определение:
Пусть 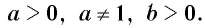
Приведем несколько примеров:
- а)
- б)
- в)
- г)
- д)
не имеет смысла, так как значение выражения
при любом значении х положительно и не может быть равно -9;
- е) по определению логарифма не имеют смысла и такие выражения, как
поскольку основанием логарифма должно быть положительное число, отличное от единицы.
Нахождение логарифма числа называется логарифмированием.
Обозначим 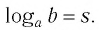
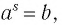
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 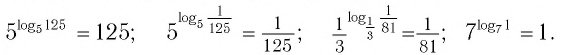
Например:
Видео:Как найти корень уравнения ЕГЭ 2021? Как решается 5 задание ЕГЭ по математике 2021 Часть 2Скачать

История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 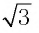
б) Записать число -5 в виде логарифмов по основанию 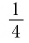
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 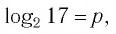
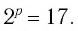
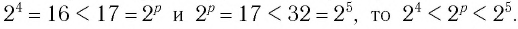
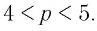
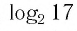
Ответ:
Пример:
Решение:
а) Поскольку 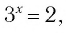
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 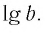
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Докажем утверждение (1).
По основному логарифмическому тождеству
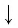
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 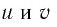
Следствие 2. При любом целом 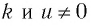
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 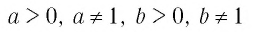
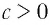
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 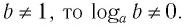
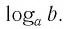
Способ 2. Пусть 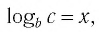
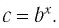
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




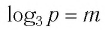
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
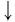
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Видео:Вычисление логарифмовСкачать

Логарифмическая функция
Рассмотрим выражение 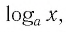
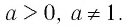
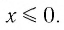
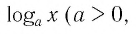
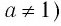
Определение:
Логарифмической функцией называется функция вида 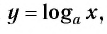
Область определения логарифмической функции — это естественная область определения выражения 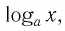
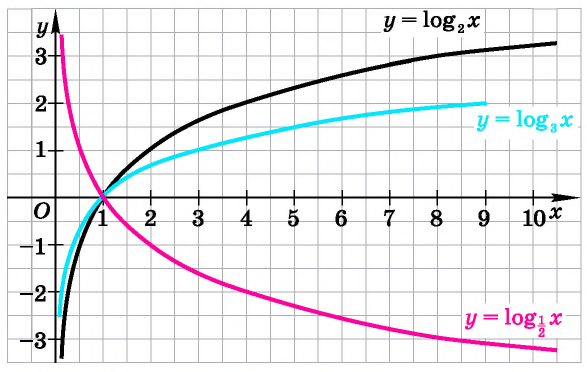
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 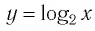
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 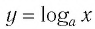
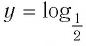
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 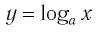
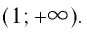
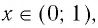
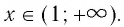
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Как решать 5 задание ЕГЭ по математике профиль Часть 3 / Репетитор по математике ЕГЭСкачать

Логарифм числа. 11 класс.Скачать
Логарифмы и логарифмические уравнения | Математика ЕГЭ 10 класс | УмскулСкачать

Область определения функции - 25 функций в одном видеоСкачать


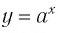
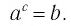
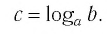
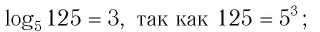
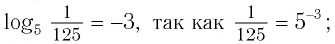
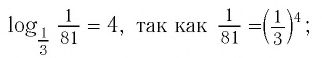
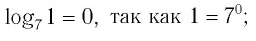
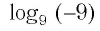 не имеет смысла, так как значение выражения
не имеет смысла, так как значение выражения 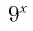 при любом значении х положительно и не может быть равно -9;
при любом значении х положительно и не может быть равно -9;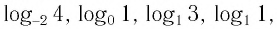 поскольку основанием логарифма должно быть положительное число, отличное от единицы.
поскольку основанием логарифма должно быть положительное число, отличное от единицы.