 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- Составьте уравнение, графиком которого является : а) пара прямых у = х + 1 и у = х — 1 ; б) парабола у = х ^ 2 и прямая у = — 2?
- Прямая пересекает координатные оси в точках А(5 ; 0) и В(0 ; — 2)?
- Запишите уравнение, графиком которого является множество точек плоскости, состоящие из :а) окружности с центром в точке К(2 ; 3) и радиусом 5, а также пары прямых, касающихся данной окружности и перпе?
- СОСТАВЬТЕ ТОЛЬКО УРАВНЕНИЕ ПРЯМОЙ?
- Укажите функцию графиком которой является парабола?
- Выпишите уравнения графиком которых являются прямые x ^ 2 — y ^ 2 = 1 x + y = 1?
- Какая фигура является графиком функции у = (х + а) ^ 2А) гиперболаБ) прямаяВ)параболаГ) кубическая парабола?
- Постройте прямую, являющуюся графиком уравнения — 2x + y = 3?
- Составьте линейное уравнение с двумя переменными графиком которой является прямая проходящая через начало координат и точку( — 3 ; 2)?
- Графиком какой функции является парабола, ветви которой направлены вверх?
- Напомните пожалуйста по графикам?
- Задания ОГЭ на анализ графиков Начало
- Изученные функции и их графики.
- Задания на соответствие графика и формулы функции.
- Линейная функция. Прямая линия.
- 📹 Видео
Видео:Функция прямой пропорциональности. 7 класс.Скачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Прямая пропорциональность и её график. Алгебра, 7 классСкачать

График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
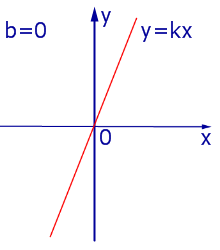 |
| Рис.1 |
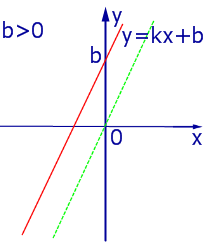 |
| Рис.2 |
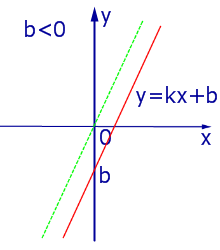 |
| Рис.3 |
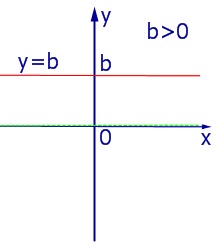
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
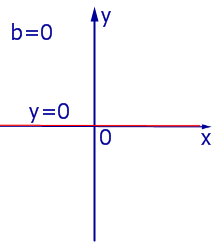 |
| Рис.4 |
 |
| Рис.5 |
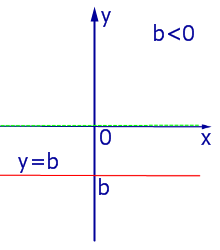 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:Уравнение прямой по графику. ПримерыСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:400 Алгебра 9 класс. Составьте уравнениеСкачать  Составьте уравнение, графиком которого является : а) пара прямых у = х + 1 и у = х — 1 ; б) парабола у = х ^ 2 и прямая у = — 2?Алгебра | 5 — 9 классы Составьте уравнение, графиком которого является : а) пара прямых у = х + 1 и у = х — 1 ; б) парабола у = х ^ 2 и прямая у = — 2. А) (y — x — 1)(y — x + 1) = 0 б) (y — x ^ 2)(y + 2) = 0. Видео:Линейная функция и её график. Алгебра, 7 классСкачать  Прямая пересекает координатные оси в точках А(5 ; 0) и В(0 ; — 2)?Прямая пересекает координатные оси в точках А(5 ; 0) и В(0 ; — 2). Напишите какое — нибудь линейное уравнение, графиком которого является эта прямая. Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Запишите уравнение, графиком которого является множество точек плоскости, состоящие из :а) окружности с центром в точке К(2 ; 3) и радиусом 5, а также пары прямых, касающихся данной окружности и перпе?Запишите уравнение, графиком которого является множество точек плоскости, состоящие из : а) окружности с центром в точке К(2 ; 3) и радиусом 5, а также пары прямых, касающихся данной окружности и перпендикулярных оси Ох б) параболы и прямой, проходящих через точки О (0 ; 0) и А(2 ; 2). Видео:ОГЭ 2022. Задание 11. Подробный разбор. Функция прямая. Как отличать.Скачать  СОСТАВЬТЕ ТОЛЬКО УРАВНЕНИЕ ПРЯМОЙ?СОСТАВЬТЕ ТОЛЬКО УРАВНЕНИЕ ПРЯМОЙ. Видео:Линейная функция и ее график. 7 класс.Скачать  Укажите функцию графиком которой является парабола?Укажите функцию графиком которой является парабола. Видео:Укажите неравенство, решением которого является любое число. | ОГЭ 2017 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРАСкачать  Выпишите уравнения графиком которых являются прямые x ^ 2 — y ^ 2 = 1 x + y = 1?Выпишите уравнения графиком которых являются прямые x ^ 2 — y ^ 2 = 1 x + y = 1. Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать  Какая фигура является графиком функции у = (х + а) ^ 2А) гиперболаБ) прямаяВ)параболаГ) кубическая парабола?Какая фигура является графиком функции у = (х + а) ^ 2 Г) кубическая парабола. Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать  Постройте прямую, являющуюся графиком уравнения — 2x + y = 3?Постройте прямую, являющуюся графиком уравнения — 2x + y = 3. Найдите по графику ординату точки, абцисса которой равна — 4. Видео:Как получить легкий балл на ОГЭ? / Подробный разбор заданий с графиками функций по математикеСкачать  Составьте линейное уравнение с двумя переменными графиком которой является прямая проходящая через начало координат и точку( — 3 ; 2)?Составьте линейное уравнение с двумя переменными графиком которой является прямая проходящая через начало координат и точку( — 3 ; 2). Видео:Решение графических задач на тему Газовые законыСкачать  Графиком какой функции является парабола, ветви которой направлены вверх?Графиком какой функции является парабола, ветви которой направлены вверх. Видео:Видеоурок "Канонические уравнения прямой"Скачать  Напомните пожалуйста по графикам?Напомните пожалуйста по графикам. Есть прямая, парабола, и гипербола. В каком то из них почти всегда функция с дробью, а в другом с квадратом. На этой странице находится вопрос Составьте уравнение, графиком которого является : а) пара прямых у = х + 1 и у = х — 1 ; б) парабола у = х ^ 2 и прямая у = — 2?. Здесь же – ответы на него, и похожие вопросы в категории Алгебра, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку. Видео:Алгебра 7 класс. 11 октября. Определяем функцию по графику еще разСкачать  Задания ОГЭ на анализ графиков |
| А | Б | В |
| 1 | 3 | 4 |
Ответы и решения некоторых задач временно скрыты. Это задачи для самостоятельного решения. Чтобы посмотреть ответы, воспользуйтесь соответствующими кнопками. Но предварительно попробуйте решить задачу самостоятельно.
Задача 2. Установите соответствие между функциями и их графиками.
На графике 1) линия с разрывом, следовательно в формуле есть (x) в знаменателе. Вывод: графику 1) соответствует формула А).
На графике 2) изображена прямая линия. Осталась только одна формула, где (x) в первой степени умножен на число (dfrac = dfraccdot x). Вывод: графику 2) соответствует формула В).
Два оставшихся графика нелинейны, т.е. кривые линии. Формула Б) представляет собой квадратный трёхчлен. Следовательно, график должен быть параболой. Мы знаем, что парабола симметрична относительно линии, проходящей через вершину. График 3) обладает этим свойством, а на графике 4) такую линию провести невозможно. Вывод: формула Б) соответствует графику 3).
Замечение. Проверку ответа можно сделать «по единичке», т.е. задать какое-либо значение (x), подставить его в формулы, вычислить значения (y) и найти соответствующие точки на графике. Но решить задание в буквальном смысле по единичке, т.е. подставить (x = 1) в формулу Б), а затем найти на графиках 3) и 4) ординаты точек с абсциссой 1, не получится. Потому что во всех случаях будет (y = 2). Выбор не состоится.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Задача 3. Установите соответствие между графиками функций и формулами, которые их задают.
Координатные плоскости здесь представлены без клеточек. Проверить принадлежность точек не получится, выбираем только по внешнему виду графиков.
Прямая линия олна – А). Её формула 1) содержит просто (x).
Симметричная кривая на графике В) – парабола. Формула 2) содержит (x^2).
На среднем графике кривая линия похожа на перевёрнутую половинку параболы. Это график функции 3) квадратный корень.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Видео:Функции и графики № 1-100 - Алгебра 9 класс МордковичСкачать

Линейная функция. Прямая линия.
Задача 4. Установите соответствие между графиками функций и формулами, которые их задают.
Все графики – прямые линии и все формулы имеют вид (y = kx + b). Выбираем по наклону к оси (Ox) и точке пересечения с осью (Oy).
На графике В) прямая никак не наклонена к оси (Ox), она ей параллельна. Следовательно, угол наклона равен 0, тангенс угла наклона равен 0, угловой коэффициент (k=0), и (y = kx + b = 0cdot x + b = 0 + b = b.) Таким образом, формула, которая задаёт прямую, параллельную оси абсцисс, не должна содержать (x). Здесь такая формула под номером 3.
В двух оставшихся графиках наклон на глаз кажется примерно одинаковым. Поэтому начнём с точки пересечения с с осью (Oy). Вспомним, что для точек, расположенных на этой оси, (x=0), поэтому (y = kx + b = kcdot0 + b = 0 + b = b.) Таким образом, высота точки пересечения графика с этой осью показывает значение коэффициента (b) в формуле функции. На первом графике пересечение при (y=2), подходит формула (2); y = x+2.) На втором – при (y=0), подходит формула (1); y = 2x,) так как (2x = 2x+0.)
Сделаем проверку по единичке для графиков А) и Б).
При (x=1) по формуле 2) получим (y = 1 + 2 = 3). Если мы правильно установили соответствие, то точка с координатами (1;3) должна лежать на графике А).
При (x=1) по формуле 1) получим (y = 2cdot1 =2). Если мы правильно установили соответствие, то точка с координатами (1;2) должна лежать на графике Б).
Отметим эти точки на указанных графиках. Точки «не промахнулись», значит задача решена верно.
Ответ:
| А | Б | В |
| 2 | 1 | 3 |
Итак, все графики, которые задаются формулой (y = b), т.е. формулой, содержащей (y) и число, но не содержащей (x), представляют собой прямые линии, параллельные оси (Ox). Все графики, которые задаются формулой (y = kx), т.е. формулой, содержащей (x) в виде одночлена первой степени, представляют собой прямые линии, проходящие через начало координат. Эти выводы нужно запомнить на будущее не только, чтобы быстрее решать это задание ОГЭ, но и для задания на графики во второй части экзаменационного варианта.
Задача 5. Установите соответствие между функциями и их графиками.
Прямые на графиках 1) и 2) имеют одинаковый наклон. Одинаковый угловой коэффициент (k = 2) мы видим в формулах Б) и В). Методом исключения делаем вывод, что для графика 3) остаётся формула А).
Теперь, чтобы установить соответствие между графиками 1) и 2) и формулами Б) и В) смотрим на точку пересечения с осью (Oy). На первом графике она находится ниже оси абсцисс, что говорит о том, что в формуле коэффициент (b) имеет отрицательное значение. Смотрим: (b = -6) в формуле Б). Вывод: формула Б) соответствует графику 1), тогда формула В) соответствует графику 2).
Проверка по единичке: [А); y = -2cdot1+6 = 4;;; Б); y = 2cdot1-6 = -4;;; В); y = 2cdot1+6 = 8]
Как и предполагалось, (y = 4) на графике 3), (y = -4) на графике 1) (y = 8) на графике 2).
Ответ:
| А | Б | В |
| 3 | 1 | 2 |
Задача 6. На рисунке изображены графики функций вида (y = kx+b.) Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
[1); -1;;; 2); -1,25;;; 3); 3;;; 4);0,8] В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Угловой коэффициент равен тангенсу угла наклона прямой к оси (Ox.) На данный момент мы знаем, что тангенс определён в прямоугольном треугольнике, как отношение противолежащего катета к прилежащему. Поэтому, прежде всего, надо начертить прямоугольные треугольники такие, что их гипотенузы лежат на заданных прямых, а катеты проходят по клеточкам. Вершины этих треугольников обязательно должны находиться в узлах клеточек, иначе будет трудно определить длины катетов. Размер треугольника может быть произвольным, «приклеить» его к прямой можно в любом удобном месте.
Угол наклона прямой по определению отсчитывается от положительного направления оси абсцисс (оси (Ox)), поэтому в наших треугольниках противолежащий катет всегда параллелен оси (Oy) (считаем клеточки по вертикали), а прилежащий – оси (Ox) (считаем клеточки по горизонтали).
Если прямая образует с положительным направлением оси абсцисс тупой угол, то угловой коэффициент будет со знаком минус. Поскольку линии клеток параллельны, то можно смотреть угол между прямой и правой частью горизонтальных линий сетки, как показано на рисунке.
Итак, вычисляем угловые коэффициенты по чертежу
[А); k = frac = 0,8; ;;; Б); k = -frac = -1,25; ;;; В); k = frac = 3; ;;; Г); k = -frac = -1 ] и сравниваем с предложенными значениями. [1);-1;;; 2);-1,25;;; 3); 3 ;;; 4);0,8.]
Ответ:
| А | Б | В | Г |
| 4 | 2 | 3 | 1 |
На эту тему также можно посмотреть видеоуроки на странице Линейная функция или на youtube-канале Mathematichka.
📹 Видео
401 Алгебра 9 класс. Составьте уравнениеСкачать


 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.












 Смотреть насколько близка вершина к центру координат здесь бесполезно, потому что не с чем сравнить. Остаётся только проверить по какой-нибудь точке. Легче всего по единичке.
Смотреть насколько близка вершина к центру координат здесь бесполезно, потому что не с чем сравнить. Остаётся только проверить по какой-нибудь точке. Легче всего по единичке. 








