Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Сборник практических и проверочных работ
для средних специальных учебных заведений
Сборник практических и проверочных работ разработан на основе Федерального государственного образовательного стандарта, утвержденного приказом Министерства образования и науки Российской Федерации № 282 от 06.04.2010, зарегистрирован Министерством юстиции рег. № 17241 от 17.05.2010г.
Сборник предназначен для преподавателей средних специальных учебных заведений и старших классов общеобразовательных школ для текущего контроля знаний
Каждое тестовое задание варианта имеет определенный порядковый номер, из которых — один верный и три неверных ответа. В каждом варианте теста 20 вопросов.
«отлично» — 90%-100% правильных ответов,
«хорошо»- 75%-89% правильных ответов,
«удовлетворительно»- 50%-74% правильных ответов,
«неудовлетворительно»- менее 50% правильных ответов.
Время, которое отводится на выполнение теста 30 минут.
1.Понятие множества является одним из основных:
а) Неопределяемых понятий математики б) Определяемых понятий математики
в) Устойчивых понятий математики г) Нет верного ответа
2. Множество N натуральных чисел:
а) Конечно б)Бесконечно в)Ограничено г)Симметрично
3. Множество всех букв греческого алфавита:
а) Бесконечно б)Конечно в)Пустое множество г)Ограничено
4. Если каждый элемент множества А является в то же время элементом множества В, то множество А называется:
а) Подмножеством Б б)Множество Б называется подмножеством множества А
в) Множество А не является подмножеством множества Б
г) Множество Б не является подмножеством множества А
5. Пересечением множеств А и В называется множество тех и только тех элементов, которые принадлежат:
а) Множеству А б) Множеству В
в) Множеству А и множеству В одновременно г)Нет верного ответа
6. Объединением множеств А и В называется множество тех и только тех элементов, которые входят:
а) Хотя бы в одно из множеств А и В
б) Которые состоит из тех и только тех элементов множества А, не принадлежащих множеству В
в) Которые состоит из тех и только тех элементов множества В, не принадлежащих множеству А
г) И в множество А и в множество В
7. Разностью двух множеств А и В называется множество, состоящее из тех и только тех элементов:
а) Множества А, которые не принадлежат множеству В
б) Множества В, которые не принадлежат множеству А
в) Множества элементов которые принадлежат множеству А и В одновременно
г) Нет верного ответа
8.Выберите утверждение о числовых множествах, которое является истинным…
а) Множество целых чисел является подмножеством множества действительных чисел.
б) Множество рациональных чисел является подмножеством множества иррациональных чисел.
в) Отрезок [1;2] является подмножеством промежутка (1;10].
г) Интервал (-4,0) является подмножеством отрезка [-3;-1].
9.Укажите пару (x ; y), находящуюся в отношении y = cos x :
10. Степень вершины А равна…
11.Даны множества: А=, В=
Количество элементов множества, являющегося пересечением множеств А и В, равно…
12. Даны два множества А и В
Область, выделенная серым цветом, является:
а) пересечением множества А и В б)дополнением множества В до множества А
в) объединением множества А и В г)разностью множества А и В
13. Какое из заданных отношений обладает свойством симметричности?
а) Отношение «быть меньше» б) Отношение «быть больше»
в) Отношение «перпендикулярности прямых» г)Отношение «быть делителем»
14. Количество ребер, идентичных вершине А,
равно
15. Выберите утверждение о числовых множествах, которое является истинным
а) Отрезок [1;10] является подмножеством промежутка (1;10]
б) Множество рациональных чисел является подмножеством множества иррациональных чисел
в) Множество целых чисел является подмножеством множества действительных чисел
г) Интервал (-4;0) является подмножеством множества целых чисел
16. Даны два множества А и В. Область, выделенная серым цветом является
а) пересечение множества А и В б)дополнение множества В до множества А
в) объединение множества А и В г)разность множества А и В
17. Укажите пустые множества среди следующих : множество целых корней уравнения х 2 -9=0; множество целых корней уравнения х 2 +9=0; множество действительных корней уравнения
а) множество целых корней уравнения х 2 -9=0
б) множество целых корней уравнения х 2 +9=0
в) множество целых корней уравнения х 2 -9=0;
г) множество целых корней уравнения х 2 +9=0;
д)множество действительных корней уравнения
18. Заданы множества А= и D=. Верным для них будет утверждение:
а) Множество А — подмножество множества D
б) Множество D — подмножество множества A
в) Множество А и множество D равны
г) Множество А — множество-степень множества D
19. Если отношение задано неравенством: 3x-4y
а) (0;1) б) (3;1) в) (2;0) г) (1;0)
20. Какое из множеств определяет А В , если А = , B =
Тема: Производная и ее приложения
ПРАКТИЧЕСКАЯ РАБОТА по теме « Вычисление пределов функций с использованием первого и второго замечательных пределов».
Вариант 1 Вариант 2 Вариант 3
1. lim 


2. lim 


3. lim 


4. lim 


5. lim 

6. lim 

7. lim 

8. lim 


9. lim 

10. lim 

11. lim 

12. lim 

ПРАКТИЧЕСКАЯ РАБОТА по теме «Нахождение производных по алгоритму. Вычисление производных сложных функций».
1. Найдите производную функций:
1) f ( x ) = ctg x +2 x 3 – 2 x , 2) f ( x ) = x 2 sinx , 3) f ( x ) = 
4) f(x) = (3x 2 – 2tgx) 5 , 5) f(x) = 


6) f(x)= 
2. Точка движется по закону S = 3t 3 – 12t +5.
Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3cosx+sinx в точке х0 = п.
1. Найдите производную функций:
1) f ( x ) = 



4) f(x) = x 2 tgx, 5) f(x) = 5cos x + x 5 – e x .
6) f(x)=x 3 +cos x. 7) f(x)=3 4x +x 2
2. Точка движется по закону S =2t 3 + t -5. Найдите скорость при t = 3с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = e x + lnx в точке х0 = 1.
1. Найдите производную функций:
1) f ( x ) = 


4) f(x) = x 7 ctgx, 5) f(x) = sin x — 2x 7 – 6 x .
6) f(x)=2x – sin x. 7) f(x)= 4e 5x – 7x 3
2. Точка движется по закону S = 5t 3 – 8t +3. Найдите скорость при t = 1с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3tgx- cosx в точке х0 = п.
1. Найдите производную функций:
1) f ( x ) = cos x +6 x 4 – 4 x ,
3) f(x) =
4) f(x) = (2x 3 – 5lnx) 3 ,
5) f(x) = 


7) f(x)=sin(x+x 3 ) — 
2. Точка движется по закону S = 2t 3 – 2t +5.
Найдите скорость движения при t = 3с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3log 2 x-5 в точке х0 = 3.
1. Найдите производную функций:
1) f ( x ) = 


2) f(x) = (5x – 4cosx) 5 ,
3) f(x) =
5) f(x) = 5sin x +x 6 – 8e x .
7) f ( x ) = — e x + 3 x 3 x
2. Точка движется по закону S = t 3 – 4t . Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3(x 3 +5) в точке х0 = 2.
1. Найдите производную функций:
1) f ( x ) = 
2) f(x) = (x 2 – e x ) 5 ,
3) f(x) = 

5) f(x) = 
7) f ( x )= x 4 + cos ( x +3 x 2 )
2. Точка движется по закону S = t 3 + 12t -5.
Найдите скорость движения при t = 2с.
3. Определите угловой коэффициент касательной, проведенной к кривой
у = 3/x в точке х0 = 3.
ТЕСТ по теме «Пределы и производные»
1. Предел отношения приращения функции в точке х к приращению аргумента, когда последнее стремится к нулю называется…
а) производной функции б) неопределенным интегралом
в) пределом функции г) первообразной
2. Если материальная точка движется по закону S(t), то первая производная от пути по времени есть…
а) угловой коэффициент б) ускорение движения
в) скорость в данный момент времени г) нет верного ответа
3. Геометрический смысл производной состоит в том, что …
а) она равна пределу функции б) она равна всегда нулю
в) она равна угловому коэффициенту касательной
г) она равна максимальному значению функции
4. Дифференцирование – это…
а) вычисление предела б) вычисление приращения функции в) нахождение производной от данной функции г) составление уравнения нормали
5. Эта формула выражает
а) первый замечательный предел; б) первообразную
в) угловой коэффициент касательной г) максимальному значению функции
6. Уравнение касательной к данной линии в точке М имеет вид…
в) y — y0 = х — х0 г) y = y • х
7. Производная постоянной величины равна…
а) единице б) самой постоянной в) не существует г) нулю
8. При вычислении производной постоянный множитель можно…
а) возводить в квадрат б) выносить за знак производной
в) не принимать во внимание г) принять за нуль
9. Ускорение прямолинейного движения равно…
а) скорости от пути по времени б) первой производной от пути по времени
в) второй производной от пути по времени г) нулю
10. Функция возрастает на заданном промежутке, если…
а) первая производная положительна б) вторая производная положительна
в) первая производная отрицательна г) первая производная равна нулю
11. Найти:
а) не существует б) 0; в)
12. Найти
а) 1; б) 0; в) -1; г)
13. Найти
а) не существует; б) 0 ; в) 
14. Найти:
а) е 2 ; б) е ; в) 1 ; г)
15. Найдите производную функции y = x 3 + cosx.
а ) y / = 3x 2 – sin x б ) y / = x 3 – sin x в ) y / = 3x 2 + sin x г ) y / = x 3 ln3 + sin x
16. Найдите производную функции y = 2x – sin x.
а ) y / = x 2 – cos x б ) y / = x 2 – sin x в )y / = 2 — cos x г ) y / = 1 + cos x
17.. Найдите производную функции y = 2 x + 1.
а) y / = 


18. Найдите производную функции y = — e x + 3x 3 .
а ) y / = e x + 3x б ) y / = -xe x + 9x 2 в ) y / = -e x + 9x 2 г ) y / = -e x-1 + 9x 3 .
19. Найдите производную функции y = e 2x – ln (3x – 5)
а ) y / = 2e 2x — 

г) y / = e 2x —
20. Вторая производная 
а) y // = 4; б) y // = 8 ; в) y // = 6 ; г) y // = 7
Тема: Интеграл и его применение
ПРАКТИЧЕСКАЯ РАБОТА по теме «Интегрирование простейших функций. Вычисление простейших определенных интегралов».
Вариант 1 Вариант 2
1).
1).
2).
2).
3).
3)
4).
4).
5).
5).
6).
6)
7).
7).
ПРАКТИЧЕСКАЯ РАБОТА по теме «Решение прикладных задач».
1. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной
2. Найти объем тела, полученного при вращении вокруг оси абсцисс
криволинейной трапеции, ограниченной линиями: y = x 2 , y = 0, x = 1, x = 4 .
3. Скорость движения точки изменяется по закону V ( t )= 2 t 3 -3 t 2 +6 t (м/с). Найти путь, пройденный телом за 2 сек
1. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной
линиями : y= -x 2 + 1, y=0, x=1
2. Найти объем тела, полученного при вращении вокруг оси абсцисс
криволинейной трапеции, ограниченной линиями: у=2х 2 y = 0, x = 0, x = 1.
3. Скорость движения точки изменяется по закону V ( t )= t 3 + t 2 + t (м/с). Найти путь S, пройденный точкой за четвертую секунду.
ТЕСТ по теме «Интеграл»
1.Функция F называется первообразной для функции f на некотором промежутке, если для всех x из этого промежутка существует производная F / (х), равная f(х), т.е. F / (х)=f(х) это…
а) формула Ньютона-Лейбница б) дифференциал функции
в) первообразная для функции f г) производная в точке
2. Множество первообразных для данной функции f(х) называется…
а) функцией б) неопределенным интегралом
в) постоянным множителем г) частной производной
3. Операция нахождения неопределенного интеграла называется…
а) дифференцированием функции б) преобразованием функции
в) интегрированием функции г) нет верного ответа
4. Непосредственное интегрирование, метод подстановки, интегрирование по частям это…
а) методы нахождения производной б) методы интегрирования
в) методы решения задачи Коши г) все ответы верны
5. Производная от неопределенного интеграла равна…
а) подынтегральной функции б) постоянной интегрирования
в) переменной интегрирования г) любой функции
6. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен…
а) произведению интегралов этих функций б) разности этих функций
в) алгебраической сумме их интегралов г) интегралу частного этих функций
7. Определенный интеграл вычисляют по формуле…
а ) 



в) 

8. Определенный интеграл с одинаковыми пределами равен…
а) единице б) бесконечности в) нулю г) указанному пределу
9. При перемене местами верхнего и нижнего пределов интегрирования определенный интеграл…
а) остается прежним б) меняет знак
в) увеличивается в два раза г) равен нулю
10. Определенный интеграл используется при вычислении…
а) площадей плоских фигур б) объемов тел вращения
в) пройденного пути г) всех перечисленных элементов
11. Формула Ньютона-Лейбница
а) 
в) 
12. Вычисление пути, пройденного материальной точкой производится по формуле:
а) 


13. Если криволинейная трапеция, ограниченная линией 
а) 


14. Если 
а) 


15. Укажите первообразную функции
а) 


16.Определенный интеграл 
17.Площадь криволинейной трапеции, ограниченной линиями y = 4 – x 2 , y = 0 определяется интегралом
а) 


18. В результате подстановки t = 3x + 2 интеграл 
а) 


19.Определенный интеграл 
а)19; б)18 ; в)35; г) 27
20. Множество всех первообразных функции y = 5 
а) 


ПРОВЕРОЧНАЯ РАБОТА по теме «Неопределенный интеграл. Непосредственное интегрирование. Замена переменной».
1. Найти неопределенные интегралы методом непосредственного интегрирования
а). 
в) 
б). 

г)
2. Найти неопределенные интегралы методом подстановки

3.Найти неопределенный интеграл методом интегрирования по частям: 
1. Найти неопределенные интегралы методом непосредственного интегрирования
1. 
2. 
3. 
4. 
5. 
2. Найти неопределенные интегралы методом подстановки .
2. 
3.Найти неопределенный интеграл методом интегрирования по частям: 
ПРОВЕРОЧНАЯ РАБОТА по теме «Определенный интеграл. Геометрический смысл определенного интеграла».
1. Вычислить определенный интеграл: 
2. Вычислить определенный интеграл методом подстановки: 
3.Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: 
4.Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: 
5.Скорость движения точки изменяется по закону 
Вычислить определенный интеграл: 
Вычислить определенный интеграл методом подстановки: 
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: 
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: 
Скорость движения точки изменяется по закону 
Тема: Обыкновенные дифференциальные уравнения
Решить дифференциальные уравнения и найти частные решения.
Индивидуальное задание по порядковому номеру в журнале, т.е. в задании вместо N студент подставляет свой порядковый номер.
Решить дифференциальные уравнения .
1. Уравнение, связывающее переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции) называется
1. Дифференциальным 2. Интегральным 3.Логарифмическим 4 Показательным
2. Общим решением дифференциального уравнения первого порядка называется функция:
1. 


3. Частным решением уравнения 



4. Если дифференциальное уравнение содержит производную или дифференциал не выше второго порядка, то оно называется:
1. Дифференциальным уравнением второго порядка
2. Дифференциальным уравнением первого порядка
3. Дифференциальным уравнением третьего порядка
4. Нет верного ответа
5. Общим решением дифференциального уравнения второго порядка называется функция:



4. 
6 . Характеристическое уравнение дифференциального 
1. -5k+6=0 2. k 2 -5k+6=0 3. k+6=0 4. k 2 -5k=0
7. Метод решения данного уравнения g(y)dy+f(x)dx=0 …
1. метод разделения переменных 2. метод с постоянными коэффициентами;
3. метод параметров; 4. метод составления характеристического уравнения
8. Дифференциальное уравнение 
а) 


9.Общим решением дифференциального уравнения называется …
интеграл, содержащий произвольную постоянную С
интеграл ,содержащий конкретное значение С
значение определенного интеграла
интегральная линия дифференциального уравнения
10. Степенью дифференциального уравнения называется
показатель степени производной искомой функции, с которым эта производная входит в данное уравнение
наибольшая степень выражения;
сумма показателей производных;
сумма показателей выражения
11. Частным решением дифференциального уравнения называется …
интеграл, содержащий конкретное значение С
интеграл, содержащий произвольную постоянную С
значение определенного интеграла
интегральная линия дифференциального уравнения
12. Для нахождения частного решения дифференциального уравнения, необходимо
знание начальных условий;
знание пределов интегрирования
знание методов решения дифференциальных уравнений
знание методов интегрирования
13. Дифференциальное уравнение вида Y / +P(x)=Q(X) называется …
1.линейным 2. квадратным 3. параметрическим 4. уравнением с одной переменной
14. Уравнение вида Y // +PY / +QY=F(x) называется …
1. линейным уравнением второго порядка с постоянными коэффициентами
2. параметрическим уравнением второго порядка с постоянными коэффициентами
3. однородным уравнением второго порядка
4. биквадратным уравнением
15. Общий вид решения уравнения Y // +PY / +QY=0 при условии к1, к2 – действительные корни характеристического уравнения…
16. Дифференциальное уравнение 
1) 


17. Характеристическое уравнение дифференциального 
1) k 2 -6k+13=0 2) k 2 -6k=0 3) k 2 +13=0 4) 6k+13=0
18. Уравнение вида 
1) неоднородным 2) однородным 3) параметрическим 4) уравнением с одной переменной
19. Дифференциальные уравнения второго порядка решаются методом
1) однократного интегрирования
2) двукратным интегрированием
3) однократным дифференцированием
4) двукратным дифференцированием
20. Характеристическое уравнение дифференциального 
1) 


Тема « Элементы комбинаторики, случайная величина, её вероятность и математическое ожидание.
ПРАКТИЧЕСКАЯ РАБОТА по теме «Элементы комбинаторики»
а) 
2.Из урны, в которой находятся 5 белых и 4 черных шара, вынимают один шар. Найти вероятность того, что шар черный.
3. В ячейке содержится 10 одинаковых деталей помеченных номерами 1,2,3,…,10. наудачу извлечены 6-ть деталей. Найти вероятность того, что среди извлеченных деталей останется деталь № 1
а) 
2. В лотерее из 10 000 билетов имеются 2 000 выигрышных. Вынимают наугад один билет. Чему равна вероятность тому, что билет выигрышный.
3. В ящике содержится 10 одинаковых деталей помеченных номерами 1,2,3,…10. научу извлечены 6-сть деталей. Найти вероятность того, что среди извлеченных деталей останется деталь № 1 и №2.
1. Выписать значения выражений:
А) 5!+6!; Б)
2. В ящике 12 белых и 17 черных шаров. Извлекают на удачу один шар. Найти вероятность того, что вынутый шар окажется белым.
3.В коробке 5 одинаковых деталей, 3-и из них окрашены, на удачу извлекли 2-а изделия. Найти вероятность того, что среди извлеченных изделий окажется одно окрашенное изделие.
А) 
2. Пусть имеется 80 деталей, среди которых 60 исправленных, а 20 бракованных. Найти вероятность того, что взята наугад деталь окажется исправной.
3. В коробке 5 одинаковых деталей, 3-и из них окрашены, на удачу извлекли 2-а изделия. Найти вероятность того, что среди извлеченных изделий окажется одно окрашенное изделия.
1. Вычислить: А) 
2. Телефонный номер состоит из шести цифр. Найдите вероятность, что все цифры различные.
3. В группе 14 студентов, из которых 10 отличников. По списку наудачу отбирают 8 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5-ть отличников.
1. Вычислить: А) 
2. Среди 180 деталей, изготовленных на станке, оказалось 10 деталей, не отвечающих стандарту. Найти вероятность выбора детали, не отвечающих стандарту.
3. В цехе работают 6 мужчин и 4 женщины. По табельным номерам на удачу отобрали 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3-и женщины.
ПРОВЕРОЧНАЯ РАБОТА по теме « Случайная величина. Вероятность»
Из корзины, в которой находятся 4 белых и 7 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Определить вероятность появления «герба» при бросании монеты.
В корзине 20 шаров: 5 синих, 4 красных, остальные черные. Выбирают наудачу один шар. Определить, с какой вероятностью он будет цветным.
1. В одной корзине находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
2. Бросают две монеты. Определить, с какой вероятностью появится «герб» на обеих монетах.
3. Из корзины, в которой находятся 7 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется белым.
ПРОВЕРОЧНАЯ РАБОТА по теме « Математическое ожидание и дисперсия случайной величины».
В лотерее 100 билетов. Разыгрывается один выигрыш в 200 рублей и двадцать выигрышей по 50 рублей. Пусть Х – величина возможного выигрыша для человека, имеющего один билет. Составить закон распределения этой случайной величины Х.
Случайная величина Х задана законом распределения:
3. Найти ее математическое ожидание.
Согласно статистике, вероятность того, что двадцатипятилетний человек проживет еще год, равно 0,992. Компания предлагает застраховать жизнь на год на 1000 у.е. с уплатой 10 у.е. взноса. Определить, какую прибыль ожидает компания от страховки одного двадцатипятилетнего человека.
Случайная величина Х задана законом распределения:
6.Найти дисперсию и среднее квадратичное отклонение этой случайной величины Х.
7.Случайные величины X и Y заданы законом распределения. Найти математическое ожидание этих случайных величин и определить по таблицам, какая из данных величин более рассеяна. Подсчитать дисперсии D(X) и D(Y). Убедиться, что D(X)>D(Y).
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Назовите пустые множества: а) множество корней уравнения 0 • х = 1; б) множество корней уравнения x : 1 = 0; в) множество натуральных чисел, меньших
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Ваш ответ
Видео:Множество. Элементы множества. 5 класс.Скачать

решение вопроса
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Похожие вопросы
- Все категории
- экономические 43,407
- гуманитарные 33,633
- юридические 17,905
- школьный раздел 608,009
- разное 16,855
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№ 801-900 - Алгебра 8 класс МакарычевСкачать

Выберите утверждение о числовых множествах, которое является истинным
а) Отрезок [1;10] является подмножеством промежутка (1;10]
б) Множество рациональных чисел является подмножеством множества иррациональных чисел
в) Множество целых чисел является подмножеством множества действительных чисел
г) Интервал (-4;0) является подмножеством множества целых чисел
Даны два множества А и В
Область, выделенная серым цветом является
а) пересечение множества А и В
б) дополнение множества В до множества А
в) объединение множества А и В
г) разность множества А и В
17. Укажите пустые множества среди следующих : множество целых корней уравнения х 2 -9=0; множество целых корней уравнения х 2 +9=0; множество действительных корней уравнения
а) множество целых корней уравнения х 2 -9=0
б) множество целых корней уравнения х 2 +9=0
в) множество целых корней уравнения х 2 -9=0; множество целых корней уравнения х 2 +9=0;
г) множество целых корней уравнения х 2 +9=0; множество действительных корней уравнения
18. Заданы множества А= и D=. Верным для них будет утверждение:
а) Множество А — подмножество множества D
б) Множество D — подмножество множества A
в) Множество А и множество D равны
г) Множество А — множество-степень множества D
19. Если отношение задано неравенством: 3x-4y
Пример: 1) F(x)=sin x – первообр. F(x)=cosx , т.к.
2) 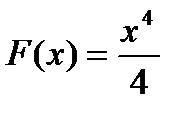


Неопределенный 
Опр. Интегрирование – это процесс нахождения первообразованых
Опр. Множество первообразных для данной функции f(x) над неопределенным интегралом и обозначается
Пр.
Таблица неопределенных интегралов
1. 
2. 
3. 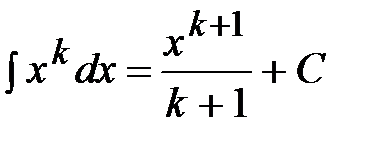

4. 
5. 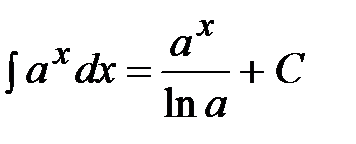

6. 
7. 
8. 
9. 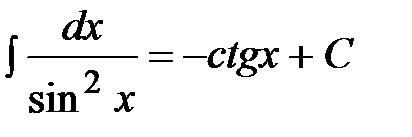
10. 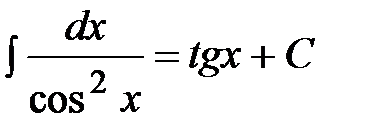
11. 
12. 
13. 
14.
Свойства неопределенного интеграла:
- Если
– постоянная величина, то
.
.
.
.
💡 Видео
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Рациональные и иррациональные числа за 5 минутСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

ОГЭ по математике. Решаем уравнения | МатематикаСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Что такое математическая последовательность? | Математика | TutorOnlineСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Деление многочлена на многочлен. 10 класс.Скачать

Арифметическая прогрессия 9 класс. Формулы, о которых вы не знали | МатематикаСкачать

Разбор 6 задания с параметром А для ОГЭ по информатике 2023 | УмскулСкачать

Множества и операции над множествамиСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать



























































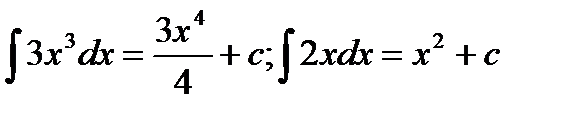

 – постоянная величина, то
– постоянная величина, то 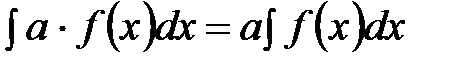 .
.
 .
. .
. .
.