Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:
ax 2 + bx + c = 0 — квадратное уравнение,
где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
| x 2 + | b | x + | c | = 0. |
| a | a |
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x 2 + px + q = 0.
Уравнение x 2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
является приведённым, а уравнение:
можно заменить приведённым уравнением, разделив все его члены на -3:
Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax 2 + bx + c = 0 |  | ||||
| ax 2 + 2kx + c = 0 |  | ||||
| x 2 + px + q = 0 |
|
Обратите внимание на уравнение:
это преобразованное уравнение ax 2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Пример 1. Решить уравнение:
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Ответ: — | 1 | , -2. |
| 3 |
Определим, чему равны коэффициенты:
Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
Приведём уравнение к общему виду:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
Определим, чему равны коэффициенты:
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Неполные квадратные уравнения
О чем эта статья:
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
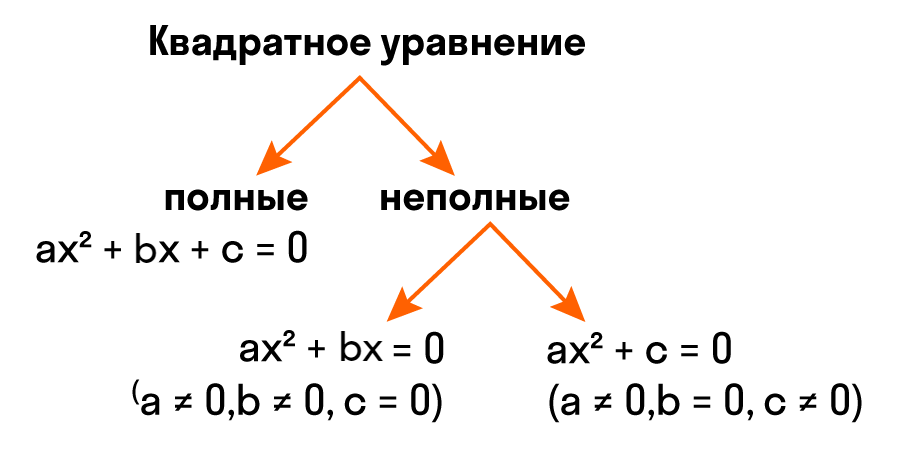
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трех видов:
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
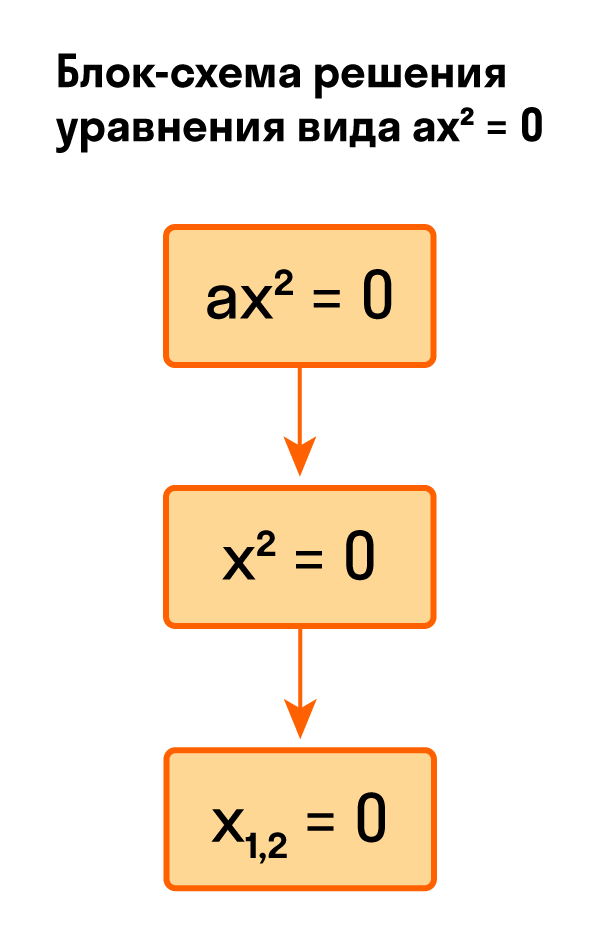
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Видео:Метод выделения полного квадрата. 8 класс.Скачать  Как решить уравнение ax² = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0.
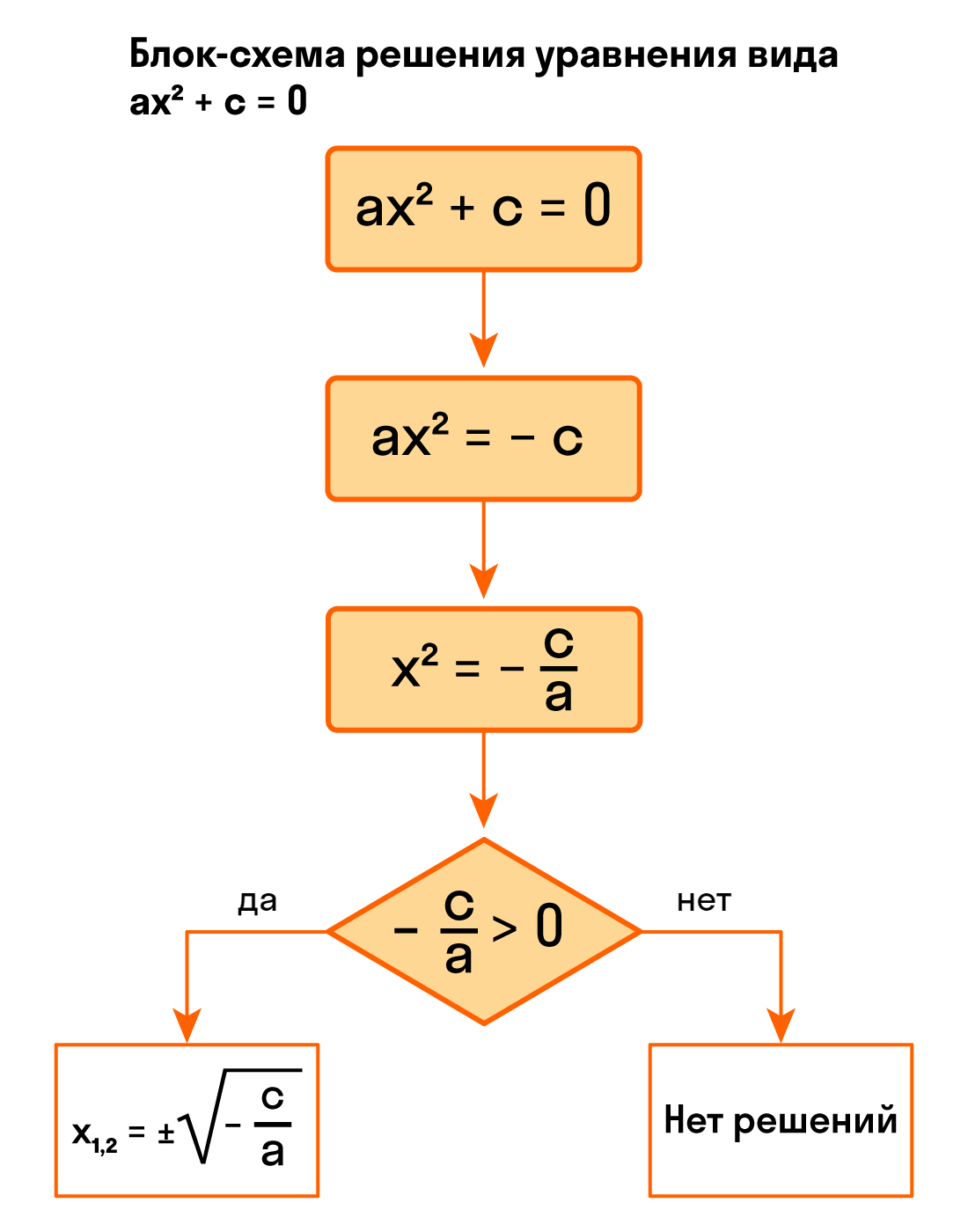
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса! Видео:Теорема Виета. 8 класс.Скачать  Как решить уравнение ax² + с = 0Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Разделим обе части на 9: Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0.
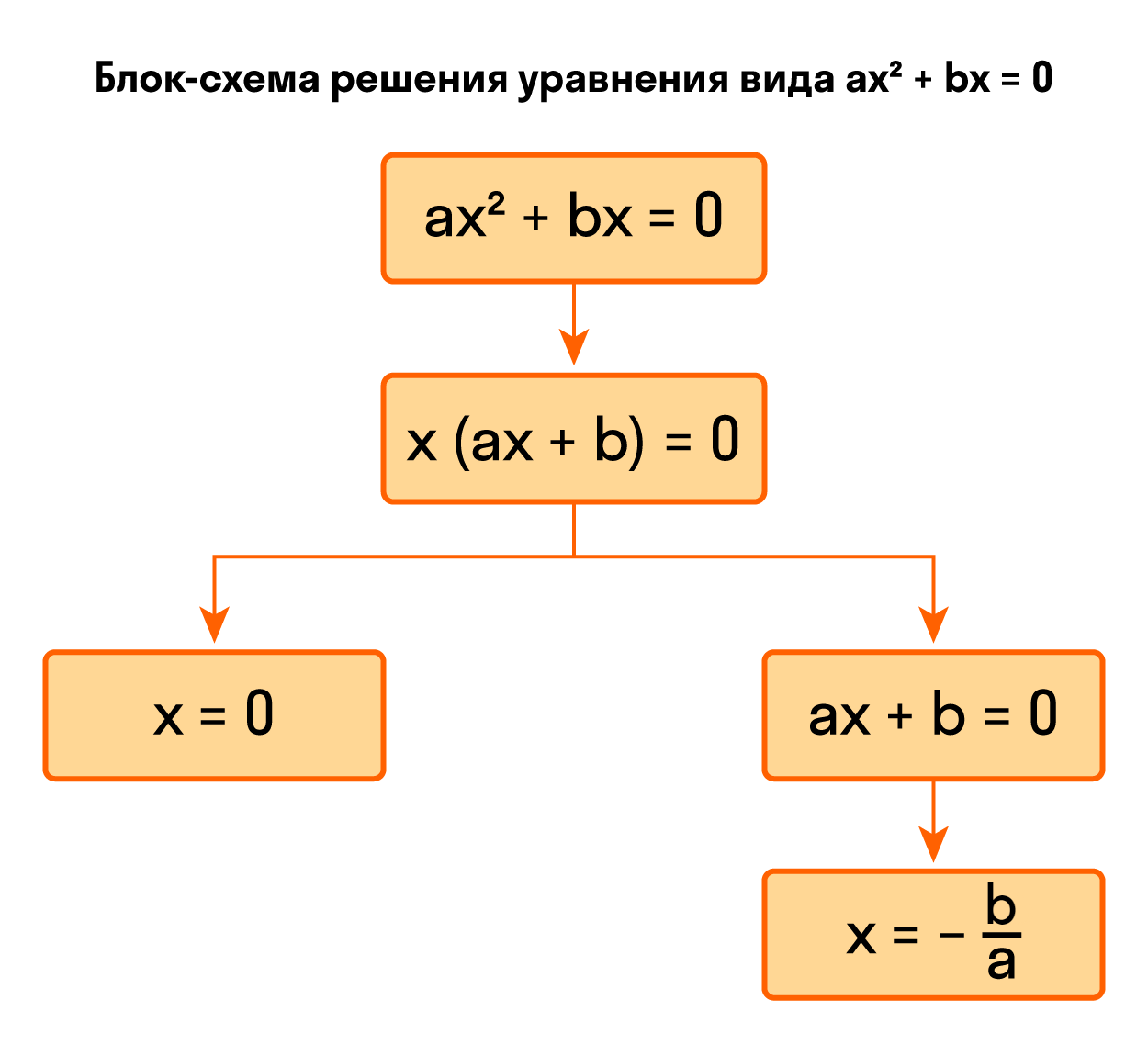
Разделим обе части на -1: Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать  Как решить уравнение ax² + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0
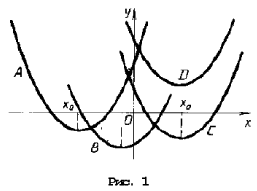
Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Разложить левую часть уравнения на множители и найти корни: Ответ: х = 0 и х = 4. Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке. Видео:Алгебра 8 класс (Урок№30 - Решение приведённых квадратных уравнений. Теорема Виета.)Скачать  Квадратные трехчлены и параметрыЗадачи с параметрами относятся к наиболее трудным заданиям, предлагаемым на вступительных экзаменах. Это связано с тем, что они требуют хорошего понимания «глубинных» свойств функций, и их решение носит творческий характер. Однако знание некоторых простых правил и алгоритмов решения необходимо. Вводные замечания и простейшие примеры Пример 1. При каких значениях a уравнение ax 2 + 2x + 1 = 0 имеет два различных корня? Решение. Данное уравнение является квадратным относительно переменной x при a № 0 и имеет различные корни, когда его дискриминант т. е. при a Кроме того, при a = 0 получается уравнение 2x + 1 = 0, имеющее один корень. Таким образом, a О (– Ґ ; 0) И (0; 1). Правило 1. Если коэффициент при x 2 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль. Пример 2. Уравнение ax 2 + 8x + c = 0 имеет единственный корень, равный 1. Чему равны a и c? Решение. Начнем решение задачи с особого случая a = 0, уравнение имеет вид 8x + c = 0. Это линейное уравнение имеет решение x0 = 1 при c = – 8. При a № 0 квадратное уравнение имеет единственный корень, если Кроме того, подставив корень x0 = 1 в уравнение, получим a + 8 + c = 0. Решая систему двух линейных уравнений, найдем a = c = – 4. Теорема 1. Для приведенного квадратного трехчлена y = x 2 + px + q (при условии p 2 і 4q) Теорема 2. Для квадратного трехчлена y = ax 2 + bx + c с двумя корнями x1 и x2 имеет место Замечание. Часто про квадратные уравнения с дискриминантом, равным нулю и имеющим, соответственно, один корень, говорят, что оно имеет два совпадающих корня (?). Это связано с разложением многочлена на множители, приведенным в теореме 2. (Правильно говорить и понимать в этом случае нужно «один корень кратности два». – Прим. ред.) Будем обращать внимание на эту тонкость и выделять случай единственного корня кратности 2. Пример 3. В уравнении x 2 + ax + 12 = 0 определить a таким образом, чтобы разность корней уравнения равнялась единице. Решение. Разность корней Пример 4. При каких a сумма квадратов корней уравнения 2x 2 + 4x + a = 0 равна 6? Решение. Запишем уравнение в виде Пример 5. При всех a решить уравнение ax 2 – 2x + 4 = 0. Решение. Если a = 0, то x = 2. Если a № 0, то уравнение становится квадратным. Его дискриминант Расположение корней квадратного трехчлена Графиком квадратного уравнения является парабола, а решениями квадратного уравнения – абсциссы точек пересечения этой параболы с осью Ox. Основой решения всех задач этого параграфа является изучение особенностей расположения парабол с заданными свойствами на координатной плоскости. Пример 6. При каких a корни уравнения x 2 – 2ax + a 2 – a – 6 = 0 имеют разные знаки? Решение (рис. 1). Квадратное уравнение либо не имеет решений (график – парабола вида D), либо имеет один или два положительных корня (парабола C), либо имеет один иди два отрицательных корня (парабола A), либо имеет корни разных знаков (парабола B). Легко сообразить, что последний тип парабол, в отличие от прочих, характеризуется тем, что f(0) 2 – a – 6 Данное решение допускает обобщение, которое мы сформулируем как следующее правило. Правило 2. Для того чтобы уравнение ax 2 + bx + c = 0 имело два разных корня x1 и x2 таких, что x1 Пример 7. При каких a уравнение x 2 – 2ax + a 2 – a – 6 = 0 имеет два разных корня одного знака? Решение. Нас интересуют параболы типа A и C (см. рис. 1). Они характеризуются тем, что откуда a О (– 6; – 2) И (3; + Ґ ). Пример 8. При каких a уравнение x 2 – 2ax + a 2 – a – 6 = 0 имеет два разных положительных корня? Решение. Нас интересуют параболы типа C на рис. 1. Чтобы уравнение имело корни, потребуем Так как оба корня уравнения по условию должны быть положительными, то и абсцисса вершины параболы, лежащая между корнями, положительна: x0 = a > 0. Ордината вершины f(x0) 0, то в силу непрерывности исследуемой функции найдется точка x1 О (0; x0) такая, что f(x1) = 0. Очевидно, что это меньший корень уравнения. Итак, f(0) = a 2 – a – 6 > 0, и, собирая все условия вместе, получим систему с решением a О (3; + Ґ ). Пример 9. При каких a уравнение x 2 – 2ax + a 2 – a – 6 имеет два разных отрицательных корня? Решение. Изучив параболы типа A на рис. 1, получим систему откуда a О (– 6; – 2). Обобщим решение предыдущих задач в виде следующего правила. Правило 3. Для того чтобы уравнение ax 2 + bx + c = 0 имело два разных корня x1 и x2, каждый из которых больше (меньше) M, необходимо и достаточно, чтобы Пример 10. Функция f(x) задается формулой Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение. Решение. Все возможные решения данного уравнения получаются как решения квадратного уравнения
с дополнительным условием, что хотя бы один (очевидно, больший) корень x2 і a. Естественно, чтобы уравнение имело корни, должно быть Графиком левой части выделенного уравнения является парабола, абсцисса вершины которой равна x0 = 2a + 7. Решение задачи дают два типа парабол (рис. 2). A: x0 і a, откуда a і – 7. В этом случае больший корень многочлена x2 і x0 і a. B: x0 Ј 0, откуда Окончательно Три решения одного неравенства Пример 11. Найти все значения параметра a, при которых неравенство x 2 – 2ax + a 2 + 2a – 3 > 0 выполняется: 1) при всех значениях x; Решение. Первый способ. 1) Очевидно данное неравенство выполняется при всех x, когда дискриминант отрицателен, т. е.
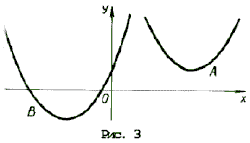
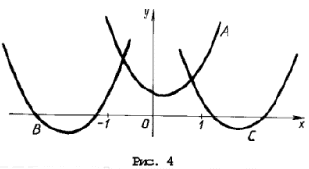
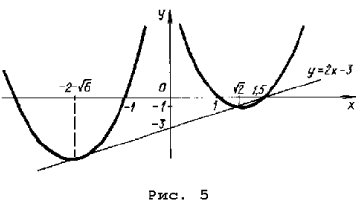
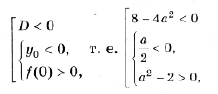
откуда a > 2) Чтобы лучше понять то, что требуется в условии задачи, применим простой прием: на координатной плоскости нарисуем какие-нибудь параболы, а потом возьмем и закроем левую относительно оси Oy полуплоскость. Та часть параболы, которая останется видимой, должна быть выше оси Ox. Условие задачи выполняется в двух случаях (см. рис. 3): A: график функции y = x 2 – 2ax + a 2 + 2a – 3 лежит выше оси Ox, т. е. D B: оба корня (может быть, один, но двукратный) уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся левее начала координат. По правилу 3 это условие эквивалентно системе неравенств D і 0, x0 Ј 0 и f(0) і 0. Однако при решении данной системы первое неравенство можно опустить, так как если даже какое-то значение a не удовлетворяет условию D і 0, то оно автоматически попадает в решение пункта A. Таким образом, решаем систему откуда a Ј – 3. Объединяя решения пунктов A и B, получим ответ: 3) Условие задачи выполняется в трех случаях (см. рис. 4): A: график функции y = x 2 – 2ax + a 2 + 2a – 3 лежит выше оси Ox, т. е. D B: оба корня (может быть, один кратности 2) уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся левее – 1. Это условие эквивалентно, как мы знаем из правила 3, системе неравенств D і 0, x0 0; C: оба корня уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся правее 1. Однако в пунктах B и C, также как и в решении предыдущей задачи, неравенство, связанное с дискриминантом, можно опустить. Соответственно получаем две системы неравенств Рассмотрев все случаи, получим результат: a > Второй способ. Для того чтобы выполнялось условие каждого из трех пунктов задачи, наименьшее значение функции 1) Вершина параболы y = x 2 – 2ax + a 2 + 2a – 3 находится в точке (a; 2a – 3), поэтому наименьшее значение функции на всей числовой прямой равно 2a – 3, и a > 2) на полуоси x і 0 наименьшее значение функции равно f(0) = a 2 + 2a – 3, если a і 0. Разбирая оба случая, получим 3) Наименьшее на отрезке [– 1; 1] значение функции равно Поскольку наименьшее значение должно быть положительно, получаем системы неравенств Решение этих трех систем – множество Третий способ. 1) Вершина параболы y = x 2 – 2ax + a 2 + 2a – 3 находится в точке (a; 2a – 3). Нарисуем на координатной плоскости множество, которое образуют вершины всех парабол при различных a (рис. 5). Это – прямая y = 2x – 3. Напомним, что каждой точке этой прямой соответствует свое значение параметра, и из каждой точки этой прямой «выходит» парабола, соответствующая данному значению параметра. Параболы, целиком находящиеся над осью Ox, характеризуются условием 2a – 3 > 0. 2) Решениями этого пункта являются все решения первого пункта, и, кроме того, параболы, для которых a – отрицательны, и f(0) = a 2 + 2a – 3 і 0. 3) Из рис. 5 видно, что нас интересуют параболы, для которых либо a отрицательно и f(– 1) = a 2 + 4a – 2 > 0, Уравнения и неравенства, сводящиеся к квадратным Пример 12. При каких значениях a уравнение 2x 4 – 2ax 2 + a 2 – 2 = 0 не имеет решений? Решение. Сделав замену y = x 2 , получим квадратное уравнение f(y) = 2y 2 – 2ay + a 2 – 2 = 0. Полученное уравнение не имеет решения, когда D Эти условия могут быть записаны в виде совокупности откуда Пример 13. При каждом значении параметра a решить уравнение cos x sin 2x = asin 3x. Решение. Так как 2cos x sin 2x = sin x + sin 3x и sin 3x = 3sin x – 4sin 3 x, то уравнение запишется в виде sin x (sin 2 x (4a – 2) – (3a – 2)) = 0. Отсюда получаем решения x = p n, n О Z при любом a. Уравнение имеет решения не совпадающие с решениями первого уравнения, только при условии Последние ограничения эквивалентны
Пример 14. Найти все значения параметра a, при каждом из которых неравенство Решение. Преобразуем неравенство к виду cos 2 x – 2acos x + a 2 + 2a – 3 > 0 и сделаем замену t = cos x. Важно заметить, что параметр t пробегает значения от – 1 до 1, поэтому задача переформулируется в таком виде: найти все a такие, что
выполняется при всех t О [– 1; 1]. Эту задачу мы уже решили ранее. Пример 15. Определить, при каких значениях a уравнение log3 (9 x + 9a 3 ) = x имеет решения, и найти их. Решение. Преобразуем уравнение к виду 9 x – 3 x + 9a 3 = 0 и, сделав замену y = 3 x , получим y 2 – y + 9a 3 = 0. В случае, когда дискриминант отрицательный, уравнение решений не имеет. Когда дискриминант D = 1 – 36a 3 = 0, уравнение имеет единственный корень Итак, окончательно получаем решений нет при остальных a. Пример 16. Для каждого значения параметра a решить уравнение sin 4 x + cos 4 x + sin 2 x + a = 0. Решение. Так как График функции, стоящей в левой части уравнения, – парабола с вершиной, абсцисса которой y0 = 1; значение функции в точке y = – 1 равно 1 – 2a; дискриминант уравнения равен 8a + 12. Это означает, что больший корень y2 уравнения y 2 – 2y – 2a – 2 = 0, даже если он существует, больше 1, и соответствующее уравнение sin 2x = y2 решений не имеет. Случай 1. если дискриминант отрицательный, т. е. a Случай 2. Если дискриминант равен Случай 3. Если дискриминант больше 0, т. е. Случай 4. Если f(– 1) = 0, т. е. Случай 5. Если дискриминант больше 0, т. е. Ответ: если если если если (Случаи описывает все возможные решения. – Прим. ред.) Задачи для самостоятельного решения 1. При каких значениях a уравнение ax 2 – 4x + 5 = 0 не имеет корней? Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение. 🎥 ВидеоРешение квадратных уравнений вида ax^2 + bx + c = 0. Формула корней квадратного уравненияСкачать  Тема: Квадратные уравнения. Урок: Уравнения вида y=ax^2 + bx +cСкачать  Математика| Разложение квадратного трехчлена на множители.Скачать  #118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать  Квадратное уравнение. 8 класс.Скачать  Решение биквадратных уравнений. 8 класс.Скачать  При каком значении параметра корни уравнения удовлетворяют условиюСкачать  Как решить НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ. Часть 1. Уравнение вида ax^2+c=0Скачать  Квадратное уравнение. Практическая часть. 2ч. 8 класс.Скачать  Дробно-рациональные уравнения. 8 класс.Скачать  ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать  |







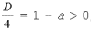
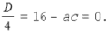
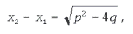
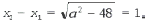
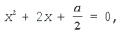
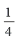 ,
, 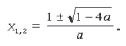
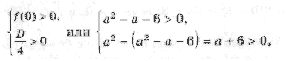
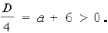
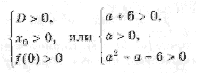
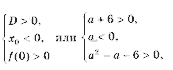
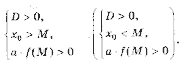
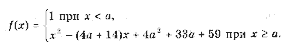
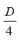 = – 5(a + 2) і 0,
= – 5(a + 2) і 0, 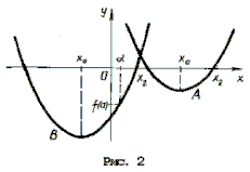
 .
. 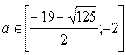 .
.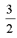 .
.
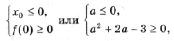
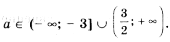
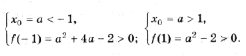
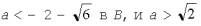
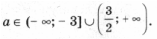
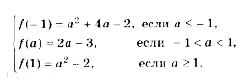
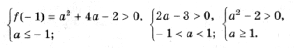
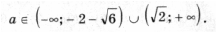
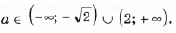
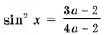
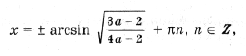
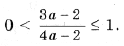
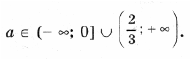
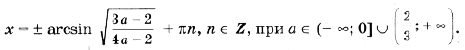
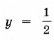 ,
, 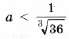 ,
, 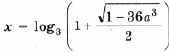 ,
, 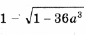 1 – положительно,
1 – положительно, 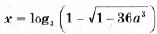 .
.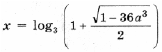
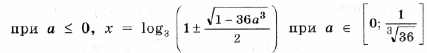
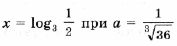 ,
,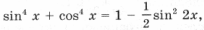
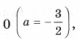
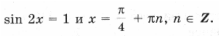
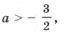
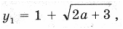
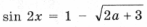 – имеет решения.
– имеет решения.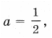 получаем уравнение
получаем уравнение 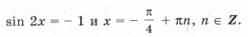
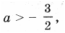 и, кроме того, f(– 1) 2 – 2y – 2a – 2 = 0 имеет корни
и, кроме того, f(– 1) 2 – 2y – 2a – 2 = 0 имеет корни 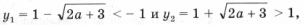
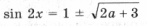 не имеют решений.
не имеют решений.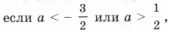 то решений нет;
то решений нет;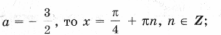
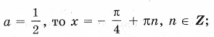
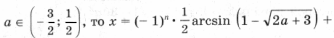
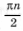
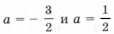 отдельно выделять не следует:
отдельно выделять не следует: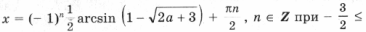
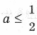
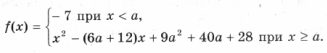
 .
.