Укажите ординату точки в которой график уравнения y 1 4 x 5 пересекает ось ординат

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Известно что график уравнения 4х — 5у = 1 проходит через точку, абциса которой равна 1?

Алгебра | 5 — 9 классы

Известно что график уравнения 4х — 5у = 1 проходит через точку, абциса которой равна 1.

Найдите ординату этой точки.

y = (4 — 1) / 5 = 3 / 5 ;

Видео:Найти ординату точки пересечения графиков двух линейных функцийСкачать

На графике функции y = 5x — 8 найдите точку, абсцисса который равна ее ординате?

На графике функции y = 5x — 8 найдите точку, абсцисса который равна ее ординате.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Дана функция y = x ^ 2 известно что произведение абсциссы и ординаты некоторой точки графика этой функций равно 125?

Дана функция y = x ^ 2 известно что произведение абсциссы и ординаты некоторой точки графика этой функций равно 125.

Найдите сумму абсциссы и ординаты этой точки.

Видео:Дан график производной Найти абсциссу точки в которой касательная к графику функции парал-на оси ХСкачать

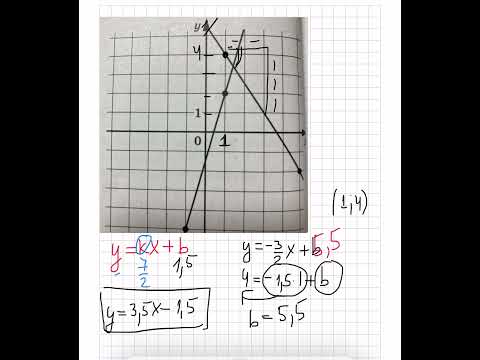
График уравнения 8х — 5х = 17 проходит через точку с абсциссой 2?

График уравнения 8х — 5х = 17 проходит через точку с абсциссой 2.

Найдите ординату этой точки.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Найди точку графика линейной функции y = 3x−3, абсцисса которой равна ординате?

Найди точку графика линейной функции y = 3x−3, абсцисса которой равна ординате.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Известно что график уравнения 3х — у = 4 проходит через точку М ордината которой равна 2 найдите абсциссу этой точки?

Известно что график уравнения 3х — у = 4 проходит через точку М ордината которой равна 2 найдите абсциссу этой точки.

Видео:Занятие 1. График линейной функции y=kx+bСкачать

Постройте прямую, являющуюся графиком уравнения — 2x + y = 3?

Постройте прямую, являющуюся графиком уравнения — 2x + y = 3.

Найдите по графику ординату точки, абцисса которой равна — 4.

Видео:Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

1. Принадлежит ли графику уравнения 2х – 5у = 1 точка :а) А (3 ; 1) ;б) В (–1 ; –1) ;в) С (–2 ; –1)?

1. Принадлежит ли графику уравнения 2х – 5у = 1 точка :

2. Постройте график линейного уравнения –4x + 3y = 6.

3. Известно, что график уравнения x + 2y = 2 проходит через точку А, абсцисса которой равна 2.

Найдите ординату этой точки.

Кто нибудь знает это хоть что нибудь решите плиз ).

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Помогите с задачей?

Помогите с задачей!

На прямой, являющейся графиком уравнения 21x — 5y = 100, взята точка, абсцисса которой равна 3.

Найдите ординату этой точки.

Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

На графике функций y = 3x + 8найдите точку, абсцисса которой равна ее ординате?

На графике функций y = 3x + 8

найдите точку, абсцисса которой равна ее ординате.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Найдите точку, в которой график уравнения 3x — y = 2 пересекает ось ординат?

Найдите точку, в которой график уравнения 3x — y = 2 пересекает ось ординат.

На этой странице сайта размещен вопрос Известно что график уравнения 4х — 5у = 1 проходит через точку, абциса которой равна 1? из категории Алгебра с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

3в 4 = 81 ; 2 в 3 = 8 ; 3 во 2 = 9 ; 4 в 3 = 64.

Видео:Как построить график линейной функции.Скачать

Парабола, график, вершина, нули.

теория по математике 📈 функции

Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax 2 +bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀= − b 2 a . . = 8 2 ∙ 2 . . = 8 4 . . = 2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х 2 +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

D=b 2 – 4ac=4 2 – 4 ∙ 1 ∙ ( − 5 ) = 36

Значит, нули функции равны –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀= − b 2 a . . = − 4 2 ∙ 2 . . = − 4 4 . . = − 1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

А) a>0, с >0 Б) а 0 В) а>0, с

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 – это график №1

Б) а 0 – это график №3

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3

pазбирался: Даниил Романович | обсудить разбор | оценить

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ОГЭ Задание 11 Графики функцииСкачать

Прямые на координатной плоскости

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Видео:№ 40130 РешуЕгэ найти абсциссу точки, в которой касательная к графику функции параллельна прямойСкачать

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

Видео:Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

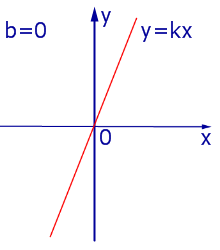Рис.1

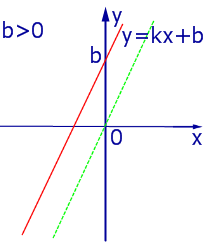Рис.2

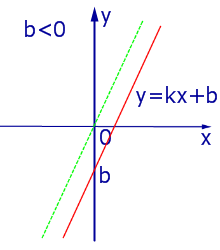Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

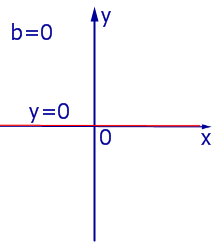Рис.4

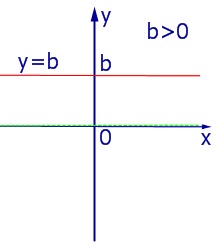Рис.5

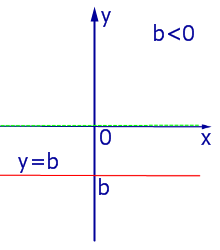Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны . имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов. y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии y = kx (2) равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2). Рис.10 Рис.11 Рис.12 Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле Видео:Задача 7 ЕГЭ по математике. Урок 15.Скачать 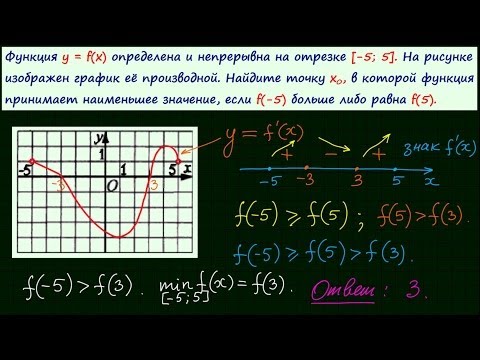Прямые, параллельные оси ординат Прямые, параллельные оси Oy , задаются формулой x = c , (3) где c – произвольное число, и изображены на рис. 13, 14, 15. Рис.13 Рис.14 Рис.15 Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:7 класс. Алгебра. Урок 5. ПРАКТИКА: Линейная функция (Часть 2)Скачать Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые px + qy = r , (4) где p, q, r – произвольные числа. В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию . что и требовалось. В случае, когда получаем: откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид 0 = r , (5) и при r = 0 его решением являются точки всей плоскости: В случае, когда уравнение (5) решений вообще не имеет. Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением px + qy = r1 , (6) параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением – qx + py = r2 , (7) перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и параллельной к прямой 4x + 5y = 7 ; (8) перпендикулярной к прямой (8). В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде 4x + 5y = r1 , (9) где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде – 5x + 4y = r2 , (10) где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать Как определить a, b и c по графику параболы Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это. Видео:Как построить график функции без таблицыСкачать 1 способ – ищем коэффициенты на графике Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2. Коэффициент (a) можно найти с помощью следующих фактов: — Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам. Ищем 3 точки с целыми координатами, принадлежащие параболе. Пример: Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями. Решаем систему. Пример: Вычтем из второго уравнения первое: Подставим (9a) вместо (b): Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье: Подставим в первое уравнение (a): Получается квадратичная функция: (y=-x^2-9x-15). Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи). Таким образом имеем систему: Сложим 2 уравнения: Подставим во второе уравнение: Теперь найдем точки пересечения двух функций: Теперь можно найти ординату второй точки пересечения: Видео:Как легко составить уравнение параболы из графикаСкачать 3 способ – используем преобразование графиков функций Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции. Главный недостаток этого способа — вершина должна иметь целые координаты. Сам способ базируется на следующих идеях: График (y=-x^2) симметричен относительно оси (x) графику (y=x^2). – Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз. – Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз. – График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц. — График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх. График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз. У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу: Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2). А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4). То есть наша функция выглядит так: (y=(x-5)^2-4). После раскрытия скобок и приведения подобных получаем искомую формулу: Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её: Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2). Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2). Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4). Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства