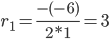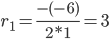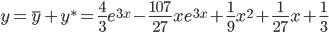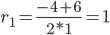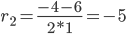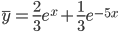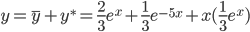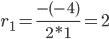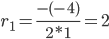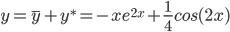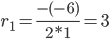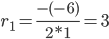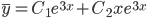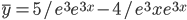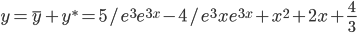Укажите частное решение дифференциального уравнения у 2у 4 удовлетворяющее начальному условию у 0 5

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Задача Коши онлайн

Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.

Найти решение задачи Коши для дифференциального уравнения:

при заданных начальных условиях:

При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:

удовлетворяющее начальным условиям:

Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:

Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:

Далее, поставляем начальные условия в функцию и её производную :

Решая полученную систему уравнений получаем значения произвольных постоянных и :

Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Другие полезные разделы:

Видео:Общее и частное решение дифференциального уравненияСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Пример решения дифференциального уравнения

Решение находим с помощью сервиса линейные дифференциальные уравнения с постоянными коэффициентами.
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x , y₂ = xe 3x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·x·e 3x
Найдем частное решение при условии:y(0) = 4/3, y'(0) = 1/27
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 4/3
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(0) = 3·c1+c2, то получаем второе уравнение:
3·c1+c2 = 1/27
В итоге получаем систему из двух уравнений:
c1 = 4/3
3·c1+c2 = 1/27
т.е.:
c₁ = 4 /₃, c₂ = -107 /₂₇
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = x 2 -x+3
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x 2 -x+3, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = x 2 -x+3
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = x 2 -x+3
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 1
-12A + 9B = -1
2A -6B + 9C = 3
Решая ее, находим:
A = 1 /₉;B = 1 /₂₇;C = 1 /₃;
Частное решение имеет вид:
y * = 1 /₉x 2 + 1 /₂₇x + 1 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №2. y″ +4y’ — 5y = 2·e x

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +4 r — 5 = 0
D = 4 2 — 4·1·(-5) = 36


Корни характеристического уравнения:
r₁ = 1
r₂ = -5
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x
y₂ = e -5x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·e -5x
Найдем частное решение при условии:y(0) = 1, y'(0) = -1
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную:
y’ = c1·e x -5·c2·e -5·x
Поскольку y'(0) = c1-5·c2, то получаем второе уравнение:
c1-5·c2 = -1
В итоге получаем систему из двух уравнений:
c1+c2 = 1
c1-5·c2 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 2 /₃, c₂ = 1 /₃
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 2·e x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = 0, α = 1, β = 0.
Следовательно, число α + βi = 1 + 0i является корнем характеристического уравнения кратности k = 1(r₁).
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные: y’ = A·e x (x+1)
y″ = A·e x (x+2)
которые подставляем в исходное дифференциальное уравнение:
y″ + 4y’ -5y = (A·e x (x+2)) + 4(A·e x (x+1)) -5(x (Ae x )) = 2·e x
или
6·A·e x = 2·e x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
6A = 2
Решая ее, находим:
A = 1 /₃;
Частное решение имеет вид:
y * = x ( 1 /₃e x )
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №3. y″ — 4y’ + 4y = 2sin(2x), y(0) = 0. y'(0) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -4 r + 4 = 0
D = (-4) 2 — 4·1·4 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 2x
y₂ = xe 2x
Общее решение однородного уравнения имеет вид: y = C₁·e 2x +C₂·x·e 2x
Найдем частное решение при условии:y(0) = 0, y'(0) = -1
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 0
Находим первую производную:
y’ = 2·c1·e 2·x +2·c2·x·e 2·x +c2·e 2·x
Поскольку y'(0) = 2·c1+c2, то получаем второе уравнение:
2·c1+c2 = -1
В итоге получаем систему из двух уравнений:
c1 = 0
2·c1+c2 = -1
т.е.:
c₁ = 0, c₂ = -1
Тогда частное решение при заданных начальных условиях можно записать в виде:
y =-x·e 2x
Рассмотрим правую часть: f(x) = 2·sin(2·x)
Поиск частного решения.
Здесь P(x) = 0, Q(x) = 2, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2·B·cos(2x)-2·A·sin(2x)
y″ = -4(A·cos(2x)+B·sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y″ -4y’ + 4y = (-4(A·cos(2x)+B·sin(2x))) -4(2·B·cos(2x)-2·A·sin(2x)) + 4(Acos(2x) + Bsin(2x)) = 2·sin(2·x)
или
8·A·sin(2x)-8·B·cos(2x) = 2·sin(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A = 2
0A -8B = 0
Решая ее, находим:
A = 1 /₄;B = 0;
Частное решение имеет вид:
y * = 1 /₄cos(2x) + 0sin(2x)
или
y * = 1 /₄cos(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №4. Найти частное решение, общее решение и решение задачи Коши уравнения: y″ — 6y’ + 9y = 9x 2 +6x + 2, y(1) = 1, y'(1) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x
y₂ = xe 3x
Общее решение однородного уравнения имеет вид:

Найдем частное решение при условии:y(1) = 1, y'(1) = -1
Поскольку y(1) = c1·e 3 +c2·e 3 , то получаем первое уравнение:
c1·e 3 +c2·e 3 = 1
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(1) = 3·c1·e 3 +4·c2·e 3 , то получаем второе уравнение:
3·c1·e 3 +4·c2·e 3 = -1
В итоге получаем систему из двух уравнений:
c1·e 3 +c2·e 3 = 1
3·c1·e 3 +4·c2·e 3 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 5/e 3 , c₂ = -4/e 3
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 9·x 2 +6·x+2
Поиск частного решения.
Здесь P(x) = 9·x 2 +6·x+2, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = 9·x 2 +6·x+2
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = 9·x 2 +6·x+2
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 9
-12A + 9B = 6
2A -6B + 9C = 2
Решая ее, находим:
A = 1;B = 2;C = 4 /₃;
Частное решение имеет вид:
y * = x 2 + 2x + 4 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Видео:Частное решение ДУ, с помощью рядаСкачать

Найти частное решение дифференциального уравнения у» + 2у + 4 = 0 ; у(0) = 5?

Математика | 10 — 11 классы

Найти частное решение дифференциального уравнения у» + 2у + 4 = 0 ; у(0) = 5.

Недостаточно условий, для нахождения частного решения ДУ второго порядка необходимы условия y(0) = .

У вас только у(0) = 5.

Без второго условия не найти второй коэффициент.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Найти общее решение дифференциальных уравнений первого порядка?

Найти общее решение дифференциальных уравнений первого порядка.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Найти частное решение дифференциального уравнения : (ху ^ 2 + x)dx + (x ^ 2y — y)dy = 0 y(0) = 1?

Найти частное решение дифференциального уравнения : (ху ^ 2 + x)dx + (x ^ 2y — y)dy = 0 y(0) = 1.

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Найти общее решение дифференциального уравнения?

Найти общее решение дифференциального уравнения.

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Найти общее решение дифференциального уравнения и частное решение удовлетворяющее начальному условию?

Найти общее решение дифференциального уравнения и частное решение удовлетворяющее начальному условию.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

(а) Найти общее решение дифференциальных уравнений второго порядка?

(а) Найти общее решение дифференциальных уравнений второго порядка.

(а) (б) Указать вид частного решения для данного неоднородного уравнения, найти общее решение соответствующего однородного уравнения и найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

(б) y» — y’ + y = x ^ 3 + 6.

Видео:Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее начальным условиям интересует очень подробное решение?

Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее начальным условиям интересует очень подробное решение.

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Дифференциальное уравнение найти частное решение удовлетворяющее заданному начальному уравнению dy / dx = 5e ^ 2x / y ^ 2?

Дифференциальное уравнение найти частное решение удовлетворяющее заданному начальному уравнению dy / dx = 5e ^ 2x / y ^ 2.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Найти общее решение дифференциального уравнения y» + 2y’ = 0?

Найти общее решение дифференциального уравнения y» + 2y’ = 0.

Видео:Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Найти общее решение дифференциального уравнения и частное решение удовлетворяющее начальному условию y = y0 при x = x0 y’ + y = e ^ ( — x) / (1 + x ^ 2) решение?

Найти общее решение дифференциального уравнения и частное решение удовлетворяющее начальному условию y = y0 при x = x0 y’ + y = e ^ ( — x) / (1 + x ^ 2) решение.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Найти общее решение дифференциального уравнения?

Найти общее решение дифференциального уравнения.

На этой странице находится вопрос Найти частное решение дифференциального уравнения у» + 2у + 4 = 0 ; у(0) = 5?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

5 + х = 5 х = 5 — 5 х = 0. У + 15 = 15 у = 15 — 15 у = 0. Х — 4 = 0 х = — 4. 28 — а = 28 а = 28 + 28 а = 56.

А) x = 5 — 5 = 0 b)y = 15 — 15 = 0 c)x = 0 + 4 = 4 d)a = 28 — 28 = 0.

А) 280, 70, 350, 20 б) 4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г) 5000000, 32000000.

А)280, 70, 350, 20 б)4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г)5000000, 32000000.

Представим, что x — это сколько страниц занимает расскуз, тогда x×3 — это сколько страниц занимает повесть x + (x×3) = 68 x + 3x = 68 4x = 68 x = 68 : 4 x = 17 — рассказ 17×3 = 51 — повесть.

Т. к. Собрали всего 61 орех, а вова собрал четное число, то остальные дети в сумме собрали нечетное количество( т. К. 61 — четное число = нечетное) и т. К. они собирали только нечетное количество значит детей было нечетное число( т. К. нечетное п..

1) 33 : 3 = 11 (кусков) картона разрезали 2) 17 — 11 = 6 (кусков) картона Ответ : 6 кусков картона осталось неразрезанными.

1)1000 : 100 = 10 2)904 3)450 : 10 = 45 4)1000 : 10 = 100 5)200 — 100 = 100.

1) 7(х + у) / 21 = х + у / 3 2)4(2m — n) / 4m = 2m — n / m 3)3(3a + 4b) / 3 = 3a + 4b 4)9(5c + 2d) / 27d = 5c + 2d / 3d 5)x(5 — y) / x = 5 — y 6)2m(3n — 2) / 2m = 3n — 2.

Возможно одинакого. Если Аня поймала 4, а Вера — 1 Боря — 3, Гена — 2.

📽️ Видео

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать