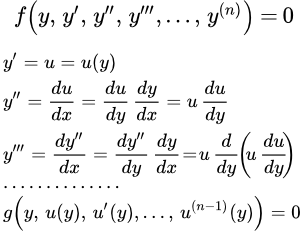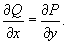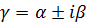Указать уравнения не содержащие явно переменную x (8 видео)

Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Содержание

Метод решения
Пример
Дифференциальные уравнения, допускающие понижение порядка
Понижение порядка уравнения, не содержащего y и y‘
Понижение порядка уравнения, не содержащего y
Понижение порядка уравнения, не содержащего x
Уравнения, не содержащие явно независимой переменной
📺 Видео

Видео:ДУ высших порядков, не содержащие независимую переменную.Скачать

Метод решения

Рассмотрим уравнение, не содержащее независимую переменную в явном виде:
(1) .
Порядок этого уравнения понижается на единицу с помощью подстановки:

Далее считаем, что функция u зависит от переменной y , тогда:
;
;
и т. д.

В результате такой подстановки, порядок уравнения понижается на единицу.

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 1). Высшая математика.Скачать

Пример

Уравнение не содержит независимую переменную в явном виде. Делаем подстановку:
.
Считаем, что функция u зависит от переменной y . Тогда
.

Подставляем в исходное уравнение:
.
Делим на u . При имеем:
.
Это уравнение с разделяющимися переменными. Делим на и умножаем на dy . При имеем:
.
Интегрируем:
(2) .

Подставляем в (2):
.
Потенцируем:
.
Заменим постоянную интегрирования . Знак модуля сводится к умножению на &pm;1 . Включим &pm;1 в постоянную . То есть мы теперь полагаем, что может быть не только положительным, но и отрицательным числом. Тогда:
.

Выполняем преобразования:
;
.
При имеем:
;
.

Разделяем переменные:
.
Интегрируем:
(3) .

Вычисляем интеграл:

.
Подставляем в (3):
;
.
Возводим в квадрат и выполняем преобразования:
;
;
(4) .

При выводе формулы (4) мы предполагали, что
и .
Теперь рассмотрим случаи
.
Нетрудно видеть, что решение, охватывающее эти три равенства, есть
(5) ,
где C – произвольная постоянная. Тогда . Подставляя это в исходное уравнение нетрудно убедиться, что оно выполняется. Это особое решение. Добавим его в ответ.

Автор: Олег Одинцов . Опубликовано: 18-07-2013 Изменено: 27-06-2018

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим три частных случая решения дифференциальных уравнений с возможностью понижения порядка. Во всех случаях понижение порядка производится с помощью замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Понижение порядка уравнения, не содержащего y и y‘

Это дифференциальное уравнение вида . Произведём замену переменной: введём новую функцию и тогда . Следовательно, и исходное уравнение превращается в уравнениие первого порядка

с искомой функцией .

Решая его, находим . Так как , то .

Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

где и — произвольные константы интегрирования.

Пример 1. Найти общее решение дифференциального уравнения

Решение. Произведём замену переменной, как было описано выше: введём функцию и, таким образом, понизив порядок уравнения, получим уравнение первого порядка . Интегрируя его, находим . Заменяя на и интегрируя ещё раз, находим общее решение исходного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение третьего порядка

Решение. Дифференциальное уравнение не содержит y и y‘ в явном виде. Для понижения порядка применяем подстановку:

Тогда и получаем линейное дифференциальное уравнение первого порядка:

Заменяя z произведением функций u и v , получим

Тогда получим выражения с функцией v :

Выражения с функцией u :

Дважды интегрируем и получаем:

Интегрируем по частям и получаем:

Итак, общее решение данного дифференциального уравения:

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 3). Высшая математика.Скачать

Понижение порядка уравнения, не содержащего y

Это дифференциальное уравнение вида . Произведём замену переменной как в предыдущем случае: введём , тогда , и уравнение преобразуется в уравнение первого порядка . Решая его, найдём . Так как , то . Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

где и — произвольные константы интегрирования.

Пример 3. Найти общее решение дифференциального уравнения

Решение. Уже знакомым способом произведём замену переменной: введём функцию и понизим порядок уравнения. Получаем уравнение первого порядка . Решая его, находим . Тогда и получаем решение исходного дифференциального уравнения второго порядка:

Пример 4. Решить дифференциальное уравнение

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

Получим дифференциальное уравнение первого порядка:

Это уравение с разделяющимися переменными. Решим его:

Интегрируем полученную функцию:

Мы пришли к цели — общему решению данного дифференциального уравения:

Пример 5. Найти общее решение дифференциального уравнения

Получим дифференциальное уравнение первого порядка:

Это однородное уравение, которое решается при помощи подстановки . Тогда , :

Далее потребуется интегрировать по частям. Введём обозначения:

Таким образом, получили общее решение данного дифференциального уравения:

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Понижение порядка уравнения, не содержащего x

Это уравнение вида . Вводим новую функцию , полагая . Тогда

Подставляя в уравнение выражения для и , понижаем порядок уравнения. Получаем уравнение первого порядка относительно z как функции от y:

Решая его, найдём . Так как , то . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:

где и — произвольные константы интегрирования.

Пример 6. Найти общее решение дифференциального уравнения

Решение. Полагая и учитывая, что , получаем . Понизив порядок исходного уравнения, получаем уравнение первого порядка с разделяющимися переменными. Приводя его к виду и интегрируя, получаем , откуда . Учитывая, что , находим , откуда получаем решение исходного дифференциального уравнения второго порядка:

При сокращении на z было потеряно решение уравнения , т.е. . В данном случае оно содержится в общем решении, так как получается из него при (за исключением решения y = 0).

Пример 7. Найти общее решение дифференциального уравнения

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

Получим дифференциальное уравнение первого порядка:

Это уравение с разделяющимися переменными. Решим его:

Используя вновь подстановку

получим ещё одно уравнение с разделяющимися переменными. Решим и его:

Таким образом, общее решение данного дифференциального уравения:

Пример 8. Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0) = 1 , y‘(0) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Поэтому применяем подстановку:

Таким образом, понизили порядок уравнения и получили уравнение первого порядка

Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:

Чтобы определить C 1 , используем данные условия y(0) = 1 , y‘(0) = −1 или p(0) = −1 . В полученное выражение подставим y = 1 , p = −1 :

Разделяя переменные и интегрируя, получаем

Из начального условия y(0) = 1 следует

Получаем окончательное решение данного дифференциального уравнения

Пример 9. Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1) = 1 , y‘(1) = −1 .

Таким образом, получили уравнение первого порядка

Это дифференциальное уравнение с разделяющимися переменными. Разделив обе части уравнения на p , получим

Интегрируем обе части уравнения

Используем начальные условия и определим C 1 . Если x = 1 , то y = 1 и p = y‘ = −1 , поэтому

Из начального условия y(1) = 1 следует

Получаем окончательное решение данного дифференциального уравнения

Видео:Диффуры, не содержащие искомую функцию yСкачать

Уравнения, не содержащие явно независимой переменной

Определение уравнения в полных дифференциалах

Дифференциальное уравнение вида

называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение

Общее решение уравнения в полных дифференциалах определяется формулой

где C − произвольная постоянная.

Необходимое и достаточное условие

Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:

42) Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.

Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида
F(x, y,y‘, y», . y (n) ) = 0,
где F — известная функция (n+2) переменных, определенная в области DÌR n +2, x — независимая переменная из интервала (a, b), y =y(x) — неизвестная функция, n — порядок уравнения.

, (1)

где x — независимая переменная, y — искомая функция, а функция F определена и непрерывна в некоторой области и во всяком случае зависит от , называется обыкновенным дифференциальным уравнением n -го порядка.

Рассмотрим некоторые типы уравнений высших порядков, допускающие понижение порядка.

Уравнения, не содержащие искомой функции и нескольких последовательных производных.

Рассмотрим уравнения вида

. (2)

С помощью замены , где u — новая неизвестная функция, уравнение (2) приводится к уравнению (n-k) -го порядка:

Уравнения, не содержащие явно независимой переменной.

Рассмотрим уравнения вида

. (3)

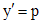
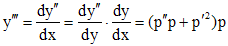
С помощью замены (где p=p(y) — новая искомая функция независимая переменная) порядок уравнения (3) понижается на единицу, так как

Данная подстановка дает уравнение (n-1) — го порядка относительно новой неизвестной функции p:

При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения (3) решений такого вида.

43) Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

Линейным однородным уравнением -го порядка с постоянными коэффициентами называется уравнение вида

(1)

где коэффициенты – некоторые действительные числа. Для нахождения частных решении уравнения (1) составляют характеристическое уравнение

(2)

которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n степени и имеет n корней.

Тогда общее решение дифференциального уравнения (1) строится в зависимости от характера корней уравнения (2):

1.каждому действительному простому корню k в общем решении соответствует слагаемое вида ;

2.каждому действительному корню кратности 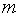в общем решении соответствует слагаемое вида ;

3.каждой паре комплексных сопряженных простых корней и в общем решении соответствует слагаемое вида

4.каждой паре комплексных сопряженных корней и кратности в общем решении соответствует слагаемое вида

51) Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора.

Ряд Тейлора

Основные разложения в ряд Тейлора

53)Ряд Лорана — двусторонне бесконечный степенной ряд по целым степеням 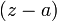, то есть ряд вида

Этот ряд понимается как сумма двух рядов:

1. — положительная часть ряда Лорана (иногда называется правильной) и

2. — отрицательная часть ряда Лорана (иногда называется главной).

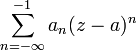
При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Область сходимости ряда по положительным степеням разложения функции в ряд есть сфера радиуса сходимости

. В области этой сферы лежит и область сходимости ряда по изолированному направлению делителей нуля. Если R=0, то ряд сходится только в точке a, если , то ряд сходится во всем пространстве Y.

Ряд по отрицательным степеням разложения функции сходится в сфере сходимости >r. Если r

50) Функциональные ряды в комплексной области

Понятия последовательности функций комплексной переменной (сокр. ФКП), ФР ФКП и его поточечной сходимости вводятся аналогично этим понятиям в действительной области. Область определения, область сходимости строятся на –плоскости.

Степенным рядом с комплексными членами называется ряд вида

где a0, a1, a2, …, an, — постоянные комплексные числа (коэффициенты ряда), z0 — фиксированное комплексное число (центр круга сходимости).

Теорема Абеля. Если степенной ряд сходится в точке z1 ≠ z0, то он абсолютно сходится в любой точке круга | z — z0| | z2 — z0| (т.е. находящейся дальше от точки z0, чем z2).

Из теоремы Абеля следует существование такого неотрицательного действительного числа R, что ряд абсолютно сходится в любой внутренней точке круга радиуса R с центром в точке z0, и расходится в любой точке вне этого круга. Число R называется радиусом сходимости, круг — кругом сходимости. В точках границы этого круга — окружности | z — z0| = R радиуса R с центром в точке z0 — ряд может и сходиться, и расходиться.

44) Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

Называется уравнение вида:

(1)

Где а1, а2, …, аn постоянные действительные числа.

Решение этого уравнения можно записать в виде:

Y= ,

А частное решение можно найти с помощью метода вариаций.

Если правая часть имеет специальный вид, то частное решение можно найти методом “подбора”. Общий вид правой части уравнения (1) при котором можно применять метод подбора следующий:

F(x)= ,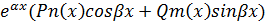

Где Pn и Qm многочлены.

Рассмотрим некоторые частные случаи:

1)F(x)=Pn(x), =0 если число совпадает с корнями характеристического ур-ния и S- число совпадений, то говорят что есть резонанс в степени S.

Если нет резонанса, то частное решение ищем в виде:

, где — многочлен n-ой степени с неопределёнными коэффициентами.

представляя данное решение в исходное уравнение.

, то частное решение ищем в виде :

f(x)=Pn(x) ,

если нет резонанса:

f(x) = Pn(x)cos +Qn(x)sin ,

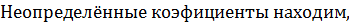
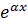
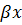
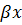
Если нет резонанса, то:

cos + , k=max[n,m];

( cos + ;

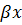
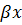
Если правая часть представляет собой сумму выражений специального вида, то находим несколько частных решений и их складываем.

46) Функции комплексной переменной. Предел и непрерывность функции комплексной переменной.

Если каждой точке z = х + iy некоторого множества Е поставленно в соответствие одно или несколько комплексных чисел w = и + iv, то говорят, что на множестве Е определена функция (однозначная или многозначная) комплексного переменного w = f(z).

Функцию f(z) можно рассматривать как пару функций и<х,у) и v<x,y).

Предел и непрерывность функции комплексной переменной:

Число А называется ó(