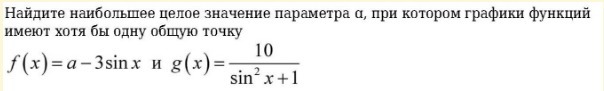Указать наибольшее целое значение параметра а при котором уравнение имеет

Математика | 10 — 11 классы

Найдите наибольшее целое значение параметр а.

Попробую решить алгебраически.

Если графики имеют общую точку, то в этой точке f(x0) = g(x0)

a — 3sin x = 10 / (sin ^ 2 x + 1)

Так как sin x ∈ [ — 1 ; 1], то sin ^ 2 x ∈ [0 ; 1] ; sin ^ 2 x + 1 ∈ [1 ; 2]

То есть sin ^ 2 x + 1 > = 1 при любом x, поэтому 10 / (sin ^ 2 x + 1).

A = 3sin(x) + 10 / (sin ^ 2(x) + 1) строим график правой части и находим нужную горизонтальную линию а.

Видео:Найдите все значения параметра m≦100 , при которых уравнение σ(x)=m имеет решениеСкачать

Найти количество всех целых значений параметра а, при которых уравнение имеет корни?

Найти количество всех целых значений параметра а, при которых уравнение имеет корни.

Видео:Наибольшее и наименьшее значение функции. 10 класс.Скачать

Найти все целые значения параметра b, при которых уравнение bx = 22 имеет целый корень?

Найти все целые значения параметра b, при которых уравнение bx = 22 имеет целый корень.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Найдите количество целых значений параметра a , при каждом из которых неравенство x−ax−6a?

Найдите количество целых значений параметра a , при каждом из которых неравенство x−ax−6a.

Видео:Уравнение с параметром | Математика TutorOnlineСкачать

Найдите наибольшее целое значение х , при котором верно неравенство х ≤ — 12?

Найдите наибольшее целое значение х , при котором верно неравенство х ≤ — 12.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Найдите наибольшее целое значение , при котором верно неравенство x 5 мар. 2021 г., 10:31:06 | 5 — 9 классы

Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Найдите наибольшее целое значение x, при котором верно неравенство больше — 14?

Найдите наибольшее целое значение x, при котором верно неравенство больше — 14.

Видео:Задача 18 ЕГЭ по математике #3Скачать

При каком наибольшем целом значении параметра a из отрезков с длинами 1, a — 3, a / 2 + 5 можно составить треугольник?

При каком наибольшем целом значении параметра a из отрезков с длинами 1, a — 3, a / 2 + 5 можно составить треугольник?

Видео:Найдите все значения а, при каждом из которых уравнение 64x^6+4x^2=(3x+a)^3+3x+a не имеет корней.Скачать

Найдите наибольшее целое значение X при котором верно неравенство X?

Найдите наибольшее целое значение X при котором верно неравенство X.

Видео:Математика ОГЭ Неравенство с параметромСкачать

Найдите наибольшее целое значение х(икс), при котором верно нервенство х?

Найдите наибольшее целое значение х(икс), при котором верно нервенство х.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Найдите наибольшее целое значение функции y = 2, 4 sinx?

Найдите наибольшее целое значение функции y = 2, 4 sinx.

На этой странице находится вопрос Найдите наибольшее целое значение параметр а?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Урок по теме «Методы решения задач с параметрами»

Разделы: Математика

Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.

Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Пример 1. Найдите все значения параметра a, при которых уравнение:

(2a – 1)x 2 + ax + (2a – 3) =0 имеет не более одного корня.

При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2 , то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:

Чтобы записать окончательный ответ, необходимо понять,

2. Графический метод.

В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).

Пример 2. Для каждого значения параметра a определите количество решений уравнения .

Заметим, что количество решений уравнения равно количеству точек пересечения графиков функций и y = a.

График функции показан на рис.1.

y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a 25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых уравнение = —ax +3a +2 имеет единственное решение.

Будем решать это уравнение заменой переменных. Пусть = t , t ≥ 0 , тогда x = t 2 + 8 и уравнение примет вид at 2 + t + 5a – 2 = 0 . Теперь задача состоит в том, чтобы найти все а, при которых уравнение at 2 + t + 5a – 2 = 0 имеет единственное неотрицательное решение. Это имеет место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t = 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.

Задача № 1. При каких значениях параметра b уравнение не имеет корней?

Ⅱ . Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a, при которых множество решений неравенства:

содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

.

Преобразуем обе части неравенства.

Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:

Рис.4

При a > 6 множество решений неравенства: .

Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).

Это

Ⅲ . Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.

1) Графиком дробно-линейной функции является гипербола. По условию x > 0. При неограниченном возрастании х дробь монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.

2) По определению степени область определения D(y) состоит из решений неравенства . При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.

3) При 0 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства . Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием а возрастает и неравенство равносильно неравенству . Если a ≥ 5 , то любое положительное число является его решением, и указанную в условии сумму нельзя найти. Если 1 . Так как возрастает на , то z(3) .

Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Задачи с параметром

1. Задача.
При каких значениях параметра a уравнение ( a — 1) x 2 + 2 x + a — 1 = 0 имеет ровно один корень?

1. Решение.
При a = 1 уравнение имеет вид 2 x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем уравнение относительно параметра a 4 a 2 — 8 a = 0, откуда a = 0 или a = 2.

1. Ответ: уравнение имеет единственный корень при a О .

2. Задача.
Найти все значения параметра a , при которых имеет два различных корня уравнение x 2 +4 ax +8 a +3 = 0.
2. Решение.
Уравнение x 2 +4 ax +8 a +3 = 0 имеет два различных корня тогда и только тогда, когда D = 16 a 2 -4(8 a +3) > 0. Получаем (после сокращения на общий множитель 4) 4 a 2 -8 a -3 > 0, откуда

2. Ответ:

3. Задача.
Известно, что
f 2 ( x ) = 6 x — x 2 -6.
а) Постройте график функции f 1 ( x ) при a = 1.
б) При каком значении a графики функций f 1 ( x ) и f 2 ( x ) имеют единственную общую точку?

3. Решение.
3.а. Преобразуем f 1 ( x ) следующим образом
График этой функции при a = 1 изображен на рисунке справа.
3.б. Сразу отметим, что графики функций y = kx + b и y = ax 2 + bx + c ( a № 0) пересекаются в единственной точке тогда и только тогда, когда квадратное уравнение kx + b = ax 2 + bx + c имеет единственный корень. Используя представление f 1 из 3.а , приравняем дискриминант уравнения a = 6 x — x 2 -6 к нулю. Из уравнения 36-24-4 a = 0 получаем a = 3. Проделав то же самое с уравнением 2 x — a = 6 x — x 2 -6 найдем a = 2. Нетрудно убедиться, что эти значения параметра удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.

4. Задача.
Найти все значения a , при которых множество решений неравенства x 2 -2 ax -3 a і 0 содержит отрезок [3;6].

4. Решение.
Первая координата вершины параболы f ( x ) = x 2 -2 ax -3 a равна x 0 = a . Из свойств квадратичной функции условие f ( x ) і 0 на отрезке [3;6] равносильно совокупности трех систем

Решением первой системы является множество (- Ґ ,1]. Вторая и третья система решений не имеют.

4. Ответ: a О (- Ґ ,1].

5. Задача (9 кл.)
При каком наименьшем натуральном значении a уравнение

x 2 +2 ax -3 a +7 = 2 x

имеет ровно два решения?

5. Решение.
Перепишем это уравнение в виде x 2 + (2 a -2) x — 3 a +7 = 0. Это квадратное уравнение, оно имеет ровно два решения, если его дискриминант строго больше нуля. Вычисляя дискриминант, получаем, что условием наличия ровно двух корней является выполнение неравенства a 2 + a -6 > 0. Решая неравенство, находим a a > 2. Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим натуральным решением второго является число 3.

6. Задача (10 кл.)
Найти все значения a , при которых график функции

f ( x ) =

x 2 + | ax +2 | a -1

проходит через точку с координатами (-1;1).

6. Решение.
Из условия f (-1) = 1 имеем уравнение

1 =

1+ | — a +2 | a -1

,

или, после очевидных преобразований, a -2 = | 2- a | . Последнее уравнение равносильно неравенству a і 2.

6. Ответ: a О [2; Ґ ).

7. Задача (10 кл.)
При каких значениях a сумма квадратов корней уравнения

x 2 -2 ax + a 2 — a = 0

больше чем 12?

7. Решение.
Дискриминант уравнения x 2 -2 ax + a 2 — a = 0 равен 4 a . Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x 1 + x 2 = 2 a и x 1 · x 2 = a 2 — a . Отсюда x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 -2 x 1 · x 2 = 2 a 2 +2 a . Решениями неравенства 2 a 2 +2 a > 12, удовлетворяющими условию a і 0, являются числа a > 2.

💥 Видео

Как решать неравенства? Часть 1| МатематикаСкачать

Уравнение в целых числах с параметромСкачать

При каких значениях параметра уравнение имеет единственный кореньСкачать

Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

Найдите все значения параметра a, при каждом из которых уравнение имеет ровно два различных корняСкачать

Найдите наименьшее и наибольшее значение выраженияСкачать

Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезкеСкачать

Уравнения с параметром. Алгебра 7 класс.Скачать