- Определение угла между прямыми
- Угол между прямыми на плоскости
- Угол между прямыми заданными уравнениями с угловым коэффициентом
- Угол между прямыми через направляющие векторы этих прямых
- Угол между прямыми через векторы нормалей этих прямых
- Угол между прямыми через направляющий вектор и вектор нормали этих прямых
- Примеры задач на вычисления угла между прямыми на плоскости
- Угол между прямыми в пространстве
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- Угол между прямой и плоскостью: определение, примеры нахождения
- Угол между прямой и плоскостью – определение
- Нахождение угла между прямой и плоскостью
- 💥 Видео
Видео:Угол между прямыми на плоскостиСкачать

Определение угла между прямыми
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между прямыми на плоскости
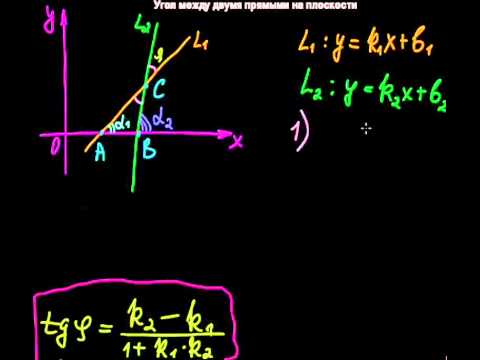
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Видео:14. Угол между прямыми в пространствеСкачать

Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор , для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Видео:§16 Угол между двумя прямыми на плоскостиСкачать
Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то — направляющий вектор первой прямой, направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор .
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
— направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Видео:Видеоурок "Угол между прямыми"Скачать

Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
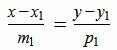 , , | (1.1) |
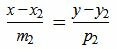 , , | (1.2) |
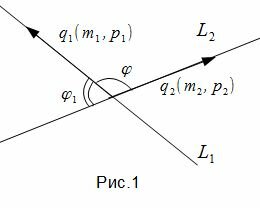
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
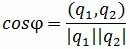 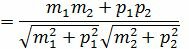 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
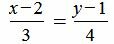 . . | (1.5) |
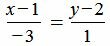 . . | (1.6) |
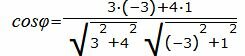 . . |
Упростим и решим:
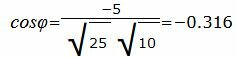 . . |
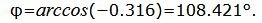 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
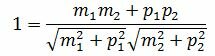 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
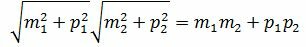 , , |
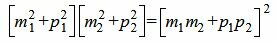 , , |
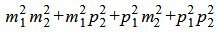 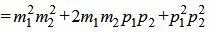 , , |
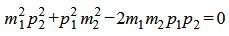 , , |
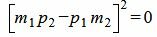 , , |
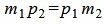 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
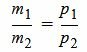 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
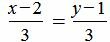 . . | (1.10) |
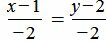 . . | (1.11) |
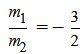 , , 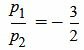 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
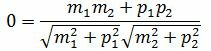 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
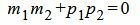 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
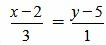 | (1.14) |
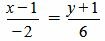 . . | (1.15) |
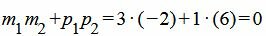 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
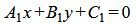 | (1.17) |
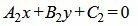 . . | (1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
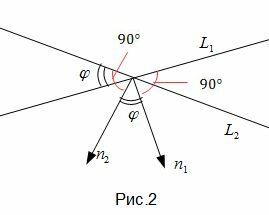 . . |
Из определения скалярного произведения двух векторов, имеем:
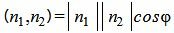 . . | (1.19) |
Из уравнения (19) получим
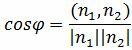 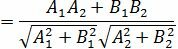 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
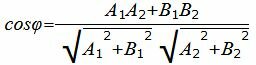 | (23) |
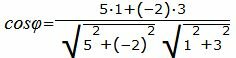 |
Упростим и решим:
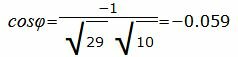 |
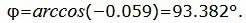 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
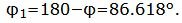 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
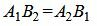 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
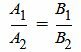 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:10 класс, 9 урок, Угол между прямымиСкачать

2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
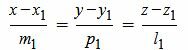 , , | (2.1) |
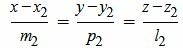 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
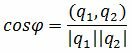 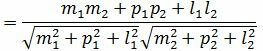 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
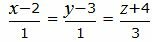 . . | (2.5) |
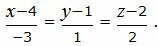 | (2.6) |
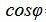 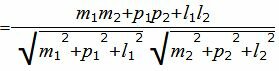 . . |
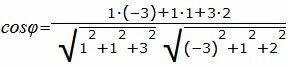 . . |
Упростим и решим:
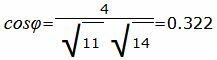 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
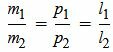 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
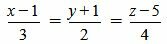 . . | (2.9) |
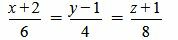 . . | (2.10) |
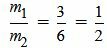 , , 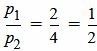 , , 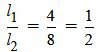 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
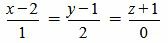 . . | (2.11) |
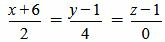 . . | (2.12) |
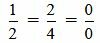 . . | (2.13) |
Выражение (2.13) нужно понимать так:
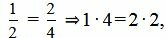 , , 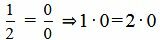 , , 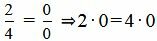 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
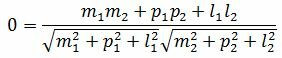 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
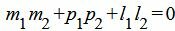 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
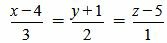 | (2.17) |
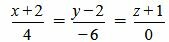 . . | (2.18) |
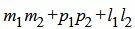 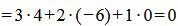 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Видео:Угол между прямыми в пространстве. 11 класс.Скачать
Угол между прямой и плоскостью: определение, примеры нахождения
Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Видео:9. Угол между прямымиСкачать

Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
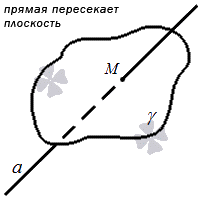
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
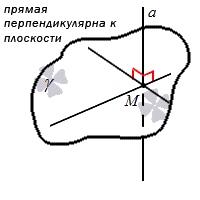
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
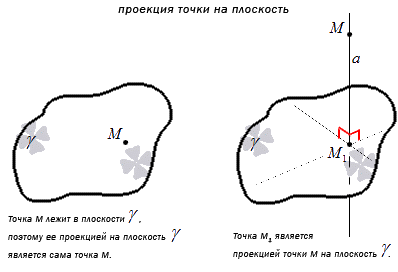
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ , проходящей через точку M , при условии, что она не принадлежит плоскости γ .
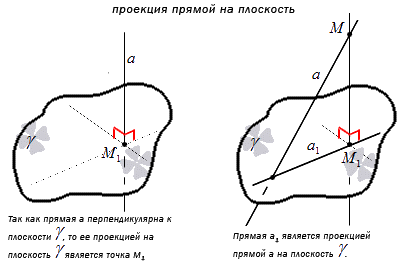
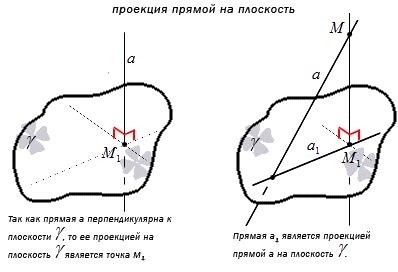
Проекция прямой а на плоскость γ — это множество проекций всех точек заданной прямой на плоскость.
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
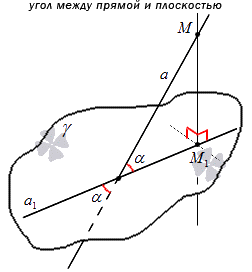
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Видео:Видеоурок "Угол между прямыми в пространстве"Скачать
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
Если в трехмерном пространстве вводится прямоугольная система координат О х у z , тогда в ней задается прямая a , пересекающая плоскость γ в точке M , причем она не перпендикулярна плоскости. Необходимо найти угол α , находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат О х у z задается прямая a , которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости γ соответствует уравнение плоскости и нормальный вектор плоскости. Тогда a → = ( a x , a y , a z ) является направляющим вектором заданной прямой a , а n → ( n x , n y , n z ) — нормальным вектором для плоскости γ . Если представить, что у нас имеются координаты направляющего вектора прямой a и нормального вектора плоскости γ , тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов a → и n → , исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
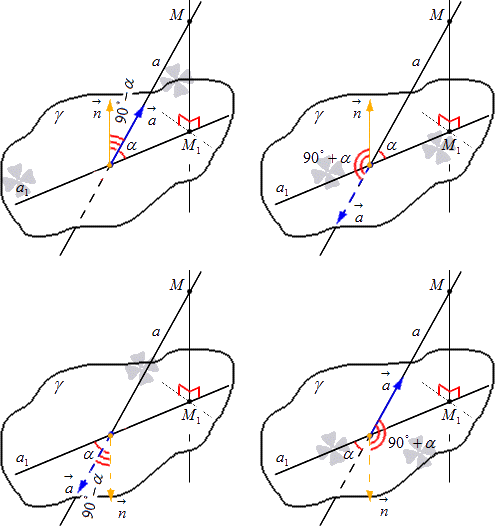
Необходимо отложить векторы a → и n → , начиная от точки пересечения прямой a с плоскостью γ . Существуют 4 варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все 4 вариации.
Отсюда получаем, что угол между векторами a → и n → имеет обозначение a → , n → ^ и является острым, тогда искомый угол α , располагающийся между прямой и плоскостью, дополняется, то есть получаем выражение вида a → , n → ^ = 90 ° — α . Когда по условию a → , n → ^ > 90 ° , тогда имеем a → , n → ^ = 90 ° + α .
Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы
cos a → , n → ^ = cos 90 ° — α , a → , n → ^ 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ > 90 °
Необходимо использовать формулы приведения для упрощения выражений. Тогда получим равенства вида cos a → , n → ^ = sin α , a → , n → ^ 90 ° cos a → , n → ^ = — s i n α , a → , n → ^ > 90 ° .
Проведя преобразования, система приобретает вид sin α = cos a → , n → ^ , a → , n → ^ 90 ° sin α = — cos a → , n → ^ , a → , n → ^ > 90 ° ⇔ sin α = cos a → , n → ^ , a → , n → ^ > 0 sin α = — cos a → , n → ^ , a → , n → ^ 0 ⇔ ⇔ sin α = cos a → , n → ^
Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.
Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле
sin α = cos a → , n → ^ = a → , n → ^ a → · n → = a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2
Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида
α = a r c sin a → , n → ^ a → · n → = a r c sin a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы cos α = 1 — sin α .
Выполним решение нескольких подобных примеров для закрепления материала.
Найти угол, синус, косинус угла, образованного прямой x 3 = y + 1 — 2 = z — 11 6 и плоскостью 2 x + z — 1 = 0 .
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что a → = ( 3 , — 2 , 6 ) является направляющим вектором прямой x 3 = y + 1 — 2 = z — 11 6 .
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости 2 x + z — 1 = 0 нормальный вектор имеет вид n → = ( 2 , 0 , 1 ) .
Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов a → и b → в заданную формулу. Получаем выражение вида
sin α = cos a → , n → ^ = a → , n → ^ a → · n → = a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2 = = 3 · 2 + ( — 2 ) · 0 + 6 · 1 3 2 + ( — 2 ) 2 + 6 2 · 2 2 + 0 2 + 1 2 = 12 7 5
Отсюда найдем значение косинуса и значение самого угла. Получим:
cos α = 1 — sin α = 1 — 12 7 5 2 = 101 7 5
Ответ: sin α = 12 7 5 , cos α = 101 7 5 , α = a r c cos 101 7 5 = a r c sin 12 7 5 .
Имеется пирамида, построенная при помощи значений векторов A B → = 1 , 0 , 2 , A C → = ( — 1 , 3 , 0 ) , A D → = 4 , 1 , 1 . Найти угол между прямой A D и плоскостью А В С .
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой A D направляющий вектор имеет координаты A D → = 4 , 1 , 1 .
Нормальный вектор n → , принадлежащий плоскости А В С , является перпендикулярным вектору A B → и A C → . Это подразумевает то, что нормальным вектором плоскости А В С можно считать векторное произведение векторов A B → и A C → . Вычислим это по формуле и получим:
n → = A B → × A C → = i → j → k → 1 0 2 — 1 3 0 = — 6 · i → — 2 · j → + 3 · k → ⇔ n → = ( — 6 , — 2 , 3 )
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:
α = a r c sin A D → , n → ^ A D → · n → = a r c sin 4 · — 6 + 1 · — 2 + 1 · 3 4 2 + 1 2 + 1 2 · — 6 2 + — 2 2 + 3 2 = a r c sin 23 21 2
💥 Видео
Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

ЕГЭ. ЦЭ. Угол между прямыми в пространствеСкачать

Как найти угол между плоскостямиСкачать

Урок 6. Угол между прямыми в пространстве. Стереометрия с нуля.Скачать

Угол между прямыми!Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

21. Угол между прямой и плоскостьюСкачать