О чем эта статья:
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Решение систем линейных уравнений с параметрами
- Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
- Угол наклона прямой и угловой коэффициент прямой
- Уравнение с угловым коэффициентом
- Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
- Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
- 📽️ Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:7 класс - Алгебра - Определение углового коэффициентаСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
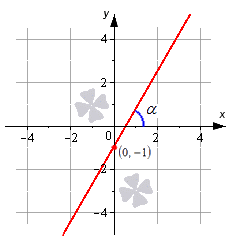
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Угловой коэффициент прямойСкачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
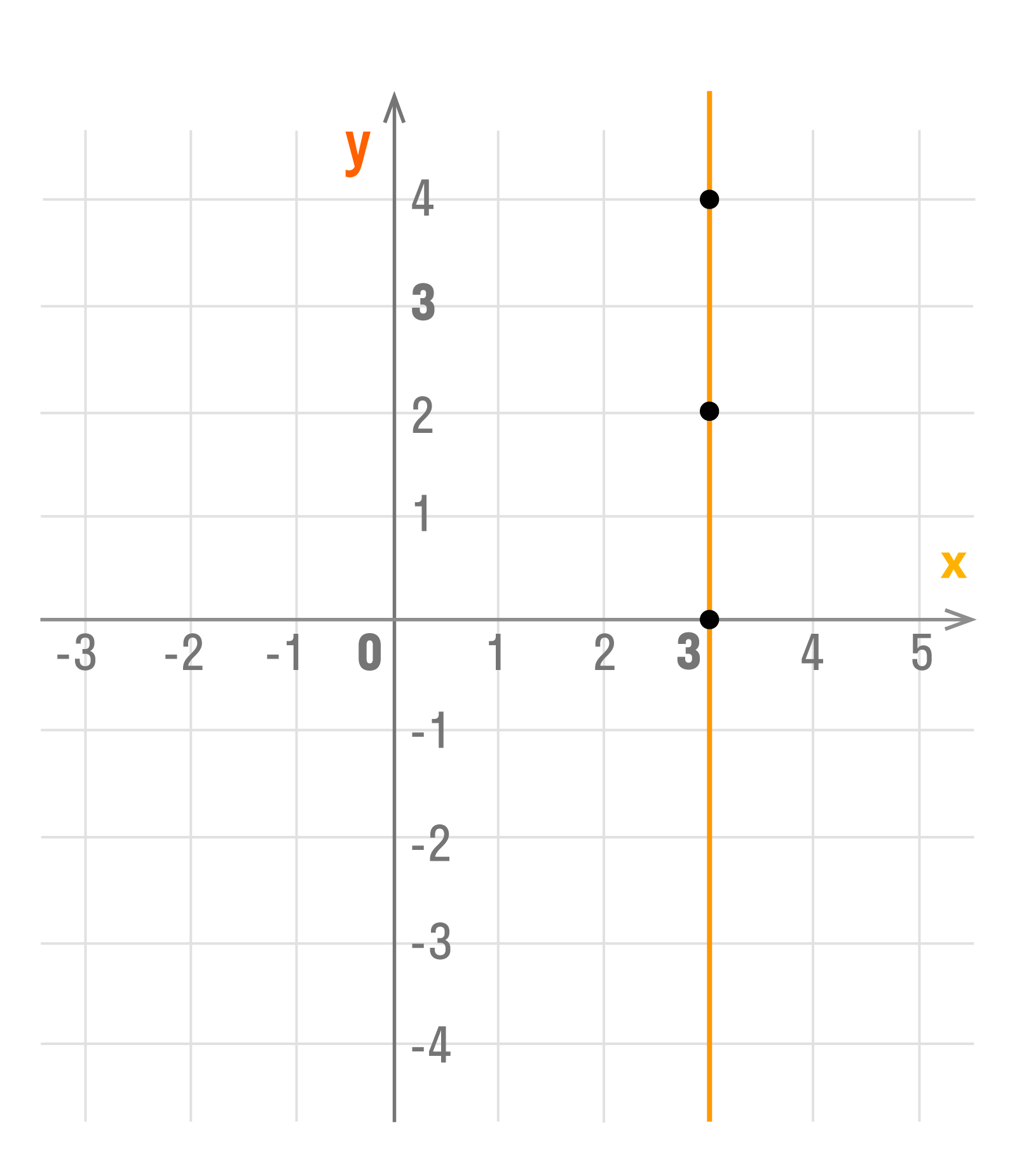
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Угловой коэффициент прямой. Решение задач.Скачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Решение систем линейных уравнений с параметрами
Разделы: Математика
Цель:
- повторить решение систем линейных уравнений с двумя переменными
- дать определение системы линейных уравнений с параметрами
- научит решать системы линейных уравнений с параметрами.
Ход урока
- Организационный момент
- Повторение
- Объяснение новой темы
- Закрепление
- Итог урока
- Домашнее задание
2. Повторение:
I. Линейное уравнение с одной переменной:
1. Дайте определение линейного уравнения с одной переменной
[Уравнение вида ax=b, где х – переменная, а и b некоторые числа, называется линейным уравнением с одной переменной]
2. Сколько корней может иметь линейное уравнение?
[- Если а=0, b
— Если а=0, b=0, то х 
— Если а
3. Выясните, сколько корней имеет уравнение (по вариантам)
| I ряд – I вариант |
Ответ: много корней
Ответ: корней нет
Ответ: единственный корень
II. Линейное уравнение с 2 –мя переменными и система линейных уравнений с 2- мя переменными.
1. Дайте определение линейного уравнения с двумя переменными. Приведите пример.
[Линейным уравнением с двумя переменными называются уравнения вида ах +by=с, где х и у – переменные, а, b и с – некоторые числа. Например, х-у=5]
2. Что называется решением уравнения с двумя переменными?
[Решением уравнения с двумя переменными называются пара значений переменных, обращающие это уравнение в верное равенство.]
3. Является ли пара значений переменных х = 7, у = 3 решением уравнения 2х + у = 17?
4. Что называется графиком уравнения с двумя переменными?
[Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых является решениями этого уравнения.]
5. Выясните, что представляет собой график уравнения:
[Выразим переменную у через х: у=-1,5х+3
Формулой у=-1,5х+3 является линейная функция, графиком которой служит прямая. Так как, уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6]
6. Что является графиком уравнения ах+bу=с с переменными х и у, где а

[Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.]
7. Что называется решением системы уравнений с двумя переменными?
[Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство]
8. Что значит решить систему уравнений?
[Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.]
9. Выясните, всегда ли имеет такая система решения и если имеет, то сколько (графическим способом).
10. Сколько решений может иметь система двух линейных уравнений с двумя переменными?
[Единственное решение, если прямые пересекаются; не имеет решений, если прямые параллельны; бесконечно много, если прямые совпадают]
11. Каким уравнением обычно задается прямая?
12. Установите связь между угловыми коэффициентами и свободными членами:
I вариант:
|
k1 = k2, b1
- y=-х+8
- y=2x-1,
k1
- y=-x-1
- y=-x-1,
k1 = k2, b1 = b2, много решений.
Вывод:
- Если угловые коэффициенты прямых являющихся графиками этих функций различны, то эти прямые пересекаются и система имеет единственное решение.
- Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые параллельны, а система не имеет решений.
- Если угловые коэффициенты и точки пересечения с осью у одинаковы, то прямые совпадают и система имеет бесконечно много решений.
На доске таблица, которую постепенно заполняет учитель вместе с учениками.
III. Объяснение новой темы.
где A1, A2, B1,B2, C1 C2 – выражения, зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.
Возможны следующие случаи:
1) Если 
2) Если 
3) Если 
IV. Закрепление
Пример 1.
При каких значениях параметра а система
- 2х — 3у = 7
- ах — 6у = 14
а) имеет бесконечное множество решений;
б) имеет единственное решение
а) 
б) 
а) если а=4, то система имеет бесконечное множество решений;
б) если а
Пример 2.
Решите систему уравнений
- x+(m+1)y=1
- x+2y=n
Решение: а) 

б) 

в) 
Ответ: а) если m=1 и n
б) m=1 и n=1, то решение бесконечное множество
- у — любое
- x=n-2y
в) если m
y= 
Пример 3.
Для всех значений параметра а решить систему уравнений
- ах-3ау=2а+3
- х+ау=1
Решение: Из II уравнения найдем х=1-ау и подставим в I уравнение
1) а=0. Тогда уравнение имеет вид 0*у=3 [у 
Следовательно, при а=0 система не имеет решений
Следовательно, у 
3) а



1) если а=0, то (х; у)
2) если а=-3, то х=1+3у, у
3) если а
Рассмотрим II способ решения системы (1).
Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В2, второе на – В1 и сложим почленно эти уравнения, исключив, таким образом, переменную у:
Т.к. А1В2-А2В1
т.к. А2В1-А1В2 
Для удобства решения системы (1) введем обозначения:

Теперь решение системы (1) можно записать с помощью определителей:
х= 
Приведенные формулы называют формулами Крамера.
— Если 

— Если 



— Если 



В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае 

Если коэффициенты А1, А2, В1, В2, системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.
Пример 4.
Для всех значений параметра а решить систему уравнений
- (а+5)х+(2а+3)у=3а+2
- (3а+10)х+(5а+6)у=2а+4
Решение: Найдем определитель системы:






1) 
х= 
2) 
При а=0 определители
Тогда система имеет вид:
- 5х+3у=2
5х+3у=2
- 10х+6у=4
При а=2 
1) если а 


2) если а=0, то х
3) если а=2, то (х; у)
Пример 5.
Для всех значений параметров а и b решить систему уравнений
Решение: 









1) 
х= 
2)
Подставив выражение параметра а в систему, получим:
- 2bx+2y=b 2bx+2y=b
- bx+y=3
2bx+2y=6
Если b
Если b=6, а=2b-1=2*6-1=11, то система равносильна одному уравнению
12х+2у=6 
1) если 


2) если b

3) если b=6, а=11, то х
Итог урока: Повторить по таблице и поставить оценки.
При каких значениях параметра система уравнений
- 3х-2у=5
- 6х-4у=b
а) имеет бесконечное множество решений
б) не имеет решений
б) b
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
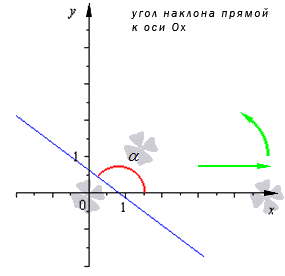
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Видео:Угловой коэффициент прямойСкачать

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Видео:Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
📽️ Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Угловой коэффициент прямой. Пример 1Скачать
Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Угловой коэффициент прямой. Пример 3Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Алгебра 7. Урок 8 - Системы линейных уравненийСкачать

Урок 67. Системы линейных уравненийСкачать






















 5х+3у=2
5х+3у=2 






 2bx+2y=6
2bx+2y=6