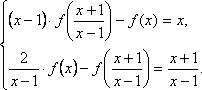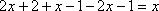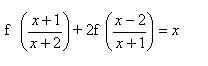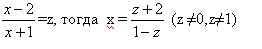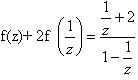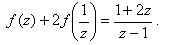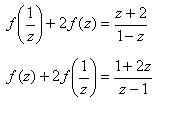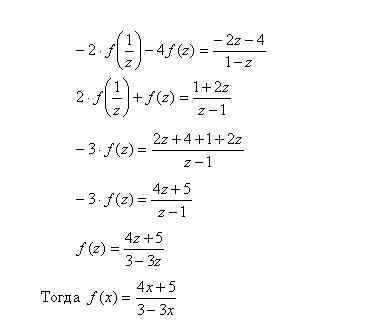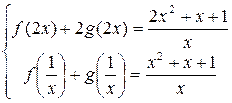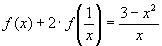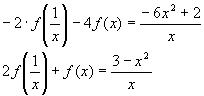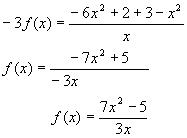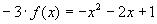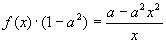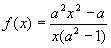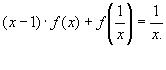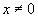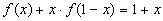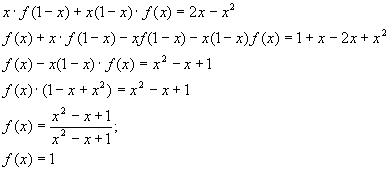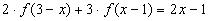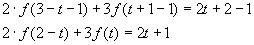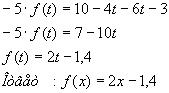Удовлетворяет ли заданное уравнение функции (2 видео)

Решение функциональных уравнений методом подстановки

Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.

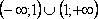
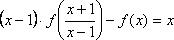
1. Найдите все функции, определённые на множестве , удовлетворяющие соотношению .

Решение:

Придадим x значение . Получим

Отсюда .

Получим систему

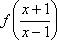
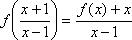
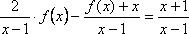
Из уравнения (1) выразим и подставим в уравнение (2).

; ;

Отсюда ;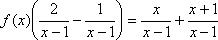

;

Проверим, действительно ли функция f(x) удовлетворяет уравнению .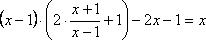

Ответ: .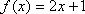

2. Найти функцию, удовлетворяющую уравнению

Решение:

2) Подставим в исходное уравнение, получим

3)Заменим z на 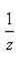получим

или после преобразований в правой части уравнения:

4)Итак, получили два уравнения:

5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:

3.Пусть 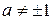— некоторое действительное число. Найти функцию f(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению

,где g – заданная функция, определённая при x ≠ 1.

Решение:При замене

получаем систему

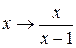
решением которой при a 2 ≠ 1 является функция

Ответ:

4.Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):

Решение:

В первом уравнении сделаем подстановку 2x = 1/z.

и первое уравнение принимает вид:

или

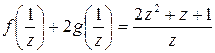
В результате получаем систему уравнений:

решение которой g(x) = 1/x, f(x) = x+1.

Ответ:g(x) = 1/x, f(x) = x+1.

5.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у. (1)

Решение:

Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.

Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у ? R.

6.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у. (2)

Решение:

Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.

7.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению

f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)

Решение:

Поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (3) получаем f(х)= х 2 -х+1 .

Ответ: f(х)= х 2 -х+1.

8.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению

f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (4)

Решение:

Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х 2 +6х+6)у=0 относительно х получаем х₁= -1, х₂= -5. Подстановка любого из этих значений в (4) дает нам f(у)=у 2 -4у.

9.Решите следующие функциональные уравнения.

в) f(x+y)+f(x-y)=2f(x)cos y

Решение:

а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.

б) Положим y=x-1/x , затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим

в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= — f(x). Заменив у на у+π/2, получаем

заменив теперь х- π/2 на х, имеем:

и с учетом предыдущего:

Положив х=0, получаем отсюда и из исходного уравнения:

Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.

10.

Решение: 1) Заменим на , получим или .

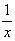
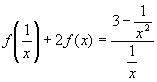
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

11. 2

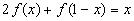
Решение: 1)Заменим в уравнении на , получим 2 .

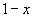
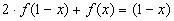
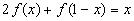
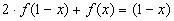
2) Умножим обе части исходного уравнения 2 на (-2) и сложим с уравнением 2 ,

получим:

12.

Решение:

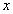
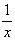
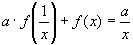
1) Заменим в уравнение на , .

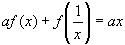
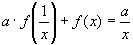
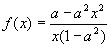
2)Умножим уравнение на и вычтем из уравнения , получим —

, где а

13.

Решение:

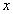
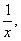
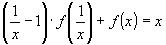
1)Заменим в уравнении на получим .

2)Выразим из исходного уравнения 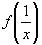, получим

или .

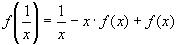
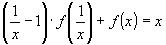
3)Подставим в уравнение , получим .

14.

Решение:

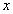
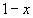
1.Заменим на , получим

2.Умножим обе части уравнения на и вычтем из уравнения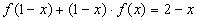

15.

Решение:1)Пусть 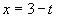, тогда уравнение принимает вид:

2)Пусть 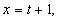тогда исходное уравнение принимает вид:

3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:

16.

Решение:

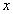
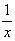
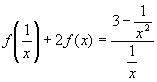
1) Заменим на , получим или .

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

Видео:21. Частные производные второго порядка. Часть 4.Скачать

Электронная библиотека

Пример 1. Проверить удовлетворяет ли указанному уравнению данная функция z = f(x,y).

Решение. Находим частные производные первого и второго порядка:

Подставляем полученные значения производных в левую часть исходного уравнения:

В правой части уравнения имеем:

Сравнивая полученные результаты, видим, что данная функция удовлетворяет исходному уравнению.

Пример 2. Вычислить приближенно данные выражения, заменив приращения соответствующих функций их полными дифференциалами. Оценить в процентах возникающую при этом относительную погрешность вычислений.

Решение. а) Рассмотрим функцию

Значение этой функции в точке известно и равно

Вычислим приближенно значение функции по формуле:

Видео:показать, что функция удовлетворяет соотношениюСкачать

Функциональные уравнения. Методы их решения

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Министерство образования и молодежной политики Чувашской Республики

БОУ ДПО (ПК) С «Чувашский республиканский институт образования»

Кафедра математики и информационных технологий

Курсовая работа на тему:

« Функциональные уравнения. Методы их решения»

Выполнил (а): учитель математики МБОУ «СОШ № 60»

Глава 1. Понятие функционального уравнения ………………………………. 5

Глава 2. Практическая часть. Методы решения функционального уравнения.9

Одно из важнейших математических умений, которым должны овладеть учащиеся школы, — умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, в уравнении могут участвовать целые, рациональные и другие числа, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение, решать, которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.

Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование. функциональный уравнение коши

Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе. Так как эта тема в школьном курсе не изучается в виду её сложности, при поступлении в престижные ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.

В настоящее время практически нет никаких пособий, обучающих решению функциональных уравнений.

Поэтому ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов решения функциональных уравнений.

Цель работы — выяснить, что является функциональным уравнением их системами, найти способы решения и составить сборник задач для использования математическими классами.

1. изучение и анализ литературы;

2. поиск способов решения функциональных уравнений и их систем;

3. решение функциональных уравнений

4. составление сборника

Объект исследования: функциональные уравнения

Предмет исследования: изучение свойств и способов решения функциональных уравнений.

Структура: введение, понятие функционального уравнения, сборник задач, заключение.

Глава 1. Понятие функционального уравнения

Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют. Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях.

Некоторые функциональные уравнения знакомы нам еще из школьного курса это

которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

(1)

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

этого уравнения, предполагая только непрерывность f(x).

Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

, (2)

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

(3)

Функциональному уравнению (3) удовлетворяют, в частности, функции:

Одними из простейших функциональных уравнений являются уравнения Коши

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид

, , ,

В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.

Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение — значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax . Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) — непрерывна, то это действительно так, если же данное предположение отбросить — то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.

Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) — класс функций, симметричных относительно прямой x = 1 , и т. д.