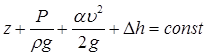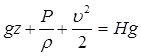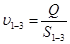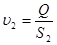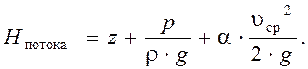Определения
Элементарная струйка – струйка жидкости, боковая поверхность которой образована линией тока, проходящей через бесконечно малый замкнутый контур. Распределение скоростей по поперечному сечению элементарной струйки считается равномерным, по причине малости площади поперечного сечения, поэтому коэффициент Кориолиса 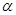
Идеальная жидкость – модель жидкости, применяемая для расчётов реальных гидродинамических процессов.
Для идеальной жидкости приняты следующие допущения:
· отсутствуют касательные напряжения между слоями жидкости, следовательно,
отсутствует вязкость жидкости, следовательно, отсутствует трение между слоями жидкости, следовательно, в жидкости отсутствуют потери напора;
· жидкость является не сжимаемой;
· в жидкости отсутствует теплопроводность, т.е. жидкость не изменяет свой объём при изменении температуры;
· поток жидкости является сплошным, т.е. в жидкости отсутствуют места пустот или переуплотнений.
Виды уравнения Бернулли
Для элементарной струйки идеальной жидкости
Для элементарной струйки коэффициент Кориолиса равен единице, в идеальной жидкости отсутствуют потери, поэтому уравнение Бернулли будет иметь вид:
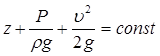
Для потока реальной жидкости
Для потока жидкости коэффициент Кориолиса будет иметь значение отличное от единицы, и зависеть от режима течения, для ламинарного режима α = 2, для турбулентного режима α = 1,05-1,1. Реальная жидкость имеет вязкость, следовательно, в реальной жидкости будут потери напора, поэтому уравнение Бернулли будет иметь вид:
Геометрический смысл уравнения Бернулли
Рассмотрим уравнение Бернулли для элементарной струйки идеальной жидкости (1).
В уравнении (1) все три слагаемых имеют линейную размерность [м]. Соответственно каждую высоту можно представить в виде реальных отрезков:


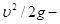
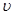
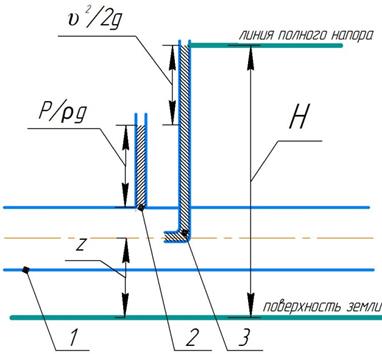
Рис. 1 Иллюстрация геометрического смысла уравнения Бернулли.
1 – элементарная струйка; 2 – пьезометр; 3 – трубка Пито (прибор для измерения скоростной высоты).
Геометрический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх слагаемых уравнения Бернулли остаётся величиной постоянной и равной величине полного напора Н [м].

Энергетический смысл уравнения Бернулли
Умножим каждое слагаемое уравнения (2) на величину ускорения свободного падения:
В итоге получаем слагаемые, который можно описать с точки зрения энергии:
где 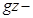


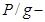

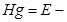
Энергетический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх удельных энергий остаётся величиной постоянной и равной величине полной удельной механической энергии Е [Дж]. Возможна и другая формулировка: уравнение Бернулли – это есть закон сохранения энергии для элементарной струйки (потока) жидкости, который отображает взаимный переход кинетической и потенциальной энергии.
Потери
В потоке реальной жидкости в уравнение Бернулли добавляется слагаемое 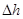
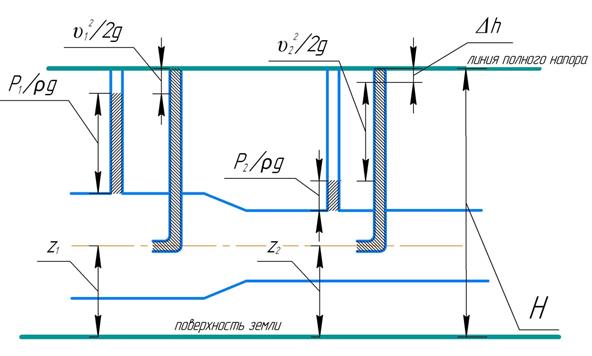
представляет собой величину потерь напора. Запишем уравнение Бернулли для двух произвольных сечений потока жидкости:
С геометрической точки зрения потери отображаются отрезком, расположенным над скоростным напором, при этом потери отображаются во втором сечении.
Рис. 2. Иллюстрация потерь напора.
С энергетической точки зрения 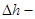
6. Порядок проведения расчётов:
1. Определить величину расхода жидкости:
2. Поскольку диаметры d1=d3, дальнейшие расчёты для широких частей трубопровода будут одинаковы. Поэтому будем проводить расчёт для одной широкой части трубопровода, при этом параметры жидкости, обозначая через индекс 1-3
Определить площади поперечного сечения трубопроводов S1-3, S2 [м];
3. Определить скорость течения жидкости:
4. Определить режим течения жидкости:
5. Определить величины скоростного напора: 
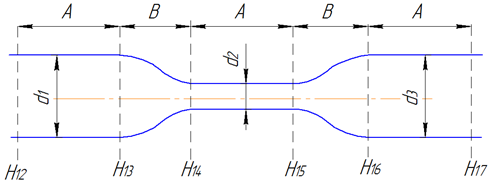
6. На листе А4 построить график, зависимости изменения пьезометрического напора от
длины сечения трубопровода.По оси Х откладываются расстояния между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см
Рис. 3 Условное изображение исследуемого
трубопровода с точками подключения пьезометров.
По оси Y откладываются показания соответствующих пьезометров. В результате получится шесть точек, который соединяются ломаной линией. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.
7. На листе А4 построить график, зависимость изменения скоростного напора от длины
сечения трубопровода.По оси Х откладывается расстояние между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см.
По оси Y откладываются значения скоростного напора. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.
8. Вывод о работе с описанием графиков
Таблица 1. Результаты опыта
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли
Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Уравнение Бернулли выглядит так:
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.
Содержание статьи
Видео:Закон БернуллиСкачать

Смысл уравнения Бернулли
По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.
Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.
В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.
Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.
Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную
Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.
В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.
Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.
Отсюда следует, что между напором и удельной энергией существует очень простая зависимость
где э – удельная энергия
Уравнение Бернулли для элементарной струйки реальной жидкости
Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.
При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет
Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается
Величина Э1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.
Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.
В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.
Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.
Слагаемое h1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— hлп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— hмп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости
Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.
Видео:Уравнение Бернулли гидравликаСкачать

Энергетическая интерпретация уравнения Бернулли
Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости
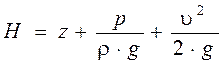
Физический смысл слагаемых, входящих в уравнение следующий:
ü z –удельная потенциальная энергия положения – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;
ü 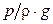
ü 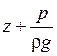
ü 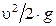
ü 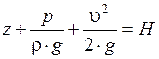
3.7Уравнение Бернулли для потока идеальной жидкости
Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока) (рисунок 3.4). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек υS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока υ, будет иметь разные значения.
Вводят коэффициент кинетической энергии или коэффициента Кориолисаα.Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.
Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:
Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения. При ламинарном режиме движения a=2; при развитом турбулентном режиме a=1,05 ¸ 1,1. Для большинства технических задач обычно принимается a=1.
3.8 Уравнение Бернулли для потока реальной (вязкой) жидкости
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят
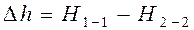
где 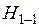
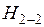
В этом случае уравнение Бернулли будет иметь вид
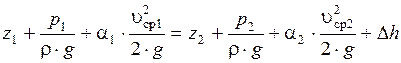
3.9Разность напоров и потери напора
Различие в применении терминов «разность напоров» и «потери напора»с одним и тем же обозначением Δh поясним на примерах.
Движение жидкости происходит только при наличии разности напоров(Δh = H1— H2), от точки с большим напором H1к точке с меньшим H2. Например, если два бака, заполненных водой до разных высотных отметок, соединить трубопроводом, то по нему начнётся перетекание в бак с меньшей отметкой уровня воды под влиянием разности напоров Δh, равной в этом случае разности отметок уровней воды в баках. При выравнивании уровней напоры в обоих баках становятся одинаковыми H1= H2, разность напоровΔh=0 и перетекание прекращается.
Потери напора Δh отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (Δh = 0), однако разность уровней воды будет создавать некоторую разность напоровΔh. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках Δh = H1— H2, то есть мы опять пришли к уравнению Бернулли.
Таким образом, «разность напоров»является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.
Обычно в гидравлических задачах при известных скорости 

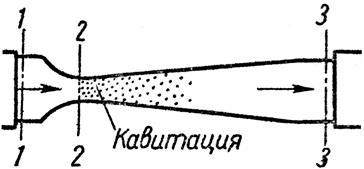
3.10Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходят явления, связанные с изменением агрегатного состояния жидкости, т. с. с превращением ее в пар, а также с выделением из жидкости растворенных в ней газов. Например, при течении жидкости через местное сужение трубы (сечение 2-2) (рисунок 3.8) увеличивается скорость и падает давление согласно уравнению Бернулли
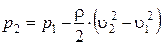
Рисунок 3.8 – Возникновение кавитации
Если абсолютное давление при этом достигает значения, равного давлению насыщенных паров этой жидкости при данной температуре, или давлению, при котором начинается выделение из нее растворенных газов, то в данном месте потока начинается интенсивное парообразование (кипение) и выделение газов. В расширяющейся части (сечение 3-3) скорость потока уменьшается, а давление возрастает, и выделение паров и газов прекращается; выделившиеся пары конденсируются, а газы постепенно вновь растворяются. Эта труба переменного сечения называется трубой Вентури, которая сначала плавно сужает поток, затем еще более плавно расширяет.
Это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке, называется кавитацией.
Размеры зоны кавитации возрастают по мере увеличения скорости потока жидкости т. е. при увеличении давления в сечении 1-1, а следовательно, и расхода. Но давление в узком сечении 2-2 постоянно, потому, что постоянно давление насыщенных паров.
Кавитация сопровождается характерным шумом и вибрациями, а при длительном ее воздействии также эрозионным разрушением металлических стенок. Последнее объясняется тем. что конденсация пузырьков пара (и сжатие пузырьков газа) происходит со значительной скоростью, частицы жидкости, заполняющие полость конденсирующегося пузырька, устремляются к его центру и в момент схлопывания пузырька вызывают местные удары, т. е. значительное повышение давления в отдельных точках. Материал при кавитации разрушается не там, где выделяются пузырьки, а там, где они конденсируются. Это явление называется кавитационным износом.
При возникновении кавитации значительно увеличивается сопротивление трубопроводов и, следовательно, уменьшается их пропускная способность, потому что каверны уменьшают живые сечения потоков, скорость в которых резко возрастает.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Она может возникать во всех местных гидравлических сопротивлениях, где поток претерпевает местное сужение с последующим расширением, например в кранах, вентилях, задвижках, диафрагмах, жиклерах и др. В отдельных случаях возникновение кавитации возможно также и без расширения потока вслед за его сужением, а также в трубах постоянного сечения при увеличении геометрической высоты и гидравлических потерь.
Кавитация возникает не только при движении жидкости в трубопроводе, но и при внешнем обтекании тел, в частности, на лопастях гребных винтов, рабочих колес насосов и гидравлических турбин.
Для оценки режима течения жидкости в каком-либо сечении потока вводят специальный критерий – число кавитации
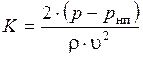
где p,υ — давление и средняя скорость течения жидкости в данном сечении потока.
3.11Моделирование гидродинамических явлений
Существует два различных метода моделирования:
— физическое моделирование, т.е. на модели воспроизводится изучаемое явление с сохранением его физических свойств;
— математическое моделирование, т.е. исследование натурных состояний или процессов выполняется путем изучения явлений, имеющих иное физическое содержание, но описываемое теми же математическими зависимостями.
Кроме того следует различать две разных категории моделей:
— воображаемые или мысленные, которые не полностью отражают действительность и могут быть также названы идеальными телами или процессами. Эти модели исследуются теоретически и результаты их исследования могут быть применены к реальности с помощью поправочных коэффициентов. Эти модели могут быть описаны чертежами, словами или математическими знаками.
— материальные, которые воспроизводят в определенном масштабе конструкции или процессы, имеющие место в действительности. Эти модели могут быть воспроизведены в лаборатории или в полевых условиях.
Оба видов моделей могут относиться и к математическому и физическому моделированию.
В дальнейшем понятие моделирование будет относиться к «материальному физическому» моделированию.
В процессе проектирования различных гидросистем, трубопроводов, гидротехнических сооружений, гидравлических и газовых систем нередко возникает необходимость не только математического, но и натурного моделирования. В таком случае необходимо, чтобы работа гидросистемы действующей модели соответствовала функционированию реального объекта. Это означает, что различные характеристики потоков жидкости, которые имеют место в модели и в реальной системе, должны описываться одинаковыми закономерностями, хотя их численные значения могут существенно различаться. В натурной модели они меньше (как правило) или больше (встречается реже), чем в действительности. Для этого необходимо иметь критерии, которые позволяли ли бы «масштабировать» реальную систему. Эти критерии устанавливаются в теории подобия потоков жидкости.
Представим себе две геометрически подобные фигуры (рисунок 3.9). Сходственными точками этих фигур называются точки, одинаково расположенные по отношению к границам этих фигур. Причем в сходственных точках фигур на частицы жидкости (сплошной среды) действуют силы одной физической природы.
Рисунок 3.9 – Подобные потоки жидкости
Гидродинамическое подобие— это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.
Геометрическое подобие означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, т.е. подобие русел или трубопроводов, по которым течёт жидкость.
Например, для двух трубопроводов: 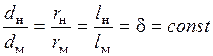
где δ – линейный масштаб подобия.
Кинематическоеподобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.
Например, для вращающегося движущегося тела
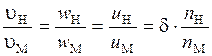
Т.о. кинематически подобные системы всегда будут геометрически подобными.
Динамическое подобие заключается в пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил.
Т.е. можно сказать, что динамически подобными системами будут такие, для которых векторные поля сил, действующих на жидкость, образованы одноименными силами, причем эти поля будут геометрически подобными и одинаково ориентированы относительно границ систем.
В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.
На практике полное гидродинамическое подобие достигается редко, поэтому обычно ограничиваются частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.
Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде
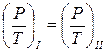
3.12Теория ламинарного и турбулентного движения жидкости
3.12.1Режимы течения жидкости в трубах
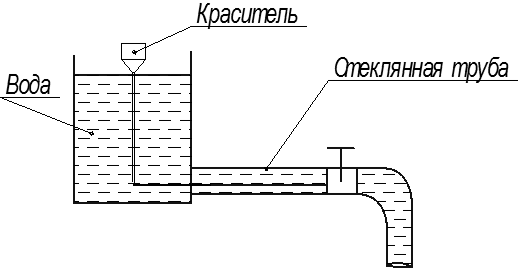
Еще в середине XIX века в результате опытов Гагена (1838 г.), Пуазейля (1841 г.) было установлено, что существуют два принципиально различных режима течения жидкости. Наиболее полно этот вопрос исследовал О.Рейнольдс (1883 г.). Различные режимы течения жидкости можно наблюдать вводя в поток подкрашивающую струйку красителя (рисунок 3.10).
Рисунок 3.10 – Схема установки О. Рейнольдса.
Замечено, что при небольшой скорости воды струйка красителя вытягивается в тонкую нить, которая, не размываясь, достигает конца трубы. Это свидетельствует о том, что пути частиц прямолинейны и параллельны друг другу.
Режим движения, при котором поток жидкости движется параллельно, скользящими друг относительно друга слоями или струйками, называется ламинарным. При этом режиме слои потока жидкости между собой не перемешиваются и движение происходит без пульсаций скорости. Ламинарный режим можно наблюдать в капиллярных трубках при движении вязких жидкостей типа нефти, мазута, сахарного сиропа и т. д.
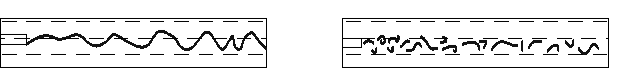
Если скорость воды в трубе увеличивать сверх определенного предела, то окрашенная струйка сначала приобретает волнообразное движение (рисунок 3.11), а затем начинает размываться, смешиваясь с водой. Такое неоднородное движение, при котором отдельные частицы жидкости движутся по беспорядочным, хаотическим траекториям, налагающимся на осредненное движение, называется турбулентным. В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению.
Переход ламинарного режима в турбулентный происходит при определённой средней скорости течения υср, которая зависит от диаметра трубы и вязкости жидкости. Эту скорость называют критической и определяют по формуле
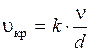
где 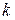
Т.е. изменение режима течения происходит при определённом соотношении между скоростью, диаметром и вязкостью ν
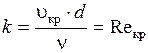
Полученное безразмерное число называется критическим числом Рейнольдса. С физической точки зрения число Рейнольдса есть отношение сил инерции потока к силам трения.
Опытным путём установлено, что критическое число Рейнольдса для круглых труб — 2320для круглых труб, а для других сечений 580.
Для определения режима движения в потоке надо найти фактическое число Рейнольдса Re , которое можно установить для любого потока по формуле
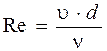
и сравнить его с критическим числом Reкр.
При движении жидкости в прямых круглых трубах на участках, достаточно удаленных от входа, и при отсутствии различных возмущающих условий установлено, что
¾ при Re 2320 – режим движения жидкости – турбулентный.
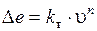
где kт и kл – коэффициенты пропорциональности (сопротивления трубопровода).
Различие между ламинарным и турбулентным режимами имеется также и в распределении скоростей в живом сечении потока.
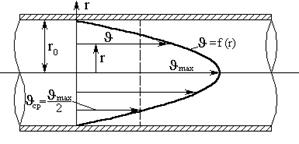
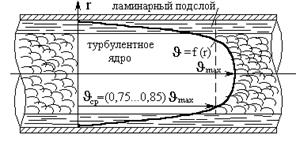
При ламинарном режиме распределение скорости по сечению имеет параболический закон (рисунок 3.12, а); при турбулентном режиме закон распределения более сложный (рисунок 3.12, б).
Рисунок 3.12 – Распределение скорости в поперечном сечении трубы при ламинарном и турбулентном режиме движения жидкости.
🎬 Видео
Уравнение БернуллиСкачать

Уравнение Бернулли для потока жидкостиСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Гидравлика 09 Уравнение бернуллиСкачать

Закон БернуллиСкачать

Эффект Магнуса и уравнение БернуллиСкачать

Клапан Тесла | Целая физикаСкачать

Дистанционная работа 5 - иллюстрация уравнения БернуллиСкачать

BERNOULLY[Уравнение Бернулли]Скачать
![BERNOULLY[Уравнение Бернулли]](https://i.ytimg.com/vi/GMbJx7Ye5Po/0.jpg)
Урок гидравлики - 01 - Основные положенияСкачать

Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Уравнение Бернулли для общей энергииСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Закон Бернулли и движение по инерцииСкачать

Вывод уравнения БернуллиСкачать

Парадокс сужающейся трубыСкачать