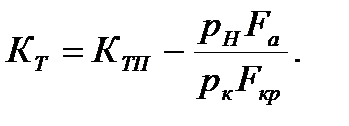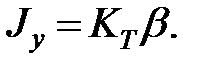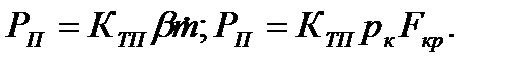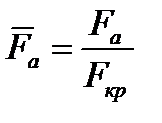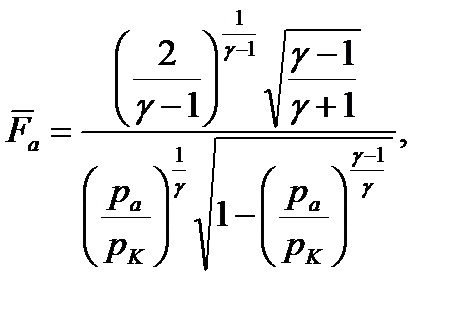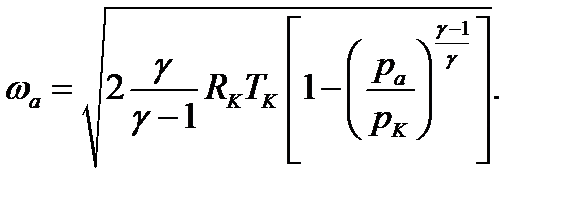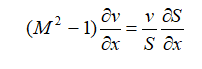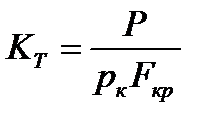
Коэффициент тяги показывает увеличение тяги двигателя вследствие наличия сопла. Иногда КТ называют безразмерной тягой. Теоретическое значение КТ рассчитывается по полученному из формулы тяги выражению
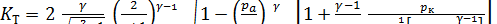
Условно коэффициент тяги можно представить в виде
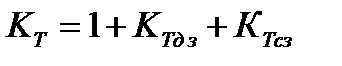
где 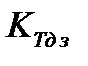
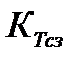
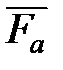
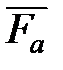
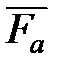
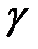
Для анализа удобнее использовать коэффициент тяги в пустоте
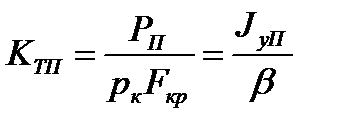
Расчетное выражение для КТП получается из (2.9) при pн =0

Очевидно, что КТП не зависит ни от работы камеры сгорания, ни от внешних условий (рн) и является характеристикой, определяющей только работу сопла камеры.
Коэффициенты КТ и КТП связаны между собой зависимостью
В заключение следует отметить, что для определения 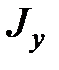
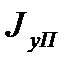
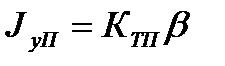
2.2.5. Геометрическая степень расширения сопла
Эта величина не только определяет размеры сопла, но и характеризует основные параметры работы сопла: 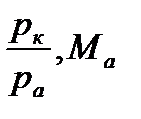
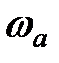
Таким образом, РД имеет 5 основных показателей, нужных для создания ракеты:
тяга 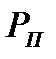
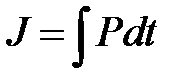
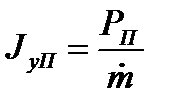
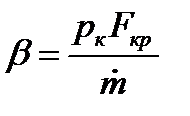
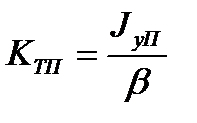
2.2.6. Удельная масса ракетного двигателя
Также существует такой важный для любой подсистемы ЛА показатель, как масса конструкции РД. Удельной массой двигателя называют отношение его массы в рабочем состоянии к развиваемой наибольшей тяге на основном режиме работы. Это определение справедливо только для ЖРД, так как массу РДТТ трудно отделить от массы ракеты.
Рабочим считают состояние ЖРД, при котором магистрали и агрегаты двигателя заполнены компонентами топлива, и масса двигателя составляет МД. По определению 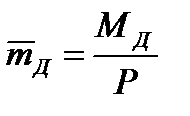
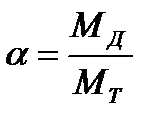
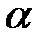
Видео:ОГЭ. Физика. Определение выталкивающей (архимедовой) силыСкачать

Расчёт сопел современных ракетных двигателей
Введение
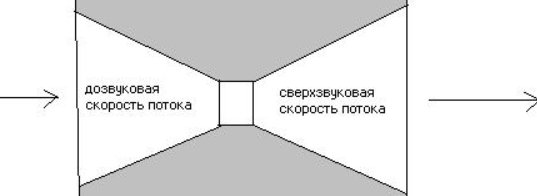
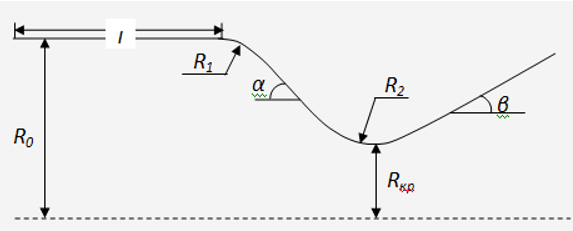
Сопло ракетного двигателя- техническое приспособление, которое служит для ускорения газового потока, проходящего по нему до скоростей, превышающих скорость звука. Основные виды профилей сопел приведены на рисунке:
По причине высокой эффективности ускорения газового потока, нашли практическое применение сопла Лаваля. Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами:
В ракетном двигателе сопло Лаваля впервые было использовано генералом М. М. Поморцевым в 1915 году. В ноябре 1915 года в Аэродинамический институт обратился генерал М. М. Поморцев с проектом боевой пневматической ракеты.
Ракета Поморцева приводилась в движение сжатым воздухом, что существенно ограничивало ее дальность, но зато делало ее бесшумной. Ракета предназначалась для стрельбы из окопов по вражеским позициям. Боеголовка оснащалась тротилом.
В ракете Поморцева было применено два интересных конструктивных решения: в двигателе имелось сопло Лаваля, а с корпусом был связан кольцевой стабилизатор. Подобные конструкции используются и в настоящее время, но уже с твёрдотопливным двигателем и системой автоматического наведения:
Однако проблемы остались старые, но уже в современном исполнении: ограниченная дальность до 3 км., наведение и удержание цели в условиях хорошей видимости, что для настоящего боя не реально, не защищённость от электромагнитных заградительных помех и, наконец, но не в последнюю очередь, высокая стоимость.
Теоретические основы
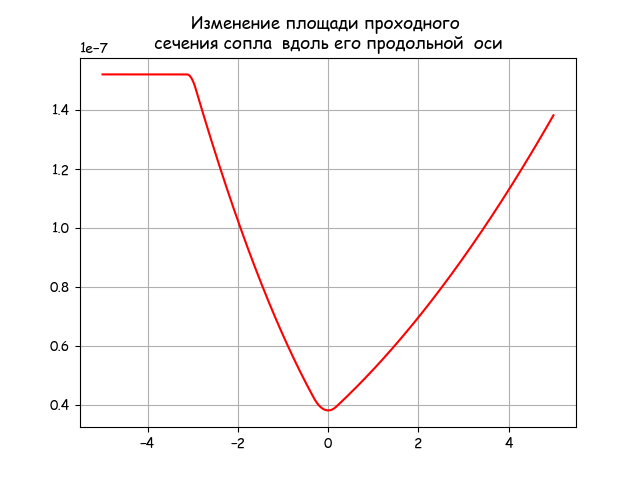
Эффективные сопла современных ракетных двигателей профилируются на основании специальных газодинамических расчётов. Основное уравнение, связывающее градиент площади сечения, градиент скорости и число Маха, следующее:
где: S – площадь сечения сопла; v – скорость газа; M – число Маха (отношение скорости газа в какой-либо точке потока к скорости звука в этой же точке).
Анализируя это соотношение, получаем, что в сопле Лаваля могут осуществляться следующие режимы течения:
1) M 0 (из уравнения). Дозвуковой поток в сужающемся канале ускоряется.
б) 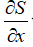
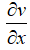
а) 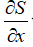
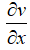
3) 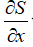
Тогда возможно либо М = 1 (поток переходит через скорость звука), либо 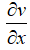
Какой из режимов реализуется на практике, зависит от перепада давлений между входом в сопло и окружающей средой.
Если давление, достигаемое в критическом сечении, превышает наружное давление, то поток на выходе из сопла будет сверхзвуковым. В противном случае он остается дозвуковым. [2]
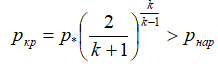
где: p* – давление торможения (давление в камере); pкр – давление в критическом сечении сопла; pнар – давление в окружающей среде; k – показатель адиабаты.
Если известны параметры в камере сгорания, то параметры в любом сечении сопла можно узнать по следующим соотношениям:
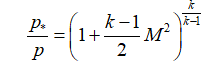
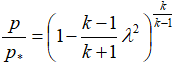
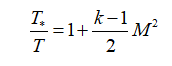

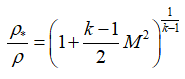
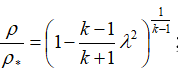
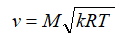
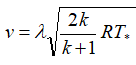
В этих формулах – λ – приведенная скорость, отношение скорости газа в данном сечении сопла к скорости звука в критическом сечении, R – удельная газовая постоянная. Индексом «*» обозначены параметры торможения (в данном случае – параметры в камере сгорания).
Постановка задачи
1. Рассчитать параметры течения потока газов в сопле Лаваля: для этого профиль сопла Лаваля разбивается на 150 контрольных точек – 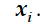
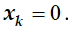
2. Расчёты выполнить средствами высокоуровневого свободно распространяемого языка программирования Python по следующей расчётной схеме и исходным данным:
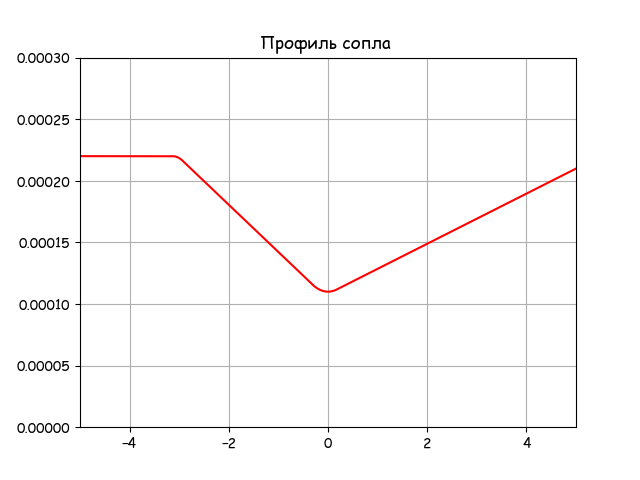
Рисунок 1-Профиль сопла Лаваля
Таблица 1-Исходные данные
Приведенные исходные данные носят демонстрационный характер.
Расчёт сопла Лаваля средствами Python
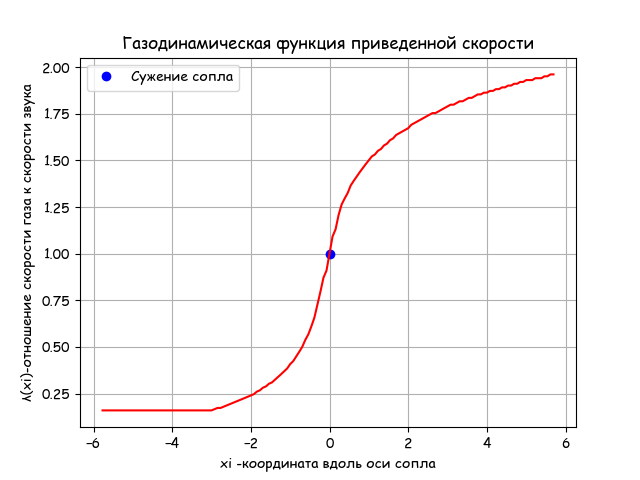
Для продолжения решения задачи на Python, нужно связать λ – приведенную скорость газа с координатой x вдоль продольной оси. Для этого я воспользовался функцией fsolve из библиотеки SciPy со следующей инструкцией:
fsolve( , ,xtol=1.5 · 10^8)
Привожу фрагмент программы для управления решателем с одной стартовой точкой:
Это единственно возможное на Python решение сложного алгебраического уравнения со степенной функцией от показателя адиабаты k. Например, даже для упрощённого уравнения с использованием библиотеки SymPy, получим недопустимое время расчёта только одной точки:
Время работы решателя: 195.675
0.16
1.95
Время работы программы: 0.222
Полученная эпюра распределения скоростей газового потока полностью соответствует изложенной выше теории. При этом, по предложенному алгоритму и библиотеке, время расчёта в 150 точках в 1000 раз меньше, чем для одной точки с использованием solve sympy.
Время работы программы: 0.203
Вывод
Температура на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое —0.203.
Время работы программы: 0.203
Вывод
Давление на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое -0.203.
Возникновение силы тяги от действия давления газа схематично показано на рисунке:
Время работы программы: 0.203
Вывод
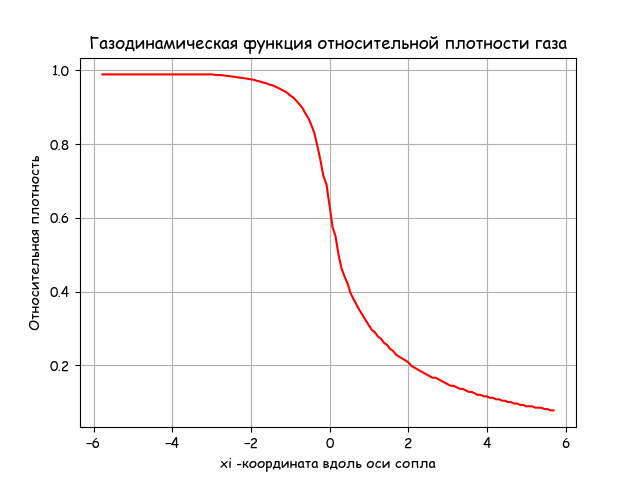
Плотность газа на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое.
Видео:Урок 106. Реактивное движениеСкачать

Тяговые и расходные характеристики сопла
ОБЩИЕ СВЕДЕНИЯ
Назначение выходных устройств.
Основные параметры режима и критерии
Эффективности работы
Назначение. Обязательным элементом выходных устройств является сопло на двигателях прямой реакции или диффузорное устройство – на турбовальных двигателях (тяга которых не используется).
Сопло выполняет две основные функции: служит для преобразования тепловой и потенциальной энергии газа в кинетическую энергию вытекающей струи, т.е. для увеличения динамического импульса газового потока на выходе из двигателя и, соответственно, для увеличения тяги; обеспечивает заданную пропускную способность (определенное противодавление) на выходе из двигателя, тем самым с помощью сопла согласовываются режимы работы турбины и компрессора (гл. 10). Диффузорное выходное устройство служит для уменьшения давления за турбиной, т.е. для повышения теплоперепада на турбине и, соответственно, увеличения мощности двигателя.
Сопла двигателей сверхзвуковых летательных аппаратов выполняются регулируемыми, что позволяет оптимально согласовать работу компрессора и турбины в различных условиях эксплуатации и повысить эффективность применения силовой установки (см. гл. 13). Современные выходные устройства могут обеспечивать отклонение выходной струи (и соответственно управление вектором тяги) вплоть до изменения направления ее движения на противоположное. Они могут включать удлинительные трубы, системы подачи воздуха на охлаждение конструкции и т.п.

Внешний поток характеризуется числом М полета (М п), а основной поток целесообразно характеризовать максимальной приведенной скоростью газа в канале сопла, т.е. скоростью в выходном сечении l с, которая однозначно определяется отношением статического и полного давления газа в этом сечении. Это отношение с точностью до потерь полного давления определяется величиной
p с = p *т / p с – (3.1)
отношением полного давления газа в сечении Т на входе в сопло к статическому давлению в сечении C на выходе из него (обозначение сечений см. рис. 1.2).
Величина p с называется степенью понижения давления газа в канале сопла или действительной степенью понижения давления.
Действительная степень понижения давления не всегда равна располагаемой степени понижения давления, которой называют отношение полного давления газа на входе в сопло к давлению окружающей среды:
p с.р= p *т / p н. (3.2)
Величина p с.р и ее соотношение с p с являются основными параметрами, характеризующими работу данного сопла. Если p с.р= p с, то p с= p н, т.е. реализуется режим полного расширения (расчетный). В любом другом случае, когда p с.р ¹ p с, давление на выходе из сопла не равно атмосферному p с ¹ p н, т.е. имеют место режимы недорасширения или перерасширения (как правило, нерасчетные режимы работы).
Критерии эффективности. Эффективность работы сопла оценивается в общем случае тремя основными коэффициентами: скорости j с, тяги`Pс и эффективной тяги`Pс. эф.
Коэффициентом скорости называют отношение осевой составляющей действительной скорости истечения к идеальной (изоэнтропической) скорости при одинаковых в обоих случаях степенях понижения давления и одинаковых полных температурах газового потока:
j с= c с / c с s . (3.3)
Им учитываются внутренние потери, обусловленные вязкостью газа (трение о стенки и вихреобразование) и отклонением потока от осевого направления, а также возможным возникновением местных скачков уплотнения в проточной части сверхзвуковых выходных устройств.
Внутренние потери выходного устройства оцениваются в некоторых случаях коэффициентом восстановления давления
который представляет собой отношение полных давлений на выходе из сопла и на входе в него. Величины s с и j с взаимозависимы. Далее будет получена функциональная связь между ними.
Коэффициентом тяги`P с называют отношение тяги сопла P с к его идеальной тяге P с s при одинаковом (действительном) в обоих случаях расходе газа через сопло:
`P с = P с / P с s . (3.4)
Идеальной тягой сопла Pс sусловно называют динамический импульс в его выходном сечении, соответствующий изоэнтропическому (j с = 1) полному (p с = p н) расширению потока при заданной располагаемой степени понижения давления:
P с s = G г c с s . (3.5)
Тягой сопла P с условно называют сумму действительного динамического импульса в выходном сечении сопла и статической составляющей тяги (см. гл. 6):
P с = G г c с + F с ( p с – p н) . (3.5а)
Если соотношение (3.4) умножить и разделить на величину динамического выходного импульса P с.полн = G г c с.полн, который реализуется в условиях полного расширения при данной p с.р, то получим
`P с = j с K н , K н = P с / P с.полн, (3.4а)
где K н – коэффициент недорасширения (или перерасширения) потока.
На режимах полного расширения коэффициент тяги сопла равен коэффициенту скорости`P с =j с, так как при p с = p н величина K н = 1, а отношение действительной тяги сопла к идеальной равно отношению соответствующих скоростей истечения, поскольку расход газа через сопло G г предполагается одинаковым при его истечении с потерями и без них. На всех режимах, когда p с ¹ p н, коэффициент K н p кр. В этом случае l с= l кр= 1, а p с> p н. Это нерасчетные режимы работы;
3) критические при p с.р = p кр (граничный между двумя предыдущими). В этом случае p с = p н и l с= 1.
Тяговые характеристики на режимах полного расширения. При l с £ 1 осуществляется полное расширение потока (K н= 1) и коэффициент тяги `P с равен коэффициенту скорости j с.
Коэффициент скорости сопел современных ТРДД и ТРД изменяется в пределах j с = 0,97 . 0,995 (при уменьшении p с.р он незначительно снижается), т.е. эффективность сужающихся сопел на режимах полного расширения достаточно высокая.
Потери тяги от недорасширения потока. На режимах недорасширения в выходном сечении сужающегося сопла устанавливается давление
Рис. 3.3.Схема профилированного сужающегося сопла
и форма струи за ним на режиме недорасширения (p кр 1 сторону (от оси сопла); в возникающем косом скачке уплотнения давление повышается и становится равным атмосферному или несколько превышает его. На большей части поверхности кормы образуется разрежение и, как следствие, возникает кормовое сопротивление. Величина кормового сопротивления, как и внешнего сопротивления входного устройства, определяется по формуле: X кор = c x кор p н М 2п F mid, (3.15) где c х кор – коэффициент кормового сопротивления, который определяется обычно по результатам продувки выходного устройства, когда величина X кор замеряется. Он зависит от геометрии конкретного выходного устройства, от чисел М п и Rе, а также от режима работы сопла (p с.р). Коэффициент эффективной тяги. Зависимость`P с.эф от числа М п (при одновременном изменении p с.р= f (М п) согласно рис. 3.1), полученная по результатам экспериментальных исследований изолированного сужающегося сопла [35], представлена на рис. 3.7. Из него следует, что при увеличении числа М п от 0 до 1 и далее до 2 коэффициент эффективной тяги сужающегося сопла снижается от 0,97 . 0,98 до 0,95 . 0,93 и далее до 0,88 . 0,84. При больших скоростях полета указанным потерям выходного импульса соответствуют примерно вдвое большие потери тяги (разд. 3.1.2). Поэтому при М п = 2 снижение эффективной тяги двигателя, обусловленное потерями на недорасширение потока и на преодоление кормового сопротивления, достигает 30 %. Рассмотренные закономерности изменения потерь тяги одинаковы как для конических, так и для профилированных (см. рис. 3.3.) сужающихся сопел. Что касается расходных характеристик, то они для указанных сопел существенно неодинаковы. Расходные характеристики сужающегося сопла. Коэффициент расхода профилированных сопел большой и средней размерности близок к единице (m с @ 0,97 . 0,998) и поэтому относительная пропускная способность m с q (l с.кр) этих сопел в зависимости от располагаемой степени понижения давления при p с.р p кр сохраняется постоянной. Расходные характеристики сужающегося сопла (рис. 3.8), выполненного в виде конического насадка (см. рис. 1.5, а), имеют свои особенности. Главная особенность такого сопла заключается в том, что поля статического давления и скорости потока в его выходном сечении существенно неравномерны (что является следствием радиальной составляющей скорости): статическое давление у кромки близко к атмосферному даже при сверхкритической степени понижения давления, а к оси сопла оно нарастает, оставаясь всегда выше атмосферного, соответственно скорость потока у оси минимальная и остается всегда дозвуковой, а у кромки максимальная. При p с.р> p кр она сверхзвуковая, поскольку около кромки реализуется течение Прандтля-Майера с поворотом потока, как при обтекании тупого угла. Средняя скорость в выходном сечении всегда меньше звуковой и уменьшается при увеличении угла наклона образующей q. Неравномерность полей статического давления и скорости приводит к трем основным особенностям расходных характеристик этого сопла. Во-первых, максимальный коэффициент расхода и, соответственно, максимальная пропускная способность этого сопла зависят от угла q наклона образующей (см. рис. 3.8), заметно снижаясь с его увеличением. Это объясняется снижением средней скорости у оси вследствие увеличения статического давления. Во-вторых, максимальные коэффициент расхода и пропускная способность данного сопла реализуются не при критической p кр, а при более высокой располагаемой p с.р, которую называют степенью понижения давления стабилизации потока p с.стаб (ее называют также второй критической). Величина p с.стаб также зависит от угла наклона q, увеличиваясь с его увеличением. В-третьих, при снижении p с.р (на режимах p с.р 5. 7. Поэтому на двигателях больших сверхзвуковых скоростей полета применяются более сложные выходные устройства. 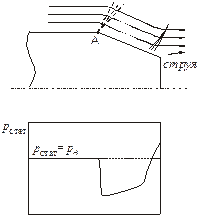



💥 Видео
Физика прямоточного двигателяСкачать

Сопротивление материалов. Лекция: косой изгиб и внецентренное растяжение-сжатиеСкачать

Спин детонационный двигатель. Детонационное сжатие топливаСкачать

Основное уравнение гидростатики (задачи)Скачать

Мотор на вращающейся платформеСкачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Классификация реакций: ионные и радикальные реакцииСкачать

Урок 96. Простейшие задачи на вращение твердого телаСкачать

определение реакций в стержнях от действия грузовСкачать

М1-5-2 Определение параметров деформируемости. Трехосное сжатие и полевые методыСкачать

Лекция III-5. Специальные методы лабораторных испытанийСкачать

Физика. 11 класс. Распространие механических волн. Интерференция механических волн /19.11.2020/Скачать

Измерение вязкостиСкачать

Волновой воздушно-реактивный двигательСкачать

Винтомоторная HONDA GX-670 24 л.с. Замер тяги и частоты вращения воздушного винта.Скачать

Техническая механика/Определение реакций в жесткой заделке.Скачать

Лабораторная работа «Измерение жёсткости пружины»Скачать