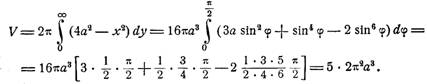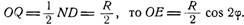Циссоида Диоклеса – плоская алгебраическая кривая 3-го порядка. Уравнение этой кривой в декартовой прямоугольной и в полярной системах координат имеет соответственно вид


Параметрические уравнения циссоиды Диоклеса имеют вид:
где 
В начале координат у кривой имеется точка возврата 1-го рода. Вертикальная асимптота имеет уравнение х = 2а. Площадь S между кривой и асимптотой:

Вместо производящей окружности, на которой лежат точки О и E, можно брать и другие кривые 2-го порядка.
Кривая названа по имени древнегреческого математика Диоклеса (Ш век до нашей эры), применявшего её в решении делосской задачи (т.е. задачи об удвоении куба). При этом древние греки рассматривали только часть циссоиды, лежащую внутри производящей окружности; эта часть циссоиды вместе с дугой окружности напоминают лист плюща. Этим и объясняется название кривой: оно произошло от греческого слова χισσειδήζ – плющевидный, похожий на лист плюща, которое, в свою очередь, пошло от χισσοζ – плющ и ειδος – вид, форма.
Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Циссоида Диоклеса
1. Особенности формы. Среди многих способов образования циссоиды—кривой, открытой древними в поисках решения знаменитой задачи об удвоении куба, мы остановимся сначала на простейшем. Возьмем окружность (называемую производящей) с диаметром ОА=2а и касательную АВ к ней. Через точку О проведем луч ОВ и на нем отложим отрезок ОМ=ВС. Построенная таким образом точка М принадлежит циссоиде. Повернув луч 0В на некоторый угол и проделав указанное построение, мы найдем вторую точку циссоиды, и т. д. (Рис. 3).
Если точку О принять за полюс, то 


Пользуясь формулами перехода от полярных координат к декартовым, найдем уравнение циссоиды в прямоугольной системе:
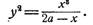
Параметрические уравнения циссоиды можно получить, полагая x=ty, тогда, на основании уравнения (2), придем к системе
Уравнение (2) показывает, что циссоида является алгебраической кривой 3-го порядка, а из уравнений (3) следует, что она является рациональной кривой.
Циссоида симметрична относительно оси абсцисс, имеет бесконечные ветви; касательная к производящей окружности, т. е. прямая х = 2а, служит для нее асимптотой; начало координат является точкой возврата 1-го рода.
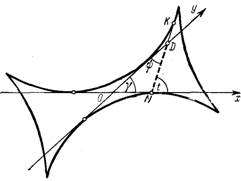
2. Свойства. Кинематически циссоида может быть получена как траектория середины М катета ВС треугольника АВС, передвигающегося в плоскости чертежа так, что его вершина В скользит по оси ординат, а другой катет АС всегда проходит через неподвижную точку Е на оси абсцисс. (Рис. 4)
Действительно, обозначив середину отрезка ОЕ через D , замечаем, что поскольку ВС=ЕО, ê ВСЕ= ê ВЕО, откуда /_ ВЕО = /_ СВЕ, и, следовательно, ê NBE — равнобедренный, а так как Е D =ЕО/2=ВС/2=ВМ, то отрезок DM параллелен отрезку BE . Пусть, далее, точка К есть точка пересечения с продолжением отрезка DM прямой, проходящей через точку В параллельно оси абсцисс. Опишем окружность с центром в начале координат и радиусом, равным OD, и проведем к ней касательную во второй точке пересечения с прямой ЕО. Она пройдет, очевидно, через точку К. Обозначив точку пересечения прямой DMK с окружностью через F , заметим, что треугольники DOF и МВК равны между собой. Из равенства их следует, что DF = MK , а значит, и DM = FK . Последнее равенство и показывает, что геометрическое место точек М будет циссоидой.
Другие способы образования циссоиды основаны на ее соотношениях с параболой. Покажем в первую очередь, что циссоида является подэрой параболы относительно ее вершины.
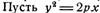

начала координат на эту касательную, будет 

Исключая из этих равенств параметр h, мы получим уравнение

Заметим далее, что координаты точки, симметричной началу координат относительно касательной к параболе у 2 = 2рх, получатся, если правые части формул (4) удвоить, и, следовательно, определятся формулами
Исключая из этих равенств параметр h, мы снова получим циссоиду с уравнением 
Следует заметить, что геометрическое место точек, симметричных началу координат относительно касательной к параболе, можно рассматривать как траекторию вершины другой параболы, одинаковой с данной, которая катится по данной параболе. Таким образом, возникает новый способ кинематического образования циссоиды как траектории вершины параболы, которая без скольжения катится по другой такой же параболе.
Остановимся на метрических свойствах циссоиды; при этом нам будет удобно пользоваться параметрическими уравнениями циссоиды в виде
Площадь, ограниченная циссоидой и ее асимптотой, равняется утроенной площади производящего круга; действительно,
Это соотношение получено было Гюйгенсом и независимо от него Ферма.
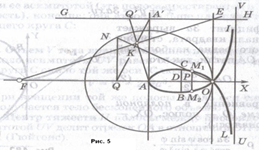
Определяя площадь криволинейного треугольника ОАМС (рис.5), найдем, интегрируя в границах 



Объем тела, образованного вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат определится по формуле
Если учесть, что объем тора, получаемого от вращения производящего круга вокруг оси ординат, равняется 
Пусть теперь хс — абсцисса центра тяжести части плоскости, ограниченной циссоидой и ее асимптотой; тогда по теореме Гюльдена будем иметь V == U • 2pхс, где V и U—соответственно объем и площадь, которые были определены выше. Подставляя их значения
в соотношение Гюльдена, получим
Таким образом, центр тяжести части плоскости, ограничиваемой циссоидой и ее асимптотой, делит отрезок между вершиной и асимптотой на две части, отношение которых равно 5.
Это соотношение позволяет в свою очередь определить объем тела, полученного вращением циссоиды вокруг ее асимптоты. По теореме Гюльдена будем иметь
Этот результат можно истолковать также как объем тора, полученного от вращения производящего круга вокруг асимптоты. Таким образом, объем тела, полученного вращением циссоиды вокруг ее асимптоты, равен объему тора, полученного от вращения производящего круга. Это соотношение установлено впервые Слюзом.
Длина дуги циссоиды от ее вершины до точки с абсциссой х определится по формуле
3.Применение циссоиды к решению делосской задачи. Как уже говорилось, циссоида была открыта древними в поисках решения делосской задачи об удвоении куба. История возникновения этой задачи, согласно легенде, передаваемой Эратосфеном, такова: на острове Делосе жители страдали от мора, посланного им богами; по предсказанию оракула богов можно было умиротворить, удвоив объем жертвенника, имевшего форму куба. Суть задачи сводилась к определению ребра куба, объем которого был бы в два раза больше объема данного куба. Что касается самого повода постановки задачи, то справедливо полагать, что «пифия находилась скорее под внушением математиков, нежели вдохновлялась самим богом» (Цейтен), так как задача об удвоении куба являлась естественным перенесением в пространство планиметрической задачи о построении квадрата с площадью, в два раза большей площади данного квадрата, и, следовательно, могла скорее возникнуть в сознании математика, нежели в сознании оракула.
Открытие циссоиды для целей решения делосской задачи приписывается Диоклесу, жившему в 3 веке до нашей эры. Возможность найти графическим путем ребро куба с объемом, в два раза большим объема данного куба, усматривается из следующих соображений. Пусть b – ребро данного куба, а В – ребро искомого; тогда 

Перепишем для этой цели уравнение циссоиды в виде 


и пересекает циссоиду в точке М, координаты которой удовлетворяют уравнению
Это уравнение можно рассматривать как уравнение прямой, проходящей через точку А (2а, 0) и отсекающей на оси ординат отрезок

Если теперь принять 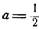
Древние рассматривали только ту часть циссоиды, которая находится внутри производящего круга. Вместе с дугой окружности производящего круга эта часть образует фигуру, напоминающую лист плюща, откуда проистекает название кривой. Наличие бесконечных ветвей у циссоиды было установлено в 17 веке Робервалем и независимо от него Слюзом. Кинематический способ образования циссоиды с помощью треугольника приписывается Ньютону, который выполнил также спрямление циссоиды не только аналитическим путем, но и графическим.
Кардиоида
1.Уравнение. Кардиоиду можно определить как траекторию точки, лежащей на окружности круга радиуса r, который катится по окружности неподвижного круга с таким же радиусом. Она будет представлять собой, таким образом, эпициклоиду с модулем m, равным 1.
Это обстоятельство позволяет сразу же записать параметрические уравнения кардиоиды, заменяя в ранее приведенных параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:

Чтобы получить полярное уравнение кардиоиды, удобно принять за полюс точку А (рис.7), а полярную ось направить по оси абсцисс. Так как четырехугольник AOO1M будет равнобедренной трапецией, то полярный угол j точки М окажется равным углу поворота производящего круга, т. е. параметру t. Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через r sin t. Сокращая полученное таким образом равенство на sin t, получим полярное уравнение кардиоиды
По виду этого уравнения
можно заключить, что кардиоида является одной из улиток Паскаля. Она может быть определена, следовательно, как конхоида круга.
Переводя уравнение (2) в прямоугольную систему координат, получим:

Из этого уравнения следует, что кардиоида является алгебраической кривой 4-го порядка.
2. Свойства. Прежде всего, поскольку кардиоида является эпициклоидой с m=1, на нее можно перенести все свойства рассмотренных нами в предыдущем параграфе эпициклоид.
Вот эти свойства и характеристики.
1. Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположную точке касания кругов, а нормаль — через точку их касания.
2. Угол m, составляемый касательной к кардиоиде с радиусом-вектором точки касания, равен половине угла, образуемого этим радиусом-вектором с полярной осью. Действительно
Из этого соотношения непосредственно вытекает, что угол, составляемый касательной к кардиоиде с осью абсцисс, равняется 
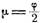
Действительно, так как
Заметим еще, что геометрическое место точек пересечения этих касательных есть окружность 


3. Радиус кривизны в произвольной точке кардиоиды определится по формуле

Можно показать также, что радиус кривизны равняется 2/3 полярной нормали N в заданной точке.
Действительно, 

4. Эволюта кардиоиды, согласно общему свойству эволют эпициклоид, будет также кардиоидой, подобной данной, с коэффициентом подобия, равным 1/3, и повернутой относительно данной на угол 180°.
5. Длина дуги кардиоиды от точки А до произвольной точки М определится по формуле

Если длину дуги отсчитывать от точки А1, диаметрально противоположной точке А, то формула для определения длины дуги может быть записана в виде

6. Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид

7. Площадь, ограниченная кардиоидой, определится по формуле
и, как видно, равна ушестеренной площади производящего круга.
Длина всей кардиоиды определится по формуле
и, как видно, равна восьми диаметрам производящего круга. Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен
Поверхность тела, полученного от вращения кардиоиды вокруг ее оси, равняется
Мы видели, что кардиоида органически связана с окружностью. Она является конхоидой круга и эпициклоидой. Она имеет с окружностью и иной характер родства — кардиоида является подэрой окружности относительно точки, принадлежащей этой окружности.
Действительно, пусть ОМ есть перпендикуляр, опущенный на касательную к окружности с радиусом, равным 2r, проведенную в точке N.
Так как ОМ = OB + ВМ, или r == 2r cos j + 2r, то геометрическим местом точек М будет кардиоида с уравнением r = 2r (1 + cos j).
Заметим в заключение, что кардиоида относится также к семейству синусоидальных спиралей, и отдельные свойства ее повторяют общие свойства этих кривых. Из этих свойств следует, в частности, что инверсия кардиоиды, относительно точки возврата дает параболу.
Астроида
1. Свойства. Астроида, как и рассмотренная выше кривая Штейнера, является частным случаем гипоциклоид, а именно, гипоциклоидой с модулем m, равным 1/4. Она представляет собой, следовательно, траекторию точки, лежащей на окружности круга радиуса r, который катится по внутренней стороне другого, неподвижного круга, радиус R которого в четыре раза больше.
Параметрические уравнения астроиды можно получить, полагая в уравнениях гипоциклоиды, m=1/4. Вот эти уравнения:
где t, как и ранее, угол поворота производящего круга (рис. 10)
Исключая из уравнений (1) параметр t, получим:

Из уравнения (2) следует, что астроида является алгебраической кривой 6-го порядка.
Параметрические уравнения (1) астроиды можно привести к виду

Исключая из этих уравнений параметр t, получим часто употребляемый вид уравнения астроиды

Полагая в ранее выведенных общих соотношениях для циклоидальных кривых модуль
m = -1/4, получим соответствующие соотношения для астроиды:
1) радиус кривизны в произвольной точке астроиды определяется по формуле

2) длина дуги астроиды от точки А до произвольной точки M(t) определится по формуле

длина одной ветви равна 
3) для получения натурального уравнения астроиды заметим предварительно, что если началом отсчета длины дуги полагать не точку А, для которой t = 0, а точку, для которой t = p, то длина дуги определится формулой
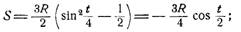
исключая параметр t из уравнений (5) и (6), получим натуральное уравнение астроиды
4) эволюта астроиды есть также астроида, подобная данной, с коэффициентом подобия, равным 2, повернутая относительно данной на угол p/4 (рис.11)
5) площадь, ограниченная всей астроидой, равна 
поверхность тела, образованного вращением астроиды, равна
Обратимся теперь к рассмотрению некоторых частных свойств астроиды.
Астроида является огибающей отрезка постоянной длины, концы. которого скользят по двум взаимно перпендикулярным прямым.
Принимаем эти прямые за оси координат и, обозначая угол наклона скользящего отрезка ND=R через a (рис.12), будем иметь уравнение прямой ND в виде
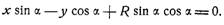
Дифференцируя это уравнение по параметру a, получим:
Исключая из последнего уравнения и уравнения (7) параметр a, будем иметь уравнение огибающей в виде 
Практически перемещение отрезка ND можно осуществить с помощью так называемых кардановых кругов. Один из этих кругов с радиусом R неподвижен, а другой, с радиусом r, в два раза меньшим, катится по внутренней стороне неподвижного круга. Любые две диаметрально противоположные точки N и D катящегося круга будут перемещаться по двум взаимно перпендикулярным диаметрам Ох и Оу неподвижного круга. Ясно, что огибающей диаметра катящегося круга и будет астроида.
 Рис. 11 Рис. 11 |  Рис. 12 Рис. 12 |
Рассмотренный способ образования астроиды можно истолковать также следующим образом. Прямоугольник ODCN, две стороны которого лежат на двух взаимно перпендикулярных прямых, деформируется так, что диагональ его сохраняет длину, равную R, огибающая диагонали и будет астроидой. Так как при этом перпендикуляр, опущенный из вершины С на диагональ DN, служит нормалью к огибающей, то астроида представляет собой геометрическое место оснований перпендикуляров, опущенных из вершины С прямоугольника на его диагональ.
2. Свойства касательных к астроиде. Уравнение (7) выражает прямую ND, т. е. касательную к астроиде в некоторой точке М, причем параметр a представляет собой угол, составляемый этой касательной с осью абсцисс. Уравнение другой касательной, перпендикулярной к первой, будет иметь вид

Исключая из уравнений (7) и (8) параметр а, получим уравнение 

Другое свойство касательных к астроиде таково: каждая касательная пересекает астроиду в двух точках, касательные в которых пересекаются в точке, лежащей на окружности описанного около астроиды круга.
Определим подэру астроиды относительно точки Р, лежащей на биссектрисе 1-го координатного угла на расстоянии ОР=с от начала координат. Выше было показано, что астроиду можно рассматривать как огибающую отрезка ND = R, скользящего своими концами по координатным осям. Отсюда
следует, что искомую подэру можно определить как геометрическое место оснований перпендикуляров, опущенных из точки Р на прямую ND (рис. 13). Проведем ОЕ _|_ ND, и OQ, где Q — середина отрезка ND. Точку Р посчитаем полюсом, а прямую РК полярной осью. Полярный угол КРМ точки М подэры обозначим через j, а радиус-вектор РМ — через r. Тогда, как легко видеть, угол
Так как
Но, с другой стороны, 

Полученная таким образом кривая 6-го порядка имеет в начале координат четырехкратную точку и называется «жуком». В частном случае, пои с=0, жук становится розой,
3. Косая астроида. Обобщением рассмотренной астроиды является так называемая косая астроида, которая представляет собой огибающую отрезка ND постоянной длины R, скользящего своими концами по двум прямым, пересекающимся под произвольным углом f.
Полагая эти пересекающиеся прямые координатными осями, обозначим угол, составляемый прямой ND с осью абсцисс, через t. Тогда из треугольника OND (рис. 14) будем иметь:
и следовательно, уравнение прямой ND в отрезках на осях запишется в виде
Дифференцируя это уравнение по t и исключая из полученного после дифференцирования равенства и уравнения прямой параметр t, получим параметрические уравнения косой астроиды в виде
при 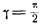
Видео:Физика Изучение графиков изопроцессовСкачать

Циссоида Диокла
2. Циссоида Диокла
2.1 Определение и построение
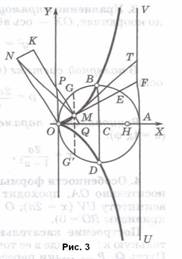
На отрезке OA = 2a, как на диаметре, строим окружность C (рис.3) и проводим через A касательную UV. Через O проводим произвольную прямую OF, пересекающую UV в точке F; эта прямая пересечет (вторично) окружность C в точке E. На прямой OF от точки F по направлению к O откладываем отрезок FM, равный хорде OE.
Линия, описываемая точкой M при вращении OF около O, называется циссоидой Диокла – по имени греческого ученого 2 века до н.э., который ввел эту линию для графического решения задачи об удвоении куба.
Особенности формы. Циссоида симметрична относительно OA, проходит через точки B, D и имеет асимптоту UV (x = 2a); O – точка возврата (радиус кривизны RO = O).
Построение касательной. Чтобы построить касательную к циссоиде в ее точке M, проводим MP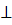
2.2 Исторические сведения
Диокл определял циссоиду с помощью другого построения. Он проводил диаметр BD, перпендикулярный OA; точка M получалась в пересечении хорды OE с прямой GG ̕ 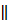
Примерно в 1640 г. Роберваль, а позднее Р. де Слюз заметили, что циссоида неограниченно продолжается и за пределы окружности, если точка E описывает и другую полуокружность BOD; тогда M лежит на продолжении хорды OE. Однако наименование «циссоида Слюза», предложенное Гюйгенсом, не утвердилось в литературе.
2.3 Площадь S полосы
заключенной между циссоидой и ее асимптотой (эта полоса простирается в бесконечность), конечна; она втрое больше площади производящего круга C:
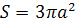
2.4 Объем V тела вращения
вышеупомянутой полосы около асимптоты UV равен объему V̕ тела вращения круга C около той же оси (Слюз):
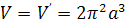
При вращении той же полосы около оси симметрии получается тело бесконечного объема.
Дана циссоида Диокла с полюсом в точке O, осью OA и параметром 2a. Приняв точку O за полюс, а ось кривой за ось полярной системы, вывести уравнение кривой в полярных координатах. Записать уравнение кривой в прямоугольной декартовой системе координат.
Пусть O – начало координат, OX – ось абсцисс. Тогда уравнение в прямоугольной системе координат:
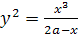
Если O – полюс и OX – полярная ось, то уравнение в полярных координаты будет иметь вид:
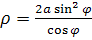
3. Декартов лист
3.1 Исторические сведения
В 1638 г. Р. Декарт, чтобы опровергнуть (неверно им понятое) правило П. Ферма для нахождения касательных, предложил Ферма найти касательную к линии 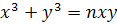
Но в таком виде ее представил впервые Х. Гюйгенс (в 1692 г.). До этого линию 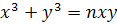
Чтобы построить декартов лист с диаметром петли 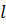
Через O проводим любую прямую ON и через точку N, где эта прямая пересекает (вторично) окружность, проводим NQ
Когда точка N, исходя из O, описывает окружность A против часовой стрелки, точка M1 описывает траекторию LOCABOI.
💡 Видео
Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

По графику, приведённому на рисунке 6.15, найдите амплитуду ЭДС индукции, период и частоту обращенияСкачать

Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать

Гальванические элементы. 1 часть. 10 класс.Скачать

Предельные вероятности состоянийСкачать

2. ВидыСкачать
Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Основы инженерной графики. Лекция 1. Точка и прямая в пространствеСкачать

Сопряжение окружностейСкачать

Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Гидрируем и дегидрируем углеводородыСкачать

Инженерная графика. Виды разрезы сеченияСкачать

Двоичная система счисления — самое простое объяснениеСкачать

Задание 34 Варианты 4 (5, 6) Группа геометрических телСкачать

ТРИ ВИДА ПРОЕКЦИИ ДЕТАЛИ И ПОЛЕЗНЫЕ РАЗРЕЗЫ. Черчение и инженерная графика.Скачать

НАЧЕРТИТЬ ЗАСОВ. ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ. ИНЖЕНЕРНАЯ ГРАФИКА. ПЕРЕХОДЫ И СОПРЯЖЕНИЯСкачать