Центр колеса катящегося по прямолинейному участку пути движется согласно уравнениям (5 видео)

Содержание

Центр колеса катящегося по прямолинейному участку пути движется согласно уравнениям
Теоретическая механика (стр. 31 )
Задача 1.1 (3)
🌟 Видео

Видео:Мгновенный центр вращенияСкачать

Центр колеса катящегося по прямолинейному участку пути движется согласно уравнениям

Глава 9. Плоскопараллельное движение твердого тела.

9.1. Уравнение движения плоской фигуры.

9.1.1. Зависят ли при плоскопараллельном движении значение и направление угла повopoтa твердого тела от выбора полюса? (Ответ Нет)

9.1.2. Зависит ли при плоскопараллельном движении твердого тела вид уравнений движения полюса от его выбора? (Ответ Да)

9.1.3. Стержень АВ движется согласно уравнениям х_А = 2 + t 2 , у_А = 0, φ = 0,25 πt. Определить абсциссу точки В в момент времени t₁ = 1 с, длина АВ = 3м. (Ответ 0,879)

9.1.4. Центр колеса, катящегося по прямолинейному участку пути, движется согласно уравнениям х_с = 0,3t 2 , y_c = 0,15 м. Определить в момент времени t₁ = 1 с ординату точки В, если в начале движения прямая АВ совпадала с осью О_у. (Ответ 0,212)

9.1.5. Балка AD движется согласно уравнениям х_А = t 2 , у_А = 0, φ = arcsin [2/ [4 + (3,5 — t 2 ) 2 ] 0,5 ]. Определить абсциссу точки А в положении балки, когда ее угол поворота φ = 38°. (Ответ 0,940)

9.1.6. Вследствие удара колесо радиуса R = 0,2 м катится с постоянной скоростью центра v_c = 0,1 м/с. Определить абсциссу точки A в момент времени t₁ = 1 с, если в момент t₀ = 0 точка A находилась в начале координат. (Ответ 4,11•10 -3 )

9.1.7. Вершины А и В треугольника во время движения все время находятся соответственно на осях О_у и О_х. Определить угол поворота φ в момент времени t₁ = 2 с, если вершина В из положения Х_В(0) = 2 м начала перемешаться с постоянной скоростью v_B =0,5 м/с; длина АВ = 4 м. (Ответ 0,846)

9.1.8. Колесо радиуса R = 10 см катится по прямолинейному участку пути с постоянным ускорением центра колеса а_с = 2π, где а_с — в см/с. Определить, сколько оборотов совершило колесо в момент времени t₁ = 10 с, если скорость v_с(0) = 0. (Ответ 500)

9.1.9. Кривошип ОА начал равномерно вращаться из состояния покоя с угловым ускорением ε_оа = 0,1π. Определить, сколько оборотов совершит шестерня 2 по истечении 10 с. Радиусы шестерен r₁ = r₂ = 10 см. (Ответ 5)

Видео:Центростремительное ускорение. 9 класс.Скачать

Теоретическая механика (стр. 31 )

Центр колеса катящегося по прямолинейному участку пути движется согласно уравнениям

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

3. Угловая скорость тела изменяется согласно закону (-8t). Определить угол поворота тела в момент времени t=3 c, если при to=0, угол поворота начальный равен 5 рад.

4. Ротор электродвигателя, начав вращаться равномерно, сделал за первые 5 с 100 оборотов. Определите начальное угловое ускорение ротора.

5. Частота вращения маховика за время t1=10 c уменьшилась в 3 раза и стала равной 30 об/мин. Определить угловое ускорение вала, если он вращается равномерно.

6. Угловая скорость тела изменяется согласно закону w=2t. Определите угловую скорость тела в момент времени t=4 c, если при to=0, угловая скорость равна нулю.

7. Скорость точки на расстоянии r=0,2 м от оси вращения изменяется по закону V=4t2. Определить угловое ускорение данного тела в момент времени t=2 c.

8. Маховик вращается с постоянной частотой вращения равной
90 об/мин. Определить ускорение точки маховика на расстоянии 0,043 м от оси вращения.

9. Нормальное ускорение точки М диска, вращающегося вокруг неподвижной оси равно 6,4 м/с2. Определить угловую скорость этого диска, если его радиус равен R=0,4 м.

10. Угловая скорость тела изменяется по закону w=t2. Определить ускорение точки этого тела на расстоянии r=0,2 м от оси вращения в момент времени t=1с.

Плоскопараллельное движение твёрдого тела

1. Зависит ли при плоскопараллельном движении значение и направление угла поворота твёрдого тела от выбора полюса?

2. Зависит ли при плоскопараллельном движении твёрдого тела вид уравнений движения полюса от его выбора?

3. Колесо радиуса R=10 см катится по прямолинейному участку пути с постоянным ускорением центра колеса ас=2П см/с2. Определите, сколько оборотов совершило колесо в момент времени t1=10 с, если начальная скорость центра колеса Vco=0.

4. Твёрдое тело совершает плоскопараллельное движение согласно уравнениям Ха=2t2, Ya=0,2, j=10t. Определите угловую скорость тела в момент времени t1=1 c.

5. Твёрдое тело касается плоскости, проходящей через ось Ох, в точке А и в данный момент времени совершает мгновенное вращение относительно этой точки. Определить угловую скорость тела, если скорость точки С равна 10 м/с, а расстояние АС=20 см.

6. Определить угловую скорость колеса, катящегося по неподвижной плоскости, если его радиус равен 0,2 м, точка А, отстоящая от центра колеса на 0,5r по вертикальному диаметру, имеет скорость Va=10 м/с.

7. Стержень АВ длиной 60 см движется параллельно оси Ох. В некоторый момент времени точки А и В стержня имеют скорости

VА=VВ=0,5 м/с и VА параллелен VВ и направлены вертикально вверх. Определите модуль мгновенной угловой скорости стержня.

8. Стержень АВ длиной 80 см параллелен оси Ох. В некоторый момент времени, точки А и В стержня имеют скорости VА=VВ=0,5 м/с и VА параллелен VВ и напралены вертикально вниз. Определите угловую скорость стержня.

9. Зависит ли при плоскопараллельном движении угловое ускорение твёрдого тела от выбора полюса?

10. Колесо катится по оси Ох согласно уравнениям Хс=2t2, Yc=0,5 м. Определить угловое ускорение колеса.

Сложное движение точки

1. Платформа движется по горизонтали со скоростью 1 м/с. относительно платформы в том же направлении движется точка по закону S=0,5t. Найти координату х точки в момент времени t=4 c, если при t=0, x=0.

2. Тележка катится прямолинейно по закону S=2t. Относительное движение точки М по тележке задано уравнениями Хм=3t и Yм=4t. Определите абсолютную скорость точки М в момент времени t=1 c.

3. Тележка движется по горизонтальной оси. В данный момент времени переносное ускорение тележки равно 2. По тележке движется точка М согласно уравнениям х=0,3t2, y=0,5t2. Определить абсолютное ускорение точки М.

4. Точка М движется от начала координат со скоростью V=2 м/с по стержню, образующему угол в 30 градусов с вертикальной осью вращения Oz. Угловая скорость равна 4 рад/с. Определить проекцию на ось Ох кориолисова ускорения точки М, когда стержень находится в плоскости Oyz.

5. По ободу полукруга, вращающегося вокруг горизонтального диаметра с угловой скоростью 4 рад/с, движется точка М с относительной скоростью Vотн =2 м/с. Для крайнего верхнего положения точки определить ускорение Кориолиса.

6. По горизонтальному диаметру диска, вращающегося вокруг вертикальной оси, проходящей через крайнюю правую точку диска, с угловой скоростью равной 2t, движется точка М с относительной скоростью Vотн=4t. Определите модуль ускорения кориолиса точки М в момент времени t=2 c.

7. Точка М движется с постоянной скоростью V=1 м/с от начала координат по стержню, вращающемуся в плоскости Oxy с постоянной угловой скоростью равной 2 рад/с. Определить модуль ускорения точки М, когда расстояние ОМ=0,5 м.

8. Корабль движется прямолинейно со скоростью Vo=10 м/с. На высоте h=1000 м над морем со скоростью V=20 м/с летит самолёт тем же курсом. Определить расстояние, отсчитываемое по горизонтали, на котором надо сбросить вымпел, чтобы он попал в корабль.

9. Кольцо радиуса r=0,5 м вращается с постоянной угловой скоростью 4 рад/с против часовой стрелки в плоскости Oxy относительно крайней левой точки горизонтального диаметра. По кольцу перемещается точка М с постоянной скоростью V=2 м/с. Определить модуль абсолютного ускорения точки М в крайнем правом положении на горизонтальном диметре.

10. Горизонтальная трубка вращается вокруг перпендикулярной оси с угловой скоростью 1,5 рад/с. Шарик движется вдоль трубки по закону МоМ=4t. Найти модуль ускорения Кориолиса шарика.

Сложное движение твёрдого тела

1. Скорость вертолёта равна 12 м/с, а угловая скорость несущего винта 15 рад/с. Определить координату х точки пересечения мгновенной оси вращения винта с плоскостью Oxy.

2. Квадратная пластина со стороной а=0,5 м участвует одновременно в поступательном движении со скоростью V=3 м/с вдоль оси х и в двух взаимно противоположных вращениях в своей плоскости с угловыми скоростями равными 4 рад/с. Определить модуль абсолютной поступательной скорости пластины.

3. Тело имеет скорость поступательного движения V=7 м/с и угловую скорость. Определить модуль скорости поступательного движения кинематического винта, если угол между векторами скорости и угловой скорости равен 70 градусов.

4. Векторы скорости полюса Vo и угловой скорости тела образуют угол в 30 градусов. Определить, на каком расстоянии от оси мгновенного вращения находится ось кинематического винта, если Vo=6 м/с, угловая скорость равна 6 с-1.

5. Тело одновременно находится в двух вращательных движениях вокруг параллельных осей с угловыми скоростями 2 рад/с и 3 рад/с, векторы которых направлены в одну сторону. Определить модуль абсолютной угловой скорости движения тела.

6. Вращение кривошипа ОА плоского механизма определяется уравнением (cos2t). В точке А к кривошипу присоединено колесо, которое вращается относительно кривошипа с угловой скоростью 3 рад/с, определить модуль абсолютной угловой скорости колеса в момент времени t=2 с.

7. Тело одновременно участвует в двух вращательных движениях с угловыми скоростями (2i+5j) и (4i+3j) соответственно. Определить модуль абсолютной угловой скорости тела.

8. Диск радиуса r=0,5 м участвует одновременно в двух вращательных движениях, с угловыми скоростями равными 2 рад/с, направленными от центра диска по оси Ох и по оси Оу. Определить модуль скорости точки диска, для которой этот модуль имеет максимальное значение.

9. Тело одновременно участвует в двух поступательных движениях со скоростями V1=5i+2j и V2=-2i+3j. Определить модуль абсолютной скорости тела.

10. Тело одновременно участвует в трёх поступательных движениях со скоростями V1=4i-3j+k, V2=-6i+5j+3k, V3=2i+2j-k. Определить модуль абсолютной скорости тела.

Основные теоремы динамики

1. Каков должен быть коэффициент трения колес заторможенного автомобиля о дорогу, если при скорости езды 20 м/с он останавливается через 6 секунд после начала торможения?

2. По шероховатой наклонной плоскости, составляющей угол 30о с горизонтом, спускается тяжелое тело без начальной скорости. Определить в течение какого времени тело пройдет путь длиной 39.2 метра, если коэффициент трения равен 0.2?

3. Вычислить работу, которая производится при подъеме груза массой 20 кг по наклонной плоскости на расстояние 6 метров, если угол плоскости с горизонтом 30о, а коэффициент трения равен 0,01?

Видео:9.1. Уравнения движения плоской фигурыСкачать

Задача 1.1 (3)

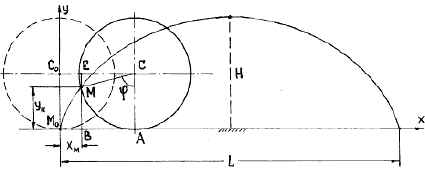
Найти уравнения движения точки М обода колеса радиуса R вагона, который движется по прямолинейному участку пути со скоростью V. Колесо катится без скольжения. Точка М в начальный момент движения соприкасалась с рельсом, т.е. занимала положение М₀ (рис. 1.1).

Изобразим на расчетной схеме (рис. 1.1) оси координат х и у, начало координат поместим в начальное положение точки М₀.

Рассмотрим два положения колеса: в начальный момент t = 0 и в текущий момент времени t.

Отметим положение точки М на ободе колеса и положение центра С колеса в момент t, координаты точки: x_м = М₀В, у_м = МВ.

Расстояние от центра колеса до рельса остается постоянным и равным R; это значит, что центр C колеса движется по прямой, параллельной оси х. За время t центр колеса переместится на расстояние C₀C = Vt (закон равномерного движения точки C), одновременно колесо повернется на угол j .

Чтобы получить уравнения движения точки М, надо координаты этой точки представить как функции времени.

Из расчетной схемы (рис. 1.1) видно, что

Из треугольника МЕС имеем;

МЕ = Rsin (90° – j ) = Rcosj ,

ЕC = Rcos (90° – j ) = Rsinj ,

Тогда х_м = Vt – Rsinj , (a)

Найдем зависимость угла j от времени t: так как колесо катится без скольжения, то длина дуги АМ окружности обода колеса (рис.1.1) равна длине отрезка М₀А.

но длина дуги АМ равна также произведению радиуса R на центральный угол j ; поэтому Vt = Rj , отсюда .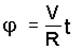

Теперь уравнения (а) будут иметь вид

; .

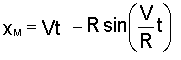
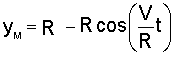
Полученные уравнения представляют собой уравнения движения точки М. В аналитической геометрии показано, что это параметрические уравнения циклоиды (параметром в данном случае является время t). Таким образом, траектория точки обода колеса, движущегося по прямолинейному участку пути без проскальзывания, является циклоидой. Длина одной ветви циклоиды L (рис. 1.1) равна 2p R, высота – H = 2R.