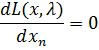Решение. Найдем экстремум функции F(X)=9·x1+x1 2 +6·x2+x2 2 , используя сервис функция Лагранжа :
L( X , λ )=F( X )+∑λi·φi( X )
где F( X ) — целевая функция вектора X , φi( X ) — ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция:
F(X) = 9·x1+x1 2 +6·x2+x2 2
Перепишем ограничение задачи в неявном виде: φi( X )= x1+x2-150=0
Составим вспомогательную функцию Лагранжа: L( X , λ ) = 9·x1+x1 2 +6·x2+x2 2 + λ(x1+x2-150)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·x1+λ+9 = 0
∂L/∂x2 = λ+2·x2+6 = 0
∂F/∂λ = x1+x2 -150= 0
Систему решаем с помощью метода Гаусса или используя формулы Крамера.
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Из 1-ой строки выражаем x3
Из 2-ой строки выражаем x2
Из 3-ой строки выражаем x1
Таким образом, чтобы общие издержки производства были минимальны, необходимо производить x1 = 74.25; x2 = 75.75.
Задание . По плану производства продукции предприятию необходимо изготовить 50 изделий. Эти изделия могут быть изготовлены 2-мя технологическими способами. При производстве x1 — изделий 1-ым способом затраты равны 3x1+x1 2 (т. руб.), а при изготовлении x2 — изделий 2-ым способом они составят 5x2+x2 2 (т. руб.). Определить сколько изделий каждым из способов необходимо изготовить, чтобы общие затраты на производство были минимальные.
Решение: составляем целевую функцию и ограничения:
F(X) = 3x1+x1 2 + 5x2+x2 2 → min
x1+x2 = 50
Пример №2 . В качестве целевой функции, подлежащей оптимизации, выступает функция: F(X) = x1·x2
при условии: 3x1 + x2 = 6.
Перепишем ограничение задачи в неявном виде: φi( X )=3x1 + x2 — 6 = 0
Составим вспомогательную функцию Лагранжа: L( X , λ )=x1·x2+λ(3x1 + x2 — 6)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 3·λ+x2 = 0
∂L/∂x2 = x1+λ = 0
∂F/∂λ = 3·x1 + x2-6 = 0
Решаем данную систему методом Гаусса.
Запишем систему в виде:
Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
Из 1-ой строки выражаем x3
Из 2-ой строки выражаем x2
Из 3-ой строки выражаем x1
Точка экстремума (1;3). Значение функции в точке экстремума F(1;3)=3.
Пример №3 . Рассмотрим функцию: F(X)=3·x1 2 +2·x2 2 -3·x1+1
и условия-ограничения: x1 2 + x2 2 = 4
L( X , λ )=3·x1 2 +2·x2 2 -3·x1+1 + λ(x1 2 + x2 2 — 4)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·x1·(λ+3)-3 = 0
∂L/∂x2 = 2·(λ+2)·x2 = 0
∂F/∂λ = x1 2 +x2 2 -4 = 0
Выражаем из первого уравнения x1:
Из второго уравнения получаем x2 = 0.
Подставляем в третье уравнение:

Перепишем в виде: λ+3 =3/4 откуда λ=-9/4.
Подставляя λ в выражение для x1, получаем:
Стационарная точка (2;0). Значение функции в стационарной точке: F(2;0) = 7.
Пример №4 . Найдем локальные стационарные точки функции:
F(X) = 3·x1·x2
g(x): 2·x1+x2=3
Перепишем ограничение задачи в неявном виде: 2·x1+x2-3 = 0
Составим вспомогательную функцию Лагранжа:
L = 3·x1·x2 + λ·(2·x1+x2-3)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·λ+3·x2 = 0
∂L/∂x2 = 3·x1+λ = 0
∂F/∂λ = 2·x1+x2-3 = 0
Данную систему решаем методом обратной матрицы:
Запишем матрицу в виде:
Вектор B: B T = (0,0,3)
Главный определить: ∆ = 0·(0·0-1·1)-3·(3·0-1·2)+2·(3·1-0·2) = 12
Транспонированная матрица:
Алгебраические дополнения 








Обратная матрица:
Вектор результатов X: X = A -1 ·B
x1 = 9 / 12 = 0.75
x2 = 18 / 12 = 1.5
λ = -27 / 12 = -2.25
Таким образом, локальный экстремум (0.75; 1.5). Значение функции в стационарной точке F(0.75; 1.5) = 3.375.
Пример №5 . Найдем точку экстремума функции:
F(X) = 2x1 2 +x1x2+x2 2 +2x1-4x2
Перепишем ограничение задачи в неявном виде:
φ1 = x1+x2-2 = 0
Составим вспомогательную функцию Лагранжа:
L = 2x1 2 +x1x2+x2 2 +2x1-4x2 + λ(x1+x2-2)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 4x1+λ+x2+2 = 0
∂L/∂x2 = x1+λ+2x2-4 = 0
∂F/∂λ = x1+x2-2 = 0
Решаем данную систему с помощью формул Крамера.
Запишем систему в виде:
B T = (-2,4,2)
Главный определитель:
∆ = 4 · (2 · 0-1 · 1)-1 · (1 · 0-1 · 1)+1 · (1 · 1-2 · 1) = -4 = -4
Заменим 1-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆1 = -2 · (2 · 0-1 · 1)-4 · (1 · 0-1 · 1)+2 · (1 · 1-2 · 1) = 4
Заменим 2-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆2 = 4 · (4 · 0-2 · 1)-1 · (-2 · 0-2 · 1)+1 · (-2 · 1-4 · 1) = -12
Заменим 3-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆3 = 4 · (2 · 2-1 · 4)-1 · (1 · 2-1 · (-2))+1 · (1 · 4-2 · (-2)) = 4
Стационарная точка: F(-1; 3).
Пример №6 . Найдем экстремум функции F(X) = x1·x2, используя функцию Лагранжа: L( X , λ )=F( X )+∑λi·φi( X ).
Примечание: решение ведем с помощью сервиса Функция Лагранжа онлайн
Видео:Лекция 9. Целевые функцииСкачать

Условный экстремум. Метод множителей Лагранжа. Первая часть.
Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.
Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.
Видео:Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать

Метод множителей Лагранжа для функций двух переменных.
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_^dx^2+2F_^dxdy+F_^dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F 0$, то $d^2F 0$, т.е. имеем условный минимум функции $z=f(x,y)$.
Примечание относительно формы записи определителя $H$. показатьскрыть
Некоторые авторы записывают определитель $H$ в иной форме (с знаком «-«):
В этой ситуации сформулированное выше правило изменится следующим образом: если $H > 0$, то функция имеет условный минимум, а при $H m$):
Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:
Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F 0.$$
Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_=z(1;3)=10$.
Аналогично, в точке $M_2(-1;-3)$ найдем:
$$H=8cdotleft| begin 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end right|= 8cdotleft| begin 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end right|=-40$$
Так как $H 0$. Следовательно, знак $H$ противоположен знаку $lambda$. Можно и довести вычисления до конца:
Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:
Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac$ получим $d^2F 0$, посему в данной точке функция имеет условный максимум, $z_=frac$.
Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:
Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.
Так как $ d^2F Bigr|_=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_=-10 dx^2 0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_=u(0)=0$. Так как $u_^(M_2) 0; ; y > 0. end right. $$
Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac$ и подставим найденное значение в первое уравнение: $5y-fraccdot frac=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac+frac-1=0$, $y^2=1$, $y=1$.
Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.
В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:
Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:
Подставляя $x=2$, $y=1$, $lambda=-10$, получим:
Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_=6$.
В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Алгоритм метода множителей Лагранжа
Метод множителей Лагранжа.
Метод множителей Лагранжа является одним из методов, которые позволяют решать задачи нелинейного программирования.
Нелинейное программирование-это раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и областью допустимых решений, определенной нелинейными ограничениями. В экономике это соответствует тому, что результаты (эффективность) возрастают или убывают непропорционально изменению масштабов использования ресурсов (или, что то же самое, масштабов производства): напр., из-за деления издержек производства на предприятиях на переменные и условно-постоянные; из-за насыщения спроса на товары, когда каждую следующую единицу продать труднее, чем предыдущую и т. д.
Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции
при выполнении условий
где x —вектор искомых переменных;
g (x) — функция ограничений (непрерывно дифференцируемая);
b — вектор констант ограничений.
Решение задачи нелинейного программирования (глобальный максимум или минимум) может принадлежать либо границе, либо внутренней части допустимого множества.
В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями. Иначе говоря, задача состоит в выборе таких неотрицательных значений переменных, подчиненных системе ограничений в форме неравенств, при которых достигается максимум (или минимум) данной функции. При этом не оговариваются формы ни целевой функции, ни неравенств. Могут быть разные случаи: целевая функция нелинейная, а ограничения линейны; целевая функция линейна, а ограничения (хотя бы одно из них) нелинейные; и целевая функция, и ограничения нелинейные.
Задача нелинейного программирования встречается в естественных науках, технике, экономике, математике, в сфере деловых отношений и в науке управления государством.
Нелинейное программирование, например, связано с основной экономической задачей. Так в задаче о распределении ограниченных ресурсов максимизируют либо эффективность, либо, если изучается потребитель, потребление при наличии ограничений, которые выражают условия недостатка ресурсов. В такой общей постановке математическая формулировка задачи может оказаться невозможной, но в конкретных применениях количественный вид всех функций может быть определен непосредственно. Например, промышленное предприятие производит изделия из пластмассы. Эффективность производства здесь оценивается прибылью, а ограничения интерпретируются как наличная рабочая сила, производственные площади, производительность оборудования и т.д.
Метод «затраты — эффективность» также укладывается в схему нелинейного программирования. Данный метод был разработан для использования при принятии решений в управлении государством. Общей функцией эффективности является благосостояние. Здесь возникают две задачи нелинейного программирования: первая — максимизация эффекта при ограниченных затратах, вторая — минимизация затрат при условии, чтобы эффект был выше некоторого минимального уровня. Обычно эта задача хорошо моделируется с помощью нелинейного программирования.
Результаты решения задачи нелинейного программирования являются подспорьем при принятии государственных решений. Полученное решение является, естественно, рекомендуемым, поэтому необходимо исследовать предположения и точность постановки задачи нелинейного программирования, прежде чем принять окончательное решение.
Нелинейные задачи сложны, часто их упрощают тем, что приводят к линейным. Для этого условно принимают, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению независимых переменных. Такой подход называется методом кусочно-линейных приближений, он применим, однако, лишь к некоторым видам нелинейных задач.
Нелинейные задачи в определенных условиях решаются с помощью функции Лагранжа: найдя ее седловую точку, тем самым находят и решение задачи. Среди вычислительных алгоритмов Н. п. большое место занимают градиентные методы. Универсального же метода для нелинейных задач нет и, по-видимому, может не быть, поскольку они чрезвычайно разнообразны. Особенно трудно решаются многоэкстремальные задачи.
Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителей Лагранжа.
С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде равенств. При этом задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Лагранжа.
Метод множителей Лагранжа заключается в сведении задач на условный экстремум к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.
Для задачи об экстремуме функции f (х1, x2. xn) при условиях (уравнениях связи) φi(x1, x2, . xn) = 0, i = 1, 2. m, функция Лагранжа имеет вид
Множители λ1, λ2, . λm наз. множителями Лагранжа.
Если величины x1, x2, . xn, λ1, λ2, . λm суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений


то при достаточно общих предположениях x1, x2, . xn доставляют экстремум функции f.
Рассмотрим задачу минимизации функции n переменных с учетом одного ограничения в виде равенства:
В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации:
минимизировать L(x,λ)=f(x)-λ*h(x) (3)
где Функция L(х;λ) называется функцией Лагранжа,
λ — неизвестная постоянная, которая носит название множителя Лагранжа. На знак λ никаких требований не накладывается.
Пусть при заданном значении λ=λ0 безусловный минимум функции L(x,λ) по х достигается в точке x=x0 и x0 удовлетворяет уравнению h1(x0)=0. Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (2), поскольку для всех значений х, удовлетворяющих (2), h1(x)=0 и L(x,λ)=min f(x).
Разумеется, необходимо подобрать значение λ=λ0 таким образом, чтобы координата точки безусловного минимума х0 удовлетворяла равенству (2). Это можно сделать, если, рассматривая λ как переменную, найти безусловный минимум функции (3) в виде функции λ, а затем выбрать значение λ, при котором выполняется равенство (2). Проиллюстрируем это на конкретном примере.
Соответствующая задача безусловной оптимизации записывается в следующем виде:
Решение. Приравняв две компоненты градиента L к нулю, получим


Для того чтобы проверить, соответствует ли стационарная точка х° минимуму, вычислим элементы матрицы Гессе функции L(х;u), рассматриваемой как функция х,
HL(x)= 
которая оказывается положительно определенной.
Это означает, что L(х,u) — выпуклая функция х. Следовательно, координаты x1 0 =λ, x2 0 =λ/2 определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x1 0 и x2 0 в уравнение2x1+x2=2, откуда 2λ+λ/2=2 или λ 0 =4/5. Таким образом, условный минимум достигается при x1 0 =4/5 и x2 0 =2/5 
При решении задачи из примера мы рассматривали L(х;λ) как функцию двух переменных x1и x2и, кроме того, предполагали, что значение параметра λ выбрано так, чтобы выполнялось ограничение. Если же решение системы

в виде явных функций λ получить нельзя, то значения х и λ находятся путем решения следующей системы, состоящей из n+1 уравнений с n+1 неизвестными:

Для нахождения всех возможных решений данной системы можно использовать численные методы поиска (например, метод Ньютона). Для каждого из решений ( 
Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств. Рассмотрим общую задачу, в которой требуется
при ограничениях hk =0, k=1, 2, . К.
Функция Лагранжа принимает следующий вид:
L(x,λ)=f(x)-
Здесь λ1, λ2, . λk —множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравнивая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными:
Если найти решение приведенной выше системы в виде функций вектора λ оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств
Решение расширенной системы, состоящей из n+К уравнений с n+К неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции L, рассматриваемой как функция х, подобно тому, как это было проделано в случае задачи с одним ограничением. Для некоторых задач расширенная система n+К уравнений с n+K неизвестными может не иметь решений, и метод множителей Лагранжа оказывается неприменимым. Следует, однако, отметить, что такие задачи на практике встречаются достаточно редко.
Рассмотрим частный случай общей задачи нелинейного программирования, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных и 



Данную задачу называют задачей на условный экстремум или классической задачей оптимизации.
Чтобы найти решение этой задачи, вводят набор переменных 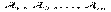

находят частные производные 

с n+m неизвестными 

Алгоритм метода множителей Лагранжа
1.Составляем функцию Лагранжа.
2.Находим частные производные от функции Лагранжа по переменным xJ,λi и приравниваем их нулю.
3.Решаем систему уравнений (7), находим точки, в которых целевая функция задачи может иметь экстремум.
4.Среди точек, подозрительных на экстремум, находим такие, в которых достигается экстремум, и вычисляем значения функции (6) в этих точках.
Исходные данные:По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве x1 изделий 1 способом затраты равны 4x1+x1 2 руб., а при изготовлении x2 изделий 2 способом они составляют 8x2+x2 2 руб. Определить сколько изделий каждым из способов следует изготовить, чтобы затраты на производство продукции были минимальными.
Целевая функция для поставленной задачи имеет вид
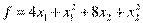
1.Составляем функцию Лагранжа

2. Вычисляем частные производные по x1, x2, λ и приравниваем их нулю:
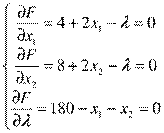
3. Решая полученную систему уравнений, находим x1=91,x2=89
4.Сделав замену в целевой функции x2=180-x1 , получим функцию от одной переменной, а именно f1=4x1+x1 2 +8(180-x1)+(180-x1) 2
Вычисляем 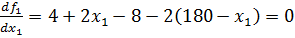
Ответ: Количество изделий изготовленных первым способом равно х1=91, вторым способом х2=89 при этом значение целевой функции равно 17278 руб.
💡 Видео
СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСкачать

Некоторые способы построения целевой функцииСкачать

Урок 1.Поиск решения, оптимизация, оптимальный план производстваСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение задачи линейного программирования при помощи надстройки Поиск решенияСкачать

Условный экстремум и функция ЛагранжаСкачать

Различие между уравнениями и функциямиСкачать

Линейное программирование 031138.mp4Скачать

Целевая функция в управлении Народными советамиСкачать

Линейное программирование Часть 1. Постановка задачиСкачать

Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.Скачать

Графический метод решения задач оптимизацииСкачать

Математика без Ху!ни. Экстремум функции 2х переменных.Скачать

Решение системы уравнения с помощью настройки поиск решенияСкачать
Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точкиСкачать

Минимизация целевой функции. Лекция 4.Скачать

Понятие функции. 7 класс.Скачать