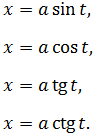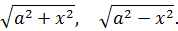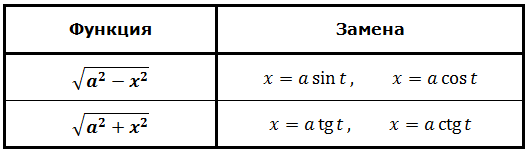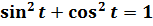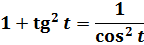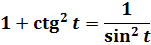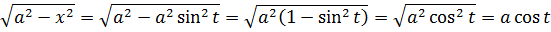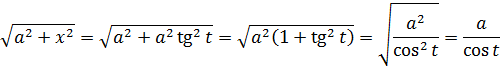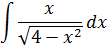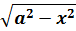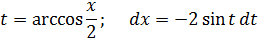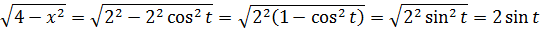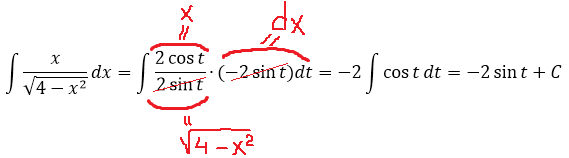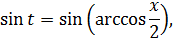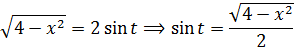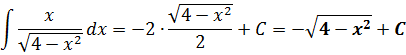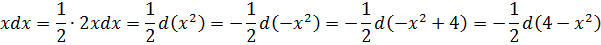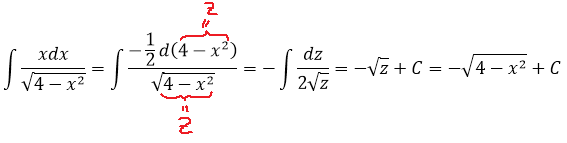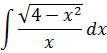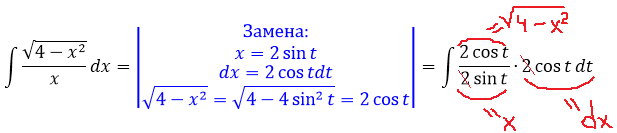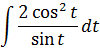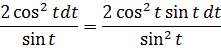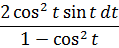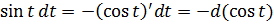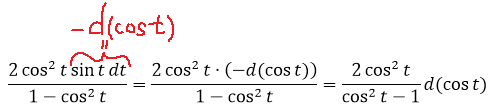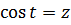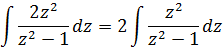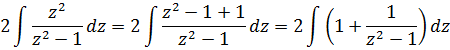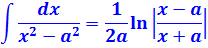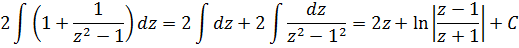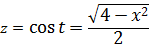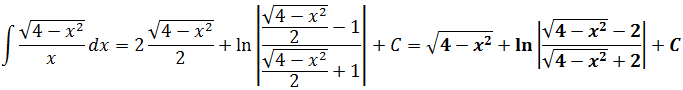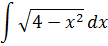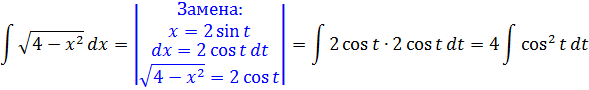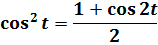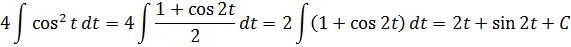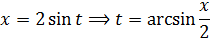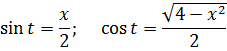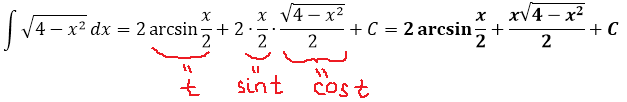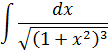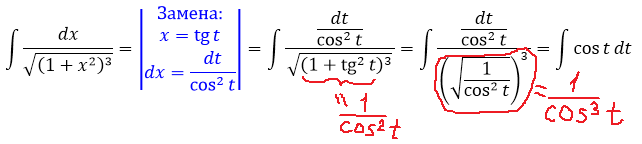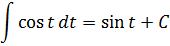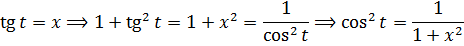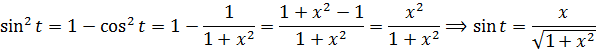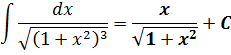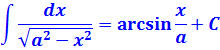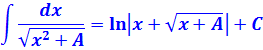Тригонометрические замены в иррациональных уравнениях (7 видео)

Тригонометрическая замена. Интегрируем квадратичные иррациональности!

Итак, друзья, продолжаем знакомиться с типовыми заменами при вычислении неопределённых интегралов. В прошлый раз мы познакомились с наиболее часто употребляемой степенной заменой, усвоили, как и где именно она применяется, порешали несложные примеры с корнями. Суть степенной замены заключалась в том, что старая переменная интегрирования икс заменялась степенной функцией от новой переменной t. И после такой замены у нас пропадали все корни.

В этом уроке речь пойдёт о так называемой тригонометрической замене. Суть её тоже очень простая и заключается в следующем: старая переменная икс заменяется на некоторую… тригонометрическую функцию от t. Да-да! Всего возможно четыре варианта:

Параметр а — некоторая положительная константа. Зачем она там нужна, станет ясно чуть ниже. На примерах.)

А теперь будем разбираться, где именно применяется такая замена и что она нам даёт. Заодно и элементарную тригонометрию повторим. 🙂

Тригонометрическая замена, так же, как и степенная, применяется при интегрировании некоторых функций с корнями. Только, в отличие от степенной замены, для тригонометрической есть два важных условия её применения:

1) Подынтегральная функция содержит квадратный (и только квадратный!) корень;

2) Под корнем стоит квадратичная конструкция вида a 2 ±x 2 .

Иными словами, в сегодняшнем уроке речь пойдёт о вычислении интегралов, содержащих вот такие корни:

Для плюса и для минуса используется своя замена. Вот вам небольшая сводная табличка:

Выбирать можно любую из предложенных подстановок: для минуса хоть синус, хоть косинус, а для плюса — либо тангенс, либо котангенс. Что больше нравится. 🙂

Суть тригонометрической замены полностью аналогична — убрать корень. То есть, добиться того, чтобы под корнем получился точный квадрат и корень извлекался начисто. И, тем самым, исчез из примера.)

Как же это происходит? Для полного понимания нам понадобится три до боли знакомых школьных тождества:

А теперь возьмём какой-нибудь из корней (пусть первый корень, с минусом в подкоренном выражении) и подставим в него нашу замену (допустим, с синусом a·sin t). Что у нас получится:

Для корня с плюсом проделаем всё то же самое, но на примере подстановки с тангенсом:

Вот и вся суть. Был корень — и нету корня! Возможно, кто-то хмыкнет скептически: какая, мол, разница, корень под интегралом или тригонометрия?! Хрен редьки не слаще… А в чём-то тригонометрия даже и похуже корней будет!

Что ж, настало время удивить скептиков. На примерах.) Итак, начнём!

Пример 1

Подынтегральная функция содержит корень вида

Число а у нас — двойка: 4 = 2 2 . Раз под корнем минус, то используем замену либо с синусом, либо с косинусом. Давайте, с косинусом возьмём. Для разнообразия.)

Итак, замена: x = 2cos t

Сразу же можно выразить само t, а также dx:

А теперь, используя нашу замену, упрощаем сам корень, который нам так мешает:

Вот и отлично. Корня больше нет. Теперь посмотрим, что же у нас получится под интегралом после такой замены:

И как вам? Был интеграл от ужасного корня, а после замены стал табличный (!) интеграл. От косинуса, правда, ну и что в этом страшного? 🙂

Осталось лишь вернуться обратно к переменной икс и записать ответ. Только я не буду сейчас тупо в лоб считать что-то типа

а сразу найду синус t из равенства, где мы упрощали наш корень:

Всё. Подставляем это выражение в наш результат вместо sin t и окончательно получаем:

И все дела.) Да-да, вот такой вот простенький ответ у этого примера.) Можете даже в уме его продифференцировать и получить подынтегральную функцию. 🙂

Особо глазастые студенты при первом взгляде на пример, возможно, узрели вот такую взаимосвязь:

Что ж, респект глазастым! 🙂 Да, действительно, если внести подкоренное выражение 4-х 2 под дифференциал, то пример элементарно сведётся к табличной степенной функции:

Можно так интегрировать? А почему — нет? Математика не запрещает. Но нам ведь размяться с тригонометрической заменой нужно! Вот и изучаем на несложном примере. 🙂

А теперь пример посложнее. Поменяем местами в нашей подынтегральной функции числитель и знаменатель. То есть, просто перевернём подынтегральную функцию. Вот такой пример будем решать:

Пример 2

Давайте, в этот раз используем замену с синусом. Сразу пишем:

И теперь, после подстановки, наш новый интеграл стал выглядеть вот так:

Что делать дальше? Главное — не бояться! И смекалки немного. 🙂

Вообще говоря, на такого рода функции есть свой приём интегрирования (тоже замена, кстати), но мы пока сделаем вид, что про неё не знаем. 🙂 И попробуем выкрутиться с помощью элементарных преобразований, которые мы с вами уже знаем. )

Что здесь можно сделать? Ну, напрашивается подведение под дифференциал, ибо в дроби сидят синус и косинус — родственнички по производной.) Для этого надо попробовать преобразовать подынтегральное выражение так, чтобы везде осталась одна функция — либо синус, либо косинус. Здесь можно всё свести к косинусу. Смотрите, как это делается! По пунктам:

1. Умножаем числитель и знаменатель дроби (вместе с dt!) на sin t. Что именно это даст — узнаем дальше.

2. Заменяем в знаменателе sin 2 t на 1-cos 2 t. Согласно основному тригонометрическому тождеству, ага. 🙂

и подводим косинус под знак дифференциала (про минус тоже не забываем, да).

Вот так. Теперь всё подынтегральное выражение у нас сведено к косинусу. Я согласен, что ещё надо было додуматься домножить всё на sin t, чтобы выйти на такую комбинацию. Но тут уже только богатый опыт рулит. Такое чутьё приходит только с практикой. Так что — решайте примеры! Чем больше, тем лучше.)

Итак, теперь смело заменяем косинус новой буквой. Тэ у нас уже использовано, пусть зэт будет:

Выражаем наш интеграл теперь уже через переменную z:

А теперь в дело вступает наш старый добрый излюбленный приёмчик — отнять/прибавить единичку. 🙂 Продолжаем:

Единичка, я надеюсь, ни у кого проблем в интегрировании не вызывает? А что же касается дроби 1/(z 2 -1), то это не что иное, как табличный интеграл! Открывайте нашу таблицу и ищите похожую формулу. Это седьмая формула, с «высоким» логарифмом:

В роли «а» у нас выступает единичка. Возвращаемся к нашим баранам:

Что ж, заготовка для ответа получена. Теперь поэтапно возвращаемся обратно к иксу:

Вот такой вот интересный пример. И довольно красивый ответ.)

Маньяки могут его продифференцировать. Я продифференцировал. Всё гуд.)

Продолжаем развлекаться. 🙂 Теперь вообще уберём знаменатель и решим вот такой примерчик:

Пример 3

Под интегралом теперь стоит просто чистый корень, безо всего. И тут тоже на помощь придёт тригонометрическая замена.) Давайте, снова будем всё выражать через синус, ибо он удобнее: минус лишний не всплывает, который легко потерять. Действуем:

Как теперь быть с косинусом в квадрате? Если в прошлом примере нам пришлось домножать всё на синус, то тут всё гораздо проще. Призываем на помощь школьную тригонометрию! На сей раз — формулы понижения степени. А чуть конкретнее — вот эту:

И после такого преобразования наш интеграл легко превращается в сумму табличных (ну, или почти табличных :)):

Надеюсь, особо не нужно комментировать, как именно при интегрировании получился синус двух t? Кто не понял — читаем урок « Подведение функции под знак дифференциала ». Там всё популярно изложено. 🙂

Всё. «Рыба» для ответа готова. Осталось правильно перейти к иксу да подставить вместо t в выражения 2t и sin 2t.

Прежде всего, выясним из нашей замены, что же такое это самое t:

Теперь раскроем синус двойного угла: sin2t = 2sin t·cos t

Зачем так сделано? А затем, что теперь и синус и косинус легко выражаются через x (смотрим синюю табличку с нашей заменой)! Вот так:

И теперь наш окончательный ответ полностью готов:

Ну как? Да, я согласен, не самые простые примеры. Так и мы с вами уже всё-таки на приличном уровне, правда?

Что-то мы всё с синусами да косинусами возимся, а тангенс/котангенс как-то обделили вниманием. Давайте и такой примерчик рассмотрим! На десерт.) Он совсем несложный: хватит с вас жести на сегодня! 🙂 Просто чтобы суть замены уловить.)

Пример 4

Не пугаемся внешнего вида примера! Внешность иногда бывает обманчива, да.)

Сразу замечаем под корнем сумму 1+х 2 . Раз сумма, то, стало быть, подходящая замена для ликвидации корня — с тангенсом (или котангенсом). Опять же, по причине нежелания возиться с лишним минусом, я выберу тангенс (а = 1, x = tg t):

И снова перед нами безобидный табличный интеграл! Интегрируем косинус и — готово дело:

Всё. Выражаем теперь нашу первообразную через икс. Как? По формулам тригонометрии, вестимо! У нас есть тангенс, а нас интересует синус.

Так. Квадрат косинуса готов. Осталось лишь из основного тригонометрического тождества вытащить квадрат синуса, извлечь корень и — цель достигнута!

Вот и наш ответ. Довольно простенький на сей раз:

Подытожим наш урок. Давайте разберёмся, зачем в самом начале урока я высказал два обязательных требования, чтобы сам корень был только квадратным (а не кубическим или какой-то более высокой степени), а также чтобы под корнем находилась конструкция вида x 2 ±a 2 . Догадались, почему?

Да потому, что в любой другой ситуации (кубический корень или же под корнем многочлен более высокой степени) у нас просто-напросто не исчезнет иррациональность, и данная замена нам уже никак не поможет свести интеграл к красивому виду. 🙂 И, если вам, вдруг, попался такой пример, то, скорее всего, преобразования более хитрые.

Разумеется, подобные интегралы не ограничиваются этими четырьмя примерами. И для интегралов, содержащих квадратичные иррациональности, есть и более суровые подстановки — Эйлера и Абеля. Но такие подстановки — уже высший пилотаж в интегрировании. Их мы будем изучать ближе к концу раздела. Зато тщательный разбор этих четырёх примеров даст вам возможность уверенно брать хотя бы некоторые интегралы подобного типа. Так что тригонометрическая замена — штука весьма полезная. Мы с ней дружить будем. 🙂 А для дружбы, конечно же, необходимо хорошо знать школьную тригонометрию — основные тождества (их шесть), двойные углы, формулы понижения степени и т.д.

Что ж, на сегодня хватит. А в качестве тренировочного упражнения в этот раз я дам небольшое творческое задание. Чтобы скучно не было.)

Есть в нашей замечательной табличке интегралов парочка довольно страшных формул. Вот эти:

И теперь, в качестве задания, я предлагаю вам доказать эти формулы! С помощью тригонометрической замены, да.) Чтобы вы прочувствовали, откуда что в математике берётся. И берётся явно не с потолка.)

С первой формулой проблем возникнуть не должно: там всё очевидно. А вот со второй («длинным логарифмом») я немного подскажу. В формуле число А для определённости предполагается положительным. Раз оно положительное, то можно совершенно спокойно заменить это самое А на a 2 . И дальше работать уже с заменой через тангенс.) Материала этого (и прошлых) уроков вполне достаточно, чтобы одолеть это задание. Будет вам там парочка сюрпризов! Выручат свойства логарифмов и первообразных (это подсказка! :)).

Содержание

Алгебра
Иррациональные уравнения
Простейшие иррациональные уравнения
Уравнения с двумя квадратными корнями
Введение новых переменных
Замена иррационального уравнения системой
Уравнения с «вложенными» радикалами
Иррациональные неравенства
Тригонометрические замены в иррациональных уравнениях
💥 Видео

Видео:Решение иррационального уравнения с помощью тригонометрической заменыСкачать

Алгебра

План урока:

Видео:Решение иррационального уравнения с помощью тригонометрической заменыСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:Решение иррациональных уравнений: метод заменыСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:Система тригонометрических уравнений. Или иррациональных?Скачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Тригонометрические замены в иррациональных уравнениях

1. Уравнение вида $$ sqrt = g(x) $$

Решение: Решением уравнения $$ sqrt = g(x) $$ будет решение равносильной системы $$ left< begin g(x) ge 0; \ f(x) = g^2 (x). \ end right.$$

2. Уравнение вида $$ sqrt cdot g(x) = 0$$

Решение: Решением уравнения $$ sqrt cdot g(x) = 0$$ будет решение равносильной совокупности систем $$ left< begin f(x) = 0; \ g(x) — ,определена. \ end right. $$ или $$ left< begin g(x) = 0; \ f(x) ge 0. \ end right. $$

3. Уравнение вида $$ sqrt = sqrt $$

Решение: Решением уравнения $$ sqrt = sqrt $$ будет решение одной из равносильных систем $$ left< begin f(x) = g(x); \ f(x) ge 0. \ end right.$$ или $$ left< begin f(x) = g(x); \ g(x) ge 0. \ end right. $$

4. Уравнение вида $$ sqrt cdot sqrt = 0$$

Решение: Решением уравнения $$ sqrt cdot sqrt = 0$$ будет решение равносильной совокупности систем $$ left< begin f(x) = 0; \ g(x) ge 0. \ end right.$$ или $$ left< begin g(x) = 0; \ f(x) ge 0. \ end right.$$

5. Уравнение вида $$ sqrt[3]<> + sqrt[3]<> = sqrt[3]<>$$

Решение: Решением уравнения $$ sqrt[3]<> + sqrt[3]<> = sqrt[3]<>$$ будет решение равносильной совокупности систем $$ left< begin f(x) = 0; \ f;и;g, — ,определены. \ end right. $$ или $$ left< begin g(x) = 0; \ f;и;g, — ,определены. \ end right. $$ или $$ left< begin f(x) + g(x) = 0; \ f;и;g, — ,определены. \ end right.$$.

6. Уравнение вида $$ sqrt[n]<> + sqrt[n]<> = g(x)$$

Решение: Решение уравнения $$ sqrt[n]<> + sqrt[n]<> = g(x)$$ после замены переменных $$ left< begin sqrt[n]<> = h,,, ge 0; \ sqrt[n]<> = t,,, ge 0. \ end right. $$ сводится к решению системы алгебраических уравнений $$ left< begin h + t = g(x); \ h^n + t^n = a + b. \ end right.$$.

7. Уравнение вида $$ sqrt pm sqrt = b$$

Решение: Решение уравнения $$ sqrt pm sqrt = b$$ сводится к решению иррационального уравнения вида $$ sqrt = frac<><> $$.