Тригонометрические уравнения с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Видео:Тригонометрическое уравнение: cos(z)=2, а при чём тут формула Эйлера?Скачать

Примеры решений задач с комплексными числами

На этой странице вы найдете подробные готовые задания с ответами по разделу «Комплексные числа»: действия с комплексными числами, преобразование в алгебраическую, тригонометрическую и показательную форму, возведение в степень и извлечение корня по формуле Муавра, решение уравнений с комплексными корнями и т.п.

Если вам нужна помощь в выполнении работы по комплексным числам, мы будем рады помочь: стоимость задания от 70 рублей, срок от 1 дня, гарантия месяц, подробное оформление (см. Решение задач на заказ).

Еще полезные ссылки для изучения:

Видео:Тригонометрическая форма комплексного числаСкачать

Графические задачи с комплексными числами

Задача 1. Найдите геометрическое место точек, изображающих $z$, удовлетворяющих системе неравенств: $$ |z-1| lt 1, \ Re z le 1, \ Im z le 1.$$

Задача 2. Изобразите на $C$: $Re z^2 =-1$.

Видео:Комплексные числа и "золотое" уравнениеСкачать

Действия с комплексными числами. Решения задач

Задача 3. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости. $$ z_1 = 2 e^, z_2=4 e^.$$

Задача 4. Вычислить произведение $z_1 cdot z_2$ и частное $z_1 / z_2$ комплексных чисел. Операнды и результаты изобразить на комплексной плоскости. $$ z_1 = 4+3i, z_2=1-sqrt i.$$

Задача 5. Найти все значения корней из заданного комплексного числа $sqrt[4].$

Задача 6. Вычислить $left(frac right)^.$ Представить результат в алгебраической и показательной формах.

Видео:Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

Формы комплексных чисел. Решения задач

Задача 7. Найти $|z|$, $arg z$, записать число $z$ в тригонометрической и показательной форме $z=-sqrt-i.$

Задача 8. Найдите $z$ в тригонометрической форме, если $z=(3-3isqrt)(5sqrt+5i).$

Задача 9. Дано комплексное число $a$. Требуется:
1) записать число $a$ в алгебраической и тригонометрической формах;
2) найти корни уравнения $z^3+a=0$. $$a=frac<sqrt-i>.$$

Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Уравнения с комплексными числами. Решения задач

Задача 10. Решите уравнение (ответ запишите в алгебраической форме): $sh z — ch z =2i.$

Задача 11. Решить уравнения или вычислить: $$ frac = frac. $$

Задача 12. Найти все комплексные корни заданного уравнения, отметить найденные корни на комплексной плоскости: $z^6-7z^3-8=0.$

Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

где $left| z right|$ — модуль комплексного числа, $text!!varphi!!text$ — некоторый угол, который называется аргумент комплексного числа (пишут $text!!varphi!!text=arg left( z right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=sqrt+i$.

Переписываем исходное число в виде $z=sqrt+1cdot i$ и считаем модуль:

Выносим модуль за скобки:

[z=sqrt+1cdot i=2cdot left( frac<sqrt>+fraccdot i right)]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $frac<text!!pi!!text>$ с тем же успехом можно взять аргумент $frac<13text!!pi!!text>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

[begin & <_>=left| <_> right|cdot left( cos alpha +isin alpha right) \ & <_>=left| <_> right|cdot left( cos beta +isin beta right) \ end]

Тогда их произведение равно

[<_>cdot <_>=left| <_> right|cdot left| <_> right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]

А если ещё и $left| <_> right|ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

[begin <_>cdot <_> & =2cdot 5cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)= \ & =10cdot left( cos frac+isin frac right) \ end]

[begin frac<<_>><<_>> & =fraccdot left( cos left( frac-frac right)+isin left( frac-frac right) right)= \ & =0,4cdot left( cos frac+isin frac right) \ end]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

Видео:Изобразить область на комплексной плоскостиСкачать

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

Возведём его в квадрат, умножив на само себя:

[begin <^> & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text!!varphi!!text!!varphi!!text right)+isin left( text!!varphi!!text!!varphi!!text right) right)= \ & =<^>cdot left( cos 2text!!varphi!!text+isin 2text!!varphi!!text right) \ end]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

[z=left| z right|cdot left( cos varphi +isin varphi right)]

в степень $nin mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

[begin sqrt-i & = 2cdot left( frac<sqrt>+icdot left( -frac right) right)= \ & =2cdot left( cos left( -frac right)+isin left( -frac right) right) \ end]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

4. Дополнение 1. Геометрический подход

Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

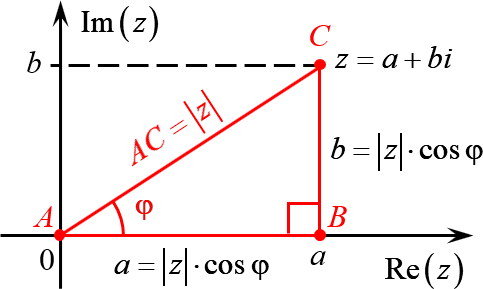
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:

[begin & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

[begin a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end]

Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

Видео:3. Тригонометрическая форма комплексного числаСкачать

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $varphi =pi $ (синяя точка $B$).
• На положительной полуоси ординат $varphi =frac$ (зелёная точка $B$).
• На отрицательной — $varphi =frac$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<_>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:

[begin 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatornamefrac end]

Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:

[6-6i=6sqrtcdot left( cos left( -frac right)+isin left( -frac right) right)]

В левой полуплоскости откладываем от луча, соответствующего углу $pi $:

Итого для точки $Cleft( -2;5 right)$ имеем:

[begin -2+5i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi -operatornamefrac end]

И, наконец, для точки $Dleft( -5;-3 right)$:

[begin -5-3i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi +operatornamefrac end]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

🎦 Видео

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Комплексные числа в уравненияхСкачать

Математика без Ху!ни. Комплексные числа, часть 2. Простейшие действия.Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Высшая математика. Комплексные числаСкачать

4. Показательная форма комплексного числаСкачать

Перевод комплексного числа из алгебраической формы в тригонометрическую, показательнуюСкачать

Уравнение с комплексными числамиСкачать

Комплексные корни квадратного уравненияСкачать