Когда мы решаем сложное тригонометрическое уравнение в ЕГЭ по математике, то рассчитываем получить красивые корни, их которых легко отбираются итоговые значения на отрезке. И обычно корни действительно оказываются красивыми.
Но что делать, если получился какой-нибудь арктангенс? Или арксинус? Как грамотно отметить их на тригонометрическом круге и в итоге безошибочно отобрать корни на отрезке? Что ж, попробуем разобраться.
Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать
Решение простейших тригонометрических уравнений с помощью аркфункций
Готовиться с нами — ЛЕГКО!
Видео:Отбор корней с аркфункциями в №12 | Это будет на ЕГЭ 2023 по математикеСкачать
Эффективное решение существует!
Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.
Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Задача 1
Решите уравнение [sin x=-a, quad 0
Решение
(arcsin(-a)) – это такой угол из отрезка (left[-dfrac2; dfrac2right]) , синус которого равен (-a) :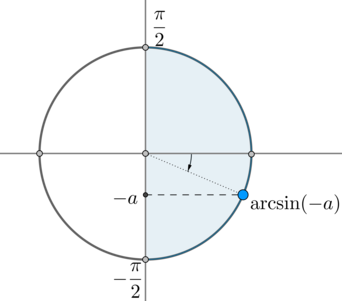 
Следовательно, одна серия решений данного уравнения – это (x=arcsin(-a)+2pi n, ninmathbb) .
Но на окружности есть еще одна точка, синус в которой равен (-a) – угол (alpha) :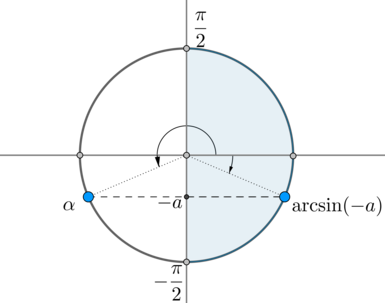 
Заметим, что (alpha=pi+(-arcsin(-a))) . Так как (arcsin(-a)=-arcsin a) , то (alpha=pi+arcsin a) . Следовательно, ответ в нашем уравнении: [left[beginbegin &x=-arcsin a+2pi n, ninmathbb\[2ex] &x=pi+arcsin a+2pi k, kinmathbbendendright.]
Задача 2
Решите уравнение [cos x=-a, quad 0
Решение
(arccos(-a)) – это такой угол из отрезка (left[0; piright]) , косинус которого равен (-a) :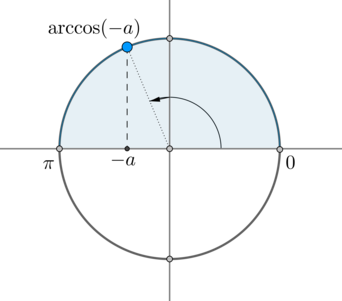 
Следовательно, одна серия решений данного уравнения – это (x=arccos(-a)+2pi n, ninmathbb) .
Но на окружности есть еще одна точка, косинус в которой равен (-a) – угол (alpha) :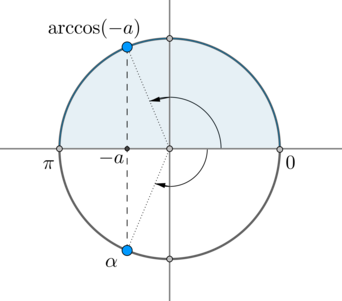 
Заметим, что (alpha=-arccos(-a)) . Так как (arccos(-a)=pi-arccos a) , то (alpha=-pi+arccos a) . Следовательно, ответ в нашем уравнении: [left[beginbegin &x=pi-arccos a+2pi n, ninmathbb\[2ex] &x=-pi+arccos a+2pi k, kinmathbbendendright.]
Задача 3
Решите уравнение [mathrm, x=-a, a>0]
Решение
(mathrm,(-a)) – это такой угол из промежутка (left(-dfrac2;dfrac2right)) , тангенс которого равен (-a) :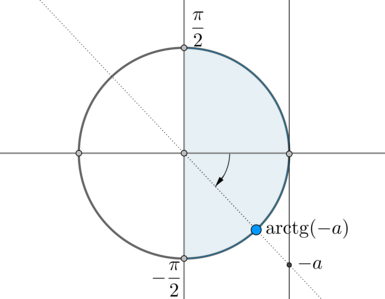 
Следовательно, одна серия решений данного уравнения – это (x=mathrm,(-a)+2pi n, ninmathbb) .
Но на окружности есть еще одна точка, тангенс в которой равен (-a) – угол (alpha) :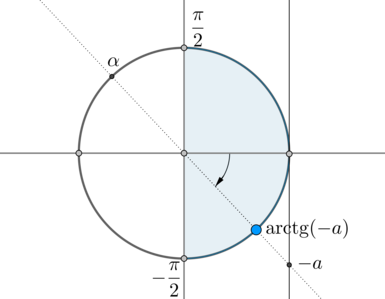 
Заметим, что (alpha=mathrm,(-a)+pi) . Так как (mathrm,(-a)=-mathrm, a) , то (alpha=pi-mathrm, a) . Следовательно, ответ в нашем уравнении: [left[beginbegin &x=-mathrm, a+2pi n, ninmathbb\[2ex] &x=pi-mathrm, a+2pi k, kinmathbbendendright.] Заметим, что так как углы (-mathrm, a) и (pi-mathrm, a) отличаются друг от друга на (pi) , то ответ можно записать в виде одной серии корней с периодом (pi) : [x=-mathrm, a+pi m, minmathbb]
Задача 4
Решите уравнение [mathrm, x=-a, a>0]
Решение
(mathrm,(-a)) – это такой угол из промежутка (left(0;piright)) , котангенс которого равен (-a) :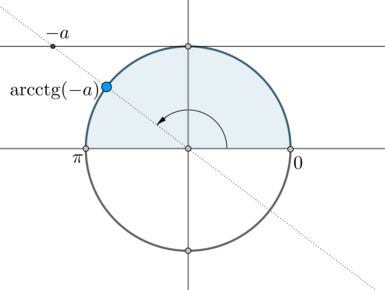 
Следовательно, одна серия решений данного уравнения – это (x=mathrm,(-a)+2pi n, ninmathbb) .
Но на окружности есть еще одна точка, котангенс в которой равен (-a) – угол (alpha) :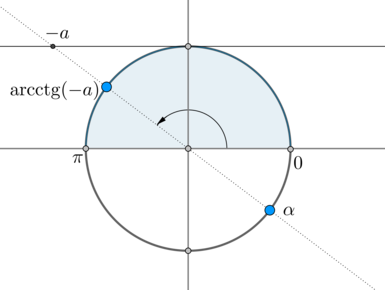 
Заметим, что (alpha=mathrm,(-a)+pi) . Так как (mathrm,(-a)=pi-mathrm, a) , то (alpha=2pi-mathrm, a) . Следовательно, ответ в нашем уравнении: [left[beginbegin &x=pi-mathrm, a+2pi n, ninmathbb\[2ex] &x=2pi-mathrm, a+2pi k, kinmathbbendendright.] Заметим, что так как углы (2pi-mathrm, a) и (pi-mathrm, a) отличаются друг от друга на (pi) , то ответ можно записать в виде одной серии корней с периодом (pi) : [x=pi-mathrm, a+pi m, minmathbb]
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка , синус которого равен . Да, это
| 0 |
| 0 |
Строим график функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при
5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что
| 0 |
| 0 |
Вот график арккосинуса:
1. Область определения
2. Область значений
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
📽️ Видео
Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать
Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать
Арк-функции. Простейшие тригонометрические уравнения | Осторожно, спойлер! | Борис Трушин !Скачать
Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать
Решение тригонометрических уравнение в ЕГЭ для новичков | ЕГЭ Математика | Аня Матеманя | ТопскулСкачать
Аркфункции, разложение на множители - Задание №13 из ЕГЭ - Тригонометрические уравнения (часть 1)Скачать
САМЫЕ СЛОЖНЫЕ Задания #6 ЕГЭ 2024 (Тригонометрические Уравнения) | Школа ПифагораСкачать
3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать
ЕГЭ-ПРОФИЛЬ. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ЗАДАНИЕ-12Скачать
Задание 13 ЕГЭ отбор с арксинусомСкачать
КОГДА ПИСАТЬ +Пк, а когда +2Пк? (Задание 13 по Тригонометрии ЕГЭ 2024 по Математике Профиль)Скачать
Отбор арктангенса по окружности | Тригонометрия ЕГЭ 2020Скачать
Тригонометрические уравнения. Задание 12 | Профильная математика ЕГЭ 2023 | УмскулСкачать
Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать
Решение тригонометрических уравнений №12 | Математика ЕГЭ 2023 | УмскулСкачать
