Тригонометрические уравнения приводимые к квадратным самостоятельная работа

Класс: 11

Презентация к уроку

Цели и задачи урока.

• Образовательные:
  • повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения
  • сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к квадратным.
  • уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к квадратным и решать их.
• Развивающие:
  • развивать логическое мышление учащихся, память, внимание, речь; умения рассуждать и выделять главное; умение самостоятельно приобретать знания и применять их на практике, развивать навыки самоконтроля и взаимоконтроля.
• Воспитательные:
  • воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.

Оборудование: мультимедийный проектор, экран, лист самооценки.

Организационные формы общения: фронтальная, групповая, индивидуальная.

Тип урока: усвоения новых знаний.

Образовательные технологии: ИКТ, проектная.

План урока.

1. Организационный момент, формирование мотивации работы учащихся.
2. Формулирование темы, цели урока.
3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала.
4. Этап усвоения новых знаний и способов действий.
5. Этап активной релаксации и активизации.
6. Этап первичной проверки понимания изученного.
7. Этап рефлексии и оценивания. Подведение итогов урока.
8. Этап информирования учащихся о домашнем задании, инструктаж по его выполнению.

Подготовительная работа

Учащихся класса необходимо заранее поделить на группы. Принцип деления учащихся на группы учитель вправе выбрать самостоятельно.
Один из вариантов – группы, в которые вошли бы учащиеся с разным уровнем математической подготовки: от «базового» до «продвинутого».
Каждая группа предварительно получает задание изучить алгоритм решения одного из типов тригонометрических уравнений (используются предложенные учителем источники информации и самостоятельно найденные). Результаты своей работы члены каждой группы представляют на одном из уроков по теме «Тригонометрические уравнения». В зависимости от объёма предлагаемого материала и его сложности одном уроке могут успеть выступить 1-2 группы, представив результаты своей работы.
Предлагаем вашему вниманию урок, на котором рассматривается решение тригонометрических уравнений, сводящихся к квадратным.

Из дома реальности легко забрести в лес математики, но лишь немногие способны вернуться обратно.

Чем больше человек будет становиться человеком, тем меньше он согласится на что-либо иное, кроме бесконечного и неистребимого движения к новому.

1. Организационный момент, формирование мотивации работы учащихся (3 мин.)

Приветствие. Фиксация отсутствующих, проверка готовности учащихся к уроку. Далее каждому ученику выдаётся оценочный лист. Учитель кратко комментирует правила заполнения оценочного листа и предлагает заполнить 1-3 строки. Приложение 1.
Организация внимания учащихся: учитель цитирует учащимся Пьера Шардена, предлагает пояснить, как они поняли смысл слов (можно выслушать 2-3 человека), предлагает сделать слова девизом урока и интересуется, знают ли они, кто является их автором. Краткая историческая справка (Слайд 3).

*Инструкция по использованию Презентации – Приложение 2.

2. Формулирование темы, цели урока (2-3 мин.).

Учитель просит сформулировать тему предыдущего урока (Решение простейших тригонометрических уравнений). Интересуется у учащихся, как они думают, существуют ли другие типы тригонометрических уравнений? (Да. Если есть «простейшие», то значит, есть более сложные, иначе нет необходимости вводить термин «простейшие», если это единственный тип тригонометрических уравнений). Исходя из выше сказанного, предлагает сформулировать тему сегодняшнего урока (Решение сложных/других/различных типов тригонометрических уравнений).
После корректировки темы, предлагает учащимся записать в их тетрадях: дату проведения урока, фразу «Классная работа» и тему урока «Решение различных типов тригонометрических уравнений: уравнения, сводящиеся к квадратным».
На столе у каждого из учащихся находятся шаблоны яблок и фломастеры. Предлагается написать на «яблоках» свои ожидания от предстоящего урока, тему которого уже сформулировали. После этого все шаблоны яблок прикрепляются, например, с помощью скотча на заранее приготовленный плакат с изображением дерева. Получается «Дерево ожиданий».

По мере достижения того или иного ожидания соответствующее яблоко можно считать созревшим и собирать в корзину. Использование этого активного метода обучения – наглядный способ отслеживания продвижения учащихся на уроке. [1]

Возможен другой вариант: учитель ставит песочные часы перед учениками класса и предлагает ответить на вопрос о том, чему они хотят научиться на уроке, тема которого уже сформулирована (достаточно 1-2 варианта).

3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала (10 мин.).

Учитель. Герберт Спенсер говорил, что если знания человека в беспорядочном состоянии, то чем больше их у него, тем сильнее расстраивается его мышление. Последуем совету этого известного британского философа (информация для общего развития личности – краткая историческая справка. (Слайд 5) Прежде чем перейти к изучению нового материала, давайте вспомним, что мы знаем из раздела «Тригонометрия».

Фронтальная работа (устно)

– Дайте определение тригонометрического уравнения.
– Сколько корней может иметь тригонометрическое уравнение?
– Что такое простейшие тригонометрические уравнения?
– Что значит решить простейшее тригонометрическое уравнение?
– Какие способы решения тригонометрических уравнений вы знаете? (2 варианта: формулы; единичная окружность).

а) Заполните таблицу:

б) Поставьте в соответствие уравнениям их решения, представленные на единичных окружностях (с комментарием)

С последующей взаимопроверкой/самопроверкой (правильность ответов проверяется с помощью презентации) на умение решать простейшие тригонометрические уравнения. Демонстрируется (Слайд 12). При необходимости решения некоторых уравнений коротко комментируются.

4. Этап усвоения новых знаний и способов действий (15 мин.).

Учащиеся класса предварительно были поделены на группы, каждая из которых самостоятельно рассмотрела, используя материал рекомендуемый учителем и найденный самостоятельно, один из типов тригонометрических уравнений.
Результаты работы оформляются в виде некой рекомендации/алгоритма/схемы решения в формате презентации Power Point. Учитель в случае необходимости консультирует учащихся групп и предварительно проверяет итоговый продукт их работы.
Для презентации результатов того или иного способа решения на уроке выбирается один из представителей группы, остальные на уроке помогают отвечать на возникающие вопросы по решению данного типа тригонометрического уравнения. Учащиеся заранее знакомятся с критериями оценивания своей работы в группе.

Мне приходится делить время
между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важней.
Политика существует только для данного момента,
а уравнения будут существовать вечно.

Возможные варианты выполнения задания группой. (Слайды 14-18)

1 группа. Решение тригонометрических уравнений, сводящихся к квадратным.

Отличительные признаки уравнений, сводящихся к квадратным:

1. В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.
2. В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.

Алгоритм решения:

– Используются ниже приведённые тождества; с их помощью необходимо выразить одну тригонометрическую функцию через другую:

– Выполняется подстановка.
– Выполняется преобразование выражения.
– Вводится обозначение (например, sinx = y).
– Решается квадратное уравнение.
– Подставляется значение обозначенной величины, и решается тригонометрическое уравнение.

Пример 1

6cos 2 x + 5 sin x – 7 = 0.

Пример 2

Пример 3

5. Этап активной релаксации и активизации (2 мин.).

Авторы метода: С. Казаков, Ю. Долинова. Приложение 4 (текст), слайды 20-25.

6. Этап первичной проверки понимания изученного (8 мин.)

Самостоятельная работа (Приложение 5)

Работа дифференцированная, каждый уровень сложности заданий представлен в двух вариантах.
I уровень – «3», II уровень – «4», III уровень – «5» в случае полного правильного решения. Работа будет проверена учителем к следующему уроку, отметки будут выставлены за урок.

7. Этап рефлексии и оценивания. Подведение итогов урока (2 мин.).

8. Этап информирования учащихся о домашнем задании, инструктаж по его выполнению (2 мин.).

Дифференцированное (раздаётся каждому ученику на отдельных листах) – Приложение 6

Список литературы:

1. Корнилов С.В., Корнилова Л.Э. Методический ларец. – Петрозаводск: ПетроПресс, 2002. – 12 с.

Видео:Тригонометрические уравнения сводящиеся к квадратнымСкачать

Самостоятельная работа по теме «Тригонометрические уравнения , сводящиеся к квадратным»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12 sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 1

1) 6 cos ² x — 7 cosx -5 = 0;

2) cos 2x – 3 cos x + 2=0;

3) 2 sin 4 x + 3 cos 2x +1=0.

Самостоятельная работа по теме: «Решение тригонометрических уравнений сводящихся к квадратным» вариант 2

1) 4 sin 2 x – 12sin x + 5 = 0;

2) cos 2x + 3 sin x – 2 = 0;

3) 4 cos 2 x + 4 cos( +x) – 1 = 0.

+ к, кϵΖ

2 к, кϵΖ

± + 2 к, кϵΖ

±

+

+ к, кϵΖ

+

+

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 939 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 587 485 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

§ 18. Тригонометрические уравнения

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 10.03.2021
• 96
• 11

• 10.03.2021
• 131
• 5

• 10.03.2021
• 100
• 2

• 10.03.2021
• 128
• 1

• 10.03.2021
• 115
• 0

• 10.03.2021
• 202
• 7

• 10.03.2021
• 242
• 2

• 10.03.2021
• 646
• 39

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 10.03.2021 1002
• DOCX 18.5 кбайт
• 78 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Биктанова Рита Альфитовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 6 месяцев
• Подписчики: 2
• Всего просмотров: 158367
• Всего материалов: 114

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

В Швеции запретят использовать мобильные телефоны на уроках

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

Видео:Тригонометрические уравнения, сводящиеся к квадратным. 10 классСкачать

Практическая работа по теме: «Тригонометрические уравнения, сводящиеся к квадратным»

Практическая работа по теме: «Тригонометрические уравнения, сводящиеся к квадратным»

Просмотр содержимого документа
«Практическая работа по теме: «Тригонометрические уравнения, сводящиеся к квадратным»»

Тригонометрические уравнения, сводящиеся к квадратным

Цель работы: отработка умений и навыков решения тригонометрических уравнений, сводящихся к квадратным.

Отличительные признаки уравнений, сводящихся к квадратным:

1. В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.
2. В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.

– Используются ниже приведённые тождества; с их помощью необходимо выразить одну тригонометрическую функцию через другую:

–Выполняется преобразование выражения.

–Вводится обозначение (например, sinx = y).

–Решается квадратное уравнение.

–Подставляется значение обозначенной величины, и решается тригонометрическое уравнение.

Задания для самостоятельного выполнения

1. sin 2 x – 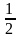sinx = 0

2. 5sin 2 x – cosx – 5 = 0

3. sin 2 x + 4cosx – 3 = 0

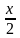
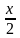
4. ctg 2 + 2ctg = 5

1. cos 2 x + 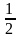cosx =0

📽️ Видео

Алгебра 10 класс Уравнения,сводящиеся к квадратнымСкачать

Тригонометрические уравнения, приводимые к квадратным и однородныеСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Тригонометрические уравнения, приводимые к квадратным | Алгебра 10 классСкачать

Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Тригонометрические уравнения, сводящиеся к квадратным.Скачать

тригонометрические уравнения, сводимые к квадратнымСкачать

ЕГЭ. Математика профильная. Задание 12. Тригонометрические уравнения сводящиеся к квадратным.Скачать

Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

Решение тригонометрических уравнений. 10 класс.Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрические уравнения. Задание 12 | Профильная математика ЕГЭ 2023 | УмскулСкачать

Тригонометрические уравнения которые сводятся к алгебраическим. Метод: замены переменных.Скачать

Тригонометрические уравнения, сводящиеся к квадратнымСкачать