Итак, друзья, продолжаем знакомиться с типовыми заменами при вычислении неопределённых интегралов. В прошлый раз мы познакомились с наиболее часто употребляемой степенной заменой, усвоили, как и где именно она применяется, порешали несложные примеры с корнями. Суть степенной замены заключалась в том, что старая переменная интегрирования икс заменялась степенной функцией от новой переменной t. И после такой замены у нас пропадали все корни.
В этом уроке речь пойдёт о так называемой тригонометрической замене. Суть её тоже очень простая и заключается в следующем: старая переменная икс заменяется на некоторую… тригонометрическую функцию от t. Да-да! Всего возможно четыре варианта:
Параметр а — некоторая положительная константа. Зачем она там нужна, станет ясно чуть ниже. На примерах.)
А теперь будем разбираться, где именно применяется такая замена и что она нам даёт. Заодно и элементарную тригонометрию повторим. 🙂
Тригонометрическая замена, так же, как и степенная, применяется при интегрировании некоторых функций с корнями. Только, в отличие от степенной замены, для тригонометрической есть два важных условия её применения:
1) Подынтегральная функция содержит квадратный (и только квадратный!) корень;
2) Под корнем стоит квадратичная конструкция вида a 2 ±x 2 .
Иными словами, в сегодняшнем уроке речь пойдёт о вычислении интегралов, содержащих вот такие корни:
Для плюса и для минуса используется своя замена. Вот вам небольшая сводная табличка:
Выбирать можно любую из предложенных подстановок: для минуса хоть синус, хоть косинус, а для плюса — либо тангенс, либо котангенс. Что больше нравится. 🙂
Суть тригонометрической замены полностью аналогична — убрать корень. То есть, добиться того, чтобы под корнем получился точный квадрат и корень извлекался начисто. И, тем самым, исчез из примера.)
Как же это происходит? Для полного понимания нам понадобится три до боли знакомых школьных тождества:
А теперь возьмём какой-нибудь из корней (пусть первый корень, с минусом в подкоренном выражении) и подставим в него нашу замену (допустим, с синусом a·sin t). Что у нас получится:
Для корня с плюсом проделаем всё то же самое, но на примере подстановки с тангенсом:
Вот и вся суть. Был корень — и нету корня! Возможно, кто-то хмыкнет скептически: какая, мол, разница, корень под интегралом или тригонометрия?! Хрен редьки не слаще… А в чём-то тригонометрия даже и похуже корней будет!
Что ж, настало время удивить скептиков. На примерах.) Итак, начнём!
Пример 1
Подынтегральная функция содержит корень вида
Число а у нас — двойка: 4 = 2 2 . Раз под корнем минус, то используем замену либо с синусом, либо с косинусом. Давайте, с косинусом возьмём. Для разнообразия.)
Итак, замена: x = 2cos t
Сразу же можно выразить само t, а также dx:
А теперь, используя нашу замену, упрощаем сам корень, который нам так мешает:
Вот и отлично. Корня больше нет. Теперь посмотрим, что же у нас получится под интегралом после такой замены:
И как вам? Был интеграл от ужасного корня, а после замены стал табличный (!) интеграл. От косинуса, правда, ну и что в этом страшного? 🙂
Осталось лишь вернуться обратно к переменной икс и записать ответ. Только я не буду сейчас тупо в лоб считать что-то типа
а сразу найду синус t из равенства, где мы упрощали наш корень:
Всё. Подставляем это выражение в наш результат вместо sin t и окончательно получаем:
И все дела.) Да-да, вот такой вот простенький ответ у этого примера.) Можете даже в уме его продифференцировать и получить подынтегральную функцию. 🙂
Особо глазастые студенты при первом взгляде на пример, возможно, узрели вот такую взаимосвязь:
Что ж, респект глазастым! 🙂 Да, действительно, если внести подкоренное выражение 4-х 2 под дифференциал, то пример элементарно сведётся к табличной степенной функции:
Можно так интегрировать? А почему — нет? Математика не запрещает. Но нам ведь размяться с тригонометрической заменой нужно! Вот и изучаем на несложном примере. 🙂
А теперь пример посложнее. Поменяем местами в нашей подынтегральной функции числитель и знаменатель. То есть, просто перевернём подынтегральную функцию. Вот такой пример будем решать:
Пример 2
Давайте, в этот раз используем замену с синусом. Сразу пишем:
И теперь, после подстановки, наш новый интеграл стал выглядеть вот так:
Что делать дальше? Главное — не бояться! И смекалки немного. 🙂
Вообще говоря, на такого рода функции есть свой приём интегрирования (тоже замена, кстати), но мы пока сделаем вид, что про неё не знаем. 🙂 И попробуем выкрутиться с помощью элементарных преобразований, которые мы с вами уже знаем. )
Что здесь можно сделать? Ну, напрашивается подведение под дифференциал, ибо в дроби сидят синус и косинус — родственнички по производной.) Для этого надо попробовать преобразовать подынтегральное выражение так, чтобы везде осталась одна функция — либо синус, либо косинус. Здесь можно всё свести к косинусу. Смотрите, как это делается! По пунктам:
1. Умножаем числитель и знаменатель дроби (вместе с dt!) на sin t. Что именно это даст — узнаем дальше.
2. Заменяем в знаменателе sin 2 t на 1-cos 2 t. Согласно основному тригонометрическому тождеству, ага. 🙂
и подводим косинус под знак дифференциала (про минус тоже не забываем, да).
Вот так. Теперь всё подынтегральное выражение у нас сведено к косинусу. Я согласен, что ещё надо было додуматься домножить всё на sin t, чтобы выйти на такую комбинацию. Но тут уже только богатый опыт рулит. Такое чутьё приходит только с практикой. Так что — решайте примеры! Чем больше, тем лучше.)
Итак, теперь смело заменяем косинус новой буквой. Тэ у нас уже использовано, пусть зэт будет:
Выражаем наш интеграл теперь уже через переменную z:
А теперь в дело вступает наш старый добрый излюбленный приёмчик — отнять/прибавить единичку. 🙂 Продолжаем:
Единичка, я надеюсь, ни у кого проблем в интегрировании не вызывает? А что же касается дроби 1/(z 2 -1), то это не что иное, как табличный интеграл! Открывайте нашу таблицу и ищите похожую формулу. Это седьмая формула, с «высоким» логарифмом:
В роли «а» у нас выступает единичка. Возвращаемся к нашим баранам:
Что ж, заготовка для ответа получена. Теперь поэтапно возвращаемся обратно к иксу:
Вот такой вот интересный пример. И довольно красивый ответ.)
Маньяки могут его продифференцировать. Я продифференцировал. Всё гуд.)
Продолжаем развлекаться. 🙂 Теперь вообще уберём знаменатель и решим вот такой примерчик:
Пример 3
Под интегралом теперь стоит просто чистый корень, безо всего. И тут тоже на помощь придёт тригонометрическая замена.) Давайте, снова будем всё выражать через синус, ибо он удобнее: минус лишний не всплывает, который легко потерять. Действуем:
Как теперь быть с косинусом в квадрате? Если в прошлом примере нам пришлось домножать всё на синус, то тут всё гораздо проще. Призываем на помощь школьную тригонометрию! На сей раз — формулы понижения степени. А чуть конкретнее — вот эту:
И после такого преобразования наш интеграл легко превращается в сумму табличных (ну, или почти табличных :)):
Надеюсь, особо не нужно комментировать, как именно при интегрировании получился синус двух t? Кто не понял — читаем урок « Подведение функции под знак дифференциала ». Там всё популярно изложено. 🙂
Всё. «Рыба» для ответа готова. Осталось правильно перейти к иксу да подставить вместо t в выражения 2t и sin 2t.
Прежде всего, выясним из нашей замены, что же такое это самое t:
Теперь раскроем синус двойного угла: sin2t = 2sin t·cos t
Зачем так сделано? А затем, что теперь и синус и косинус легко выражаются через x (смотрим синюю табличку с нашей заменой)! Вот так:
И теперь наш окончательный ответ полностью готов:
Ну как? Да, я согласен, не самые простые примеры. Так и мы с вами уже всё-таки на приличном уровне, правда?
Что-то мы всё с синусами да косинусами возимся, а тангенс/котангенс как-то обделили вниманием. Давайте и такой примерчик рассмотрим! На десерт.) Он совсем несложный: хватит с вас жести на сегодня! 🙂 Просто чтобы суть замены уловить.)
Пример 4
Не пугаемся внешнего вида примера! Внешность иногда бывает обманчива, да.)
Сразу замечаем под корнем сумму 1+х 2 . Раз сумма, то, стало быть, подходящая замена для ликвидации корня — с тангенсом (или котангенсом). Опять же, по причине нежелания возиться с лишним минусом, я выберу тангенс (а = 1, x = tg t):
И снова перед нами безобидный табличный интеграл! Интегрируем косинус и — готово дело:
Всё. Выражаем теперь нашу первообразную через икс. Как? По формулам тригонометрии, вестимо! У нас есть тангенс, а нас интересует синус.
Так. Квадрат косинуса готов. Осталось лишь из основного тригонометрического тождества вытащить квадрат синуса, извлечь корень и — цель достигнута!
Вот и наш ответ. Довольно простенький на сей раз:
Подытожим наш урок. Давайте разберёмся, зачем в самом начале урока я высказал два обязательных требования, чтобы сам корень был только квадратным (а не кубическим или какой-то более высокой степени), а также чтобы под корнем находилась конструкция вида x 2 ±a 2 . Догадались, почему?
Да потому, что в любой другой ситуации (кубический корень или же под корнем многочлен более высокой степени) у нас просто-напросто не исчезнет иррациональность, и данная замена нам уже никак не поможет свести интеграл к красивому виду. 🙂 И, если вам, вдруг, попался такой пример, то, скорее всего, преобразования более хитрые.
Разумеется, подобные интегралы не ограничиваются этими четырьмя примерами. И для интегралов, содержащих квадратичные иррациональности, есть и более суровые подстановки — Эйлера и Абеля. Но такие подстановки — уже высший пилотаж в интегрировании. Их мы будем изучать ближе к концу раздела. Зато тщательный разбор этих четырёх примеров даст вам возможность уверенно брать хотя бы некоторые интегралы подобного типа. Так что тригонометрическая замена — штука весьма полезная. Мы с ней дружить будем. 🙂 А для дружбы, конечно же, необходимо хорошо знать школьную тригонометрию — основные тождества (их шесть), двойные углы, формулы понижения степени и т.д.
Что ж, на сегодня хватит. А в качестве тренировочного упражнения в этот раз я дам небольшое творческое задание. Чтобы скучно не было.)
Есть в нашей замечательной табличке интегралов парочка довольно страшных формул. Вот эти:
И теперь, в качестве задания, я предлагаю вам доказать эти формулы! С помощью тригонометрической замены, да.) Чтобы вы прочувствовали, откуда что в математике берётся. И берётся явно не с потолка.)
С первой формулой проблем возникнуть не должно: там всё очевидно. А вот со второй («длинным логарифмом») я немного подскажу. В формуле число А для определённости предполагается положительным. Раз оно положительное, то можно совершенно спокойно заменить это самое А на a 2 . И дальше работать уже с заменой через тангенс.) Материала этого (и прошлых) уроков вполне достаточно, чтобы одолеть это задание. Будет вам там парочка сюрпризов! Выручат свойства логарифмов и первообразных (это подсказка! :)).
- Дипломная работа: Применение тригонометрической подстановки для решения алгебраических задач
- Выпускная квалификационная работа
- Е. М. Ковязина
- Литература. 65
- Алгебраическое решение
- Алгебраическое решение
- Возведем обе части уравнения в квадрат
- Итак, исходное уравнение имеет единственный корень
- Алгебраическое решение
- Алгебраическое решение
- Так как выражение от правой части равенства четное и и , выясним вопрос о наличии корней на промежутке . Проверкой устанавливаем, что – корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции и . Так как
- Алгебраическое решение
- .
- Заключение
- Методы решений иррациональных уравнений
- 🎦 Видео
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Дипломная работа: Применение тригонометрической подстановки для решения алгебраических задач
| Название: Применение тригонометрической подстановки для решения алгебраических задач Раздел: Рефераты по математике Тип: дипломная работа Добавлен 21:28:58 27 августа 2010 Похожие работы Просмотров: 416 Комментариев: 11 Оценило: 2 человек Средний балл: 4.5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фамилия | 1 задание | 2 задание | 3 задание | |
| 1 | Бакулин | + |  |  |
| 2 | Бизяев |  |  |  |
| 3 | Вахрушев |  |  |  |
| 4 | Витвицкий | + |  | +д |
| 5 | Громазин | + |  |  к к |
| 6 | Давидюк | + |  |  |
| 7 | Жичкина | + | + | * |
| 8 | Журавлев | + |  |  |
| 9 | Касьянов | + |  | 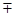 |
| 10 | Колупаева | 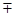 |  | * |
| 11 | Коновалов | 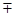 |  | 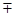 |
| 12 | Коробейников |  | + | +д |
| 13 | Макарова | + |  |  |
| 14 | Новоселов | + |  | * |
| 15 | Овчинников |  |  |  |
| 16 | Прокашев | + |  |  |
| 17 | Сероглазов | 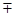 | * | * |
| 18 | Скачилова | + |  |  |
| 19 | Хохлов | 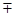 |  | 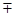 |
| 20 | Черняк | + |  | +д |
| 21 | Шильников | 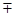 |  | – |
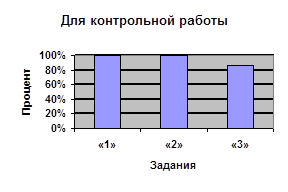
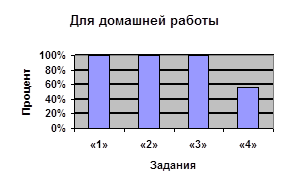
| Процент учащихся, верно выполнивших задание | 57% | 100% | 67% | |
| Процент учащихся, выбравших тригонометрическую подстановку | 100% | 100% | 86% | |
| Процент учащихся, верно решивших с помощью тригонометрической подстановки[2] | 57% | 100% | 67% | |
| Процент учащихся, обосновавших введение тригонометрической подстановки | 100% | 14% | 22% | |
| Процент учащихся, верно решивших другим способом | – | – | 100% | |
Первое задание – решение иррационального уравнения – все учащиеся выполнили с помощью тригонометрической подстановки, причем во всех работах было представлено полное обоснование возможности введения этой подстановки. В восьми работах решение оказалось с ошибками. Все учащиеся, использовавшие подстановку 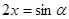
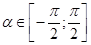
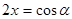
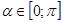
Второе и третье задания были посвящены нахождению наибольшего и наименьшего значений функции.
Второе задание всеми учащимися было решено верно, при этом в качестве метода решения был выбран метод тригонометрической подстановки. Но в отличие от решения первого задания, во втором только двое учащихся дали аргументированное решение с полным обоснованием возможности введения тригонометрической подстановки. В одной работе эта возможность не получила достаточно полного обоснования. Остальные восемнадцать учащихся приступили к решению без доказательства возможности введения замены, причем из них только один верно указал, что 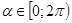
К решению третьего задания приступили двадцать учащихся из двадцати одного. Из них трое решали алгебраическим способом и полностью справились с решением. Один ученик начал решение алгебраическим способом, получил промежуточный результат, который использовал при решении с помощью тригонометрической подстановки, но все решение не было доведено до конца. Шестнадцать учащихся применили метод тригонометрической подстановки для решения, но ни в одной из этих работ не было обоснования введения этой подстановки, и только четверо указали, что 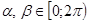
Перейдем к разбору дополнительного задания. Оно содержало уравнение с параметром, для которого требовалось исследовать количество решений в зависимости от параметра. Из двадцати одного ученика к заданию на дополнительную оценку приступили двадцать человек, из них половина верно справилась с ним. Семеро из верно решивших учащихся опирались на графическую иллюстрацию, трое – использовали алгебраический подход. Из не решивших десяти человек семеро привели исходное уравнение с помощью тригонометрической подстановки к виду 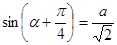
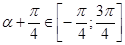
Этап 3. Проведение диагностирующей домашней контрольной работы.
Домашняя контрольная работа была проведена после завершающего четвертого занятия перед написанием итоговой контрольной работы.
1. Решите уравнение 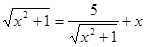
2. Решите уравнение 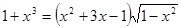
3. Решите уравнение 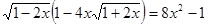
4. Найдите наибольшее и наименьшее значения выражения 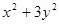
| Фамилия | 1 задание | 2 задание | 3 задание | 4 задание | |
| 1 | Бакулин | +д | + | + |  |
| 2 | Бизяев | +д | + |  |  |
| 3 | Витвицкий | + | +к | + | + |
| 4 | Громазин | + | + | + | – |
| 5 | Давидюк | + | + | + | * |
| 6 | Жичкина | –с | + | + | – |
| 7 | Журавлев | + | + | + | * |
| 8 | Коновалов | + | + | + | + |
| 9 | Коробейников | +с | + | + |  |
| 10 | Макарова | + | + | + |  |
| 11 | Новоселов | + | + | – | * |
| 12 | Овчинников | + | + |  | + |
| 13 | Прокашев | + | + | + | + |
| 14 | Сероглазов | +д | + | + | * |
| 15 | Скачилова | + | + | + |  |
| 16 | Хохлов | +д | + | + | + |
| 17 | Черняк | +с | + | + |  |
| 18 | Шильников | + | + | + | * |
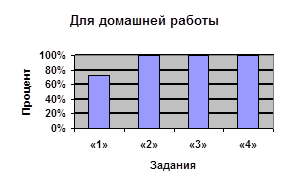
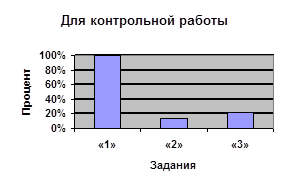
| Процент учащихся, верно выполнивших задание | 94% | 100% | 83% | 89% | |
| Процент учащихся, выбравших тригонометрическую подстановку | 72% | 100% | 100% | 100% | |
| Процент учащихся, верно решивших с помощью тригонометрической подстановки | 92% | 100% | 83% | 89% | |
| Процент учащихся, обосновавших введение тригонометрической подстановки | 100% | 100% | 100% | 56% | |
| Процент учащихся, верно решивших другим способом | 87,5% | – | – | – | |
| Процент учащихся, решавших двумя способами | 17% | 0% | 0% | 0% | |
Первые три задания были посвящены решению иррациональных уравнений. Причем решить первое уравнение было рекомендовано двумя способами: с помощью тригонометрической подстановки и без нее. Это было сделано с той целью, чтобы показать учащимся: не всегда введение тригонометрической подстановки упрощает решение. Иногда применение стандартного метода для решения задач оказывается более эффективным. Таким образом, уравнение было призвано обратить внимание учащихся не необходимость обдуманного введения тригонометрической подстановки. Пример не вызвал серьезных затруднений, из восемнадцати работ только в одной были ошибки. Как правило, для решения учащиеся выбирали и обосновывали подстановку
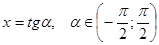
Одним учащимся был предложен другой вариант тригонометрической подстановки
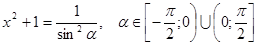
но само решение оказалось более громоздким.
Со вторым заданием справились все учащиеся.
В третьем задании ошибки возникли у трех учащихся из восемнадцати и были связаны с неверным отбором корней.
Вновь наибольшие затруднения вызвало задание на нахождение наибольшего и наименьшего значений выражения. Даже среди тех, кто получил верный ответ, немногие обосновали введение тригонометрической подстановки.
Этап 4. Анализ полученных результатов опытной работы.
Результаты контрольной и домашней контрольной работ можно представить в виде диаграмм.
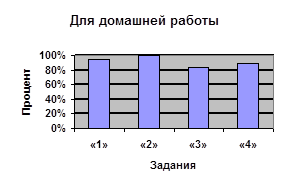
Процент учащихся, выбравших тригонометрическую подстановку
В основном в качестве метода решения предложенных алгебраических задач учащиеся выбирали метод тригонометрической подстановки. Другим способом решали, если задание состояло в том, чтобы найти наибольшее значение выражения при заданных в системе условиях (как в контрольной работе) или если было рекомендовано решать другим способом (как в домашней контрольной работе).
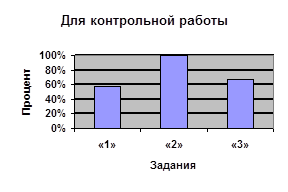
Процент учащихся, верно справившихся с заданиями
Из диаграмм видно, что наибольшие затруднения вызывали у учащихся задания двух типов. Во – первых, задания на нахождение наибольшего и наименьшего значений выражения. Во – вторых, иррациональные уравнения, область допустимых значений которых можно представить неравенством 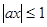
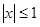
Процент учащихся, обосновавших введение тригонометрической подстановки
Во всех заданиях, где учащимся было предложено решить иррациональное уравнение, тригонометрическая подстановка была обоснована. Хуже обстояло дело с обоснованием введения тригонометрической подстановки, если речь шла о двух переменных. В этом случае учащиеся, как правило, приступали к решению, доводили его до верного ответа, но не обосновывали законность произведенной замены.
Так как только в двух случаях (в одном задании из контрольной и в одном задании из домашней контрольной работы) учащиеся предложили другое решение без использования тригонометрической подстановки
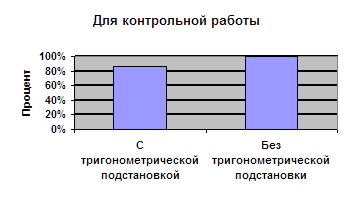
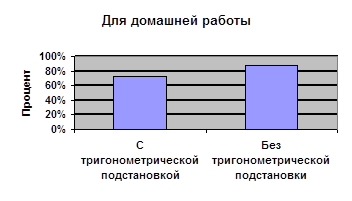
Сравним процент учащихся, решивших верно с помощью тригонометрической подстановки и без нее
Решение более привычным и отработанным способом для учащихся оказалось эффективнее, чем с помощью введения тригонометрической подстановки. И это не удивительно. Тема «Применение тригонометрической подстановки для решения алгебраических задач» является довольно сложной, речь идет о ее рассмотрении на факультативных занятиях только в классах с углубленным изучением математики. Пять факультативных занятий для того чтобы учащиеся овладели этим методом, безусловно, мало, о чем свидетельствуют результаты. Но ввиду того, что применение тригонометрической подстановки может оказать существенную помощь в решении некоторых классов задач (например, иррациональных уравнений, задач на нахождение наибольшего и наименьшего значений функции и других), желательно продолжить работу с учащимися над овладением этим методом и вернуться к нему в конце 11 класса. В пользу этого говорит еще и тот факт, что при решении предложенных задач учащиеся выбирали именно этот способ решения для получения ответа. Особенно удачно учащиеся использовали замену при решении иррациональных уравнений, видели возможность введения тригонометрической подстановки и обосновывали это введение. Сама замена стала интересной для учащихся не только тем, что позволила решить непростые конкурсные примеры, но и указала на связь между алгеброй и тригонометрией, показала, что введение тригонометрической подстановки не только не усложняет решение, а в некоторых случаях существенно упрощает его, тем самым повышая значимость самой тригонометрии в глазах учащихся.
Видео:Система иррациональных уравнений #1Скачать

Заключение
При проведении исследования были поставлены и решены следующие задачи:
1. Исследованы теоретические основы возможности введения тригонометрической подстановки.
2. Проведена работа по подбору и объединению в одном источнике решений с помощью тригонометрической подстановки разнообразных алгебраических заданий: уравнений, неравенств, их систем, задач с параметрами и задач на отыскание наибольшего и наименьшего значений функции. Работа включает в себя задания, решение которых с помощью тригонометрической подстановки и без нее равноценны, задания, которые не могут быть решены стандартными алгебраическими приемами без применения тригонометрической подстановки и задания, которые решаются без тригонометрической подстановки проще.
3. Проведен сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее. Метод тригонометрической подстановки рассмотрен во многих источниках по математике, в том числе [3]-[6], [9]-[14], [16], [18], [22]-[25], [29]-[32], [37]-[39], [42]-[45], [47], [49], [51], [57]. Но практически ни в одном из них не был проведен сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее и практически нет источников, в которых была бы представлена возможность применения тригонометрической подстановки для решения большого класса задач.
4. На основе проведенного сравнительного анализа была разработана методика изучения тригонометрической подстановки при решении алгебраических задач на факультативных занятиях по математике в старших классах с углубленным изучением математики.
5. Проведено опытное испытание эффективности разработанной методики в 10 классе ФМЛ.
Опытная работа показала, что введение факультативного курса «Применение тригонометрической подстановки для решения алгебраических задач» в классы с углубленным изучением математики оправдано. В состав диагностирующей контрольной работы, которая была проведена на завершающем занятии факультативного курса, были включены задачи, которые допускали как алгебраический способ решения, так и решение с помощью тригонометрической подстановки. Школьникам была предоставлена свобода выбора метода решения каждого задания. Результаты работы показали, что учащиеся без особого труда выделяют задачи, в которых возможно ввести тригонометрическую подстановку; применяют ее для решения трудных и очень трудных конкурсных задач; осуществляют сравнение и выбор наиболее рационального способа решения. А значит, гипотеза, сделанная в начале дипломной работы, подтвердилась. Введение материала, связанного с тригонометрической подстановкой, на факультативных занятиях в классах с углубленным изучением математики способствует развитию творческих способностей учащихся и подготавливает их к вступительным экзаменам в вузы с повышенными требованиями к математике. Единственное, над чем еще можно поработать – грамотное обоснование введенной замены.
1. Алгебра и математический анализ. 10 класс: Учебное пособие для школ и классов с углубленным изучением математики / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. – М.: Мнемозина, 2001. – С. 335.
2. Алгебра и математический анализ. 11 класс: Учебное пособие для школ и классов с углубленным изучением математики / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. – М.: Мнемозина, 2001. – С. 288.
3. Алексеев А. Тригонометрические подстановки / А. Алексеев, Л. Курляндчик // Квант. – №2. – 1995. – С. 40–42.
4. Балаян Э. Н. Репетитор по математике для поступающих в вузы / Э. Н. Балаян. – Ростов–на–Дону: Изд-во Феникс, 2003. – С. 736.
5. Болтянский В. Г. Лекции и задачи по элементарной математике / В. Г. Болтянский, Ю. В. Сидоров, М. И. Шабунин. – М.: Изд-во Наука, 1972. – С. 592.
6. Вавилов В. В. Задачи по математике. Алгебра / В. В. Вавилов, И. И. Мельников, С. Н. Олехник, П. И. Пасиченко. – М.: Наука, 1988. – С. 439.
7. Василевский А. Б. Методы решения задач / А. Б. Василевский. – Минск: Вышэйшая школа, 1974. – С. 240.
8. Василевский А. Б. Обучение решению задач: Учебное пособие для педагогических институтов / А. Б. Василевский. – Минск: Вышэйшая школа, 1988. – С. 255.
9. Вороной А. Н. Пять способов доказательства одного неравенства / А. Н. Вороной // Математика в школе. – №4. – 2000. – С. 12.
10. Вороной А. Н. Циклические системы уравнений / А. Н. Вороной // Математика в школе. – №7. – 2003. – С. 71-77.
11. Всероссийские математические олимпиады школьников: Книга для учащихся / Г. Н. Яковлев, Л. П. Купцов, С. В. Резниченко, П. Б. Гусятников. – М.: Просвещение, 1992. – С. 383.
12. Горнштейн П. И. Экзамен по математике и его подводные рифы / П. И. Горнштейн, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М.: Илекса, 2004. – С. 236.
13. Горнштейн П. И. Задачи с параметрами / П. И. Горнштейн, В. Б. Полонский, М. С. Якир. – М.: Илекса, Харьков: Гимназия, 2002. – С. 336.
14. Горнштейн П. И. Тригонометрия помогает алгебре / П. И. Горнштейн. – М.: Бюро Квантум, 1995. – С. 100-103. – Приложение к ж. «Квант», №3/95.
15. Громов А. И. Математика для поступающих в вузы. Методы решения задач по элементарной математике и началам анализа / А. И. Громов, В. М. Савчин. – М.: Изд-во РУДН Народная Компания Евразийский регион, 1997. – С. 264.
16. Дорофеев Г. В. Пособие по математике для поступающих в вузы. Избранные вопросы элементарной математики / Г. В. Дорофеев, М. К. Потапов, Н. Х. Розов. – М.: Просвещение, 1976. – С. 640.
17. Епифанова Т. Н. Отыскание экстремальных значений функций различными способами / Т. Н. Епифанова // Математика в школе. – №4. – 2000. – С. 52-55.
18. Зарубежные математические олимпиады / С. В. Конягин, Г. А. Тоноян, И. Ф. Шарыгин. – М.: Наука, 1987. – С. 416.
19. Канин Е. С. Учебные математические задачи: Учебное пособие / Е. С. Канин. – Киров: Изд-во ВятскогоГГУ, 2003. – С. 191.
20. Колягин Ю. М. Задачи в обучении математике / Ю. М. Колягин. – М.: Просвещение, 1977. – С. 143.
21. Лапушкина Л. И. Системы алгебраических уравнений / Л. И. Лапушкина, М. И. Шабунин // Математика в школе. – №6. – 1998. – С. 22-26.
22. Махров В. Г. Новый репетитор по математике для старшеклассников и абитуриентов / В. Г. Махров, В. Н. Махрова. – Ростов–на–Дону: Изд-во Феникс, 2004. – С. 544.
23. Мельников И. И. Как решать задачи по математике на вступительных экзаменах / И. И. Мельников, И. Н. Сергеев. – М.: Изд-во Московского университета, 1990. – С. 303.
24. Мерзляк А. Г. Тригонометрия: Задачник по школьному курсу. 8-11 класс / А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович. – М.: АСТ – ПРЕСС: Магистр, 1998. – С. 655.
25. Мерзляк А. Г. Неожиданный шаг или сто тринадцать красивых задач / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – Киев: Агрофирма Александрия, 1993. – С. 59.
26. Методика преподавания математики в средней школе: Общая методика. Учебное пособие для студентов пед. ин-тов по спец. 2104 «Математика» и 2105 «Физика» / Сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – С. 336.
27. Методика преподавания математики в средней школе: Частная методика: Учебное пособие для студентов пед. ин-тов по физ.-мат. Спец. / Сост. В. И. Мишин. – М.: Просвещение, 1987. – С. 414.
28. Мордкович А. Г. Беседы с учителями математики / А. Г. Мордкович. – М.: Школа – Пресс, 1995. – С. 272.
29. Морозова Е. А. Международные математические олимпиады. Задачи, итоги, решения. Пособие для учащихся / Е. А. Морозова. – М.: Просвещение, 1976. – С. 288.
30. Московский государственный университет // Математика в школе. – №10. – 2002. – С. 28-43.
31. Нараленков М. И. Вступительный экзамен по математике. Алгебра: как решать задачи: Учебно-практическое пособие / М. И. Нараленков. – М.: Изд-во Экзамен, 2003. – С. 448.
32. Олехник С. Н. Нестандартные методы решения уравнений и неравенств: Справочник / С. Н. Олехник, М. К. Потапов, П. И. Пасиченко. – М.: Изд-во МГУ, 1991. – С. 143.
33. Петров В. В. Нестандартные задачи / В. В. Петров, Е. В. Елисеева // Математика в школе. – №8. – 2001. – С. 56-59.
34. Писаревский Б. М. Задачи об экстремумах / Б. М. Писаревский // Математика в школе. – №5. – 2004. – С. 47-51.
35. Письменный Д. Т. Математика для старшеклассников / Д. Т. Письменный. – М.: Айрис, Рольф, 1996. – С. 281.
36. Пойа Д. Обучение через задачи / Д. Пойа // Математика в школе. – №3. – 1970. – С. 89-91.
37. Потапов М. К. Готовимся к экзаменам по математике: Учебное пособие для поступающих в вузы и старшеклассников / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. – М.: Научно – технический центр «Университетский»: АСТ – Пресс, 1997. – С. 352.
38. Потапов М. К. Конкурсные задачи по математике / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. – М.: ФИЗМАТЛИТ, 2001. – С. 400.
39. Потапов М. К. Математика. Методы решения задач. Для поступающих в вузы: Учебное пособие / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. – М.: Дрофа, 1995. – С. 336.
40. Потапов, М. К. Рассуждения с числовыми значениями при решении систем уравнений / М. К. Потапов, А. В. Шевкин // Математика в школе. – №3. – 2005. – С. 24-29.
41. Программы для общеобразоват. Школ, гимназиев, лицеев: Математика. 5-11 класс / Сост. Г. М. Кузнецова, Н. Г. Миндюк. – М.: Дрофа, 2002.– С. 320.
42. Саакян С. М. Задачи по алгебре и началам анализа для 10-11 классов / С. М. Саакян, Гольдман А. М., Денисов Д. В. – М.: Просвещение, 1990. – С. 256.
43. Смоляков А. Н. Тригонометрические подстановки в уравнения и неравенства / А. Н. Смоляков // Математика в школе. – №1. – 1996. – С.4.
44. Супрун В. П. Избранные задачи повышенной сложности по математике / В. П. Супрун. – Минск: Полымя, 1998. – С. 108.
45. Терешин Н. А. 2000 задач по алгебре и началам анализа. 10 класс / Н. А. Терешин, Т. Н. Терешина. – М.: Аквариум, 1998. – С. 256.
46. Ткачук В. В. Математика – абитуриенту: Все о вступительных экзаменах в вузы. Том 1 / В. В. Ткачук. – М.: ТЕИС, 1996. – С. 415.
47. Ткачук В. В. Математика – абитуриенту: Все о вступительных экзаменах в вузы. Том 2 / В. В. Ткачук. – М.: ТЕИС, 1996. – С. 414.
48. Фарков А. В. Математические олимпиады в школе. 5-11 класс / А. В. Фарков. – М.: Айрис-пресс, 2002. – С. 160.
49. Фирстова Н. И. Метод замены переменной при решении алгебраических уравнений / Н. И. Фирстова // Математика в школе. – №5. – 2002. – С. 68-71.
50. Фридман Л. И. Как научиться решать задачи / Л. И. Фридман, Е. Н. Турецкий. – М.: Московский психолого-социальный институт, 1999. – С. 240.
51. Черкасов О. Ю. Математика: Методические указания для поступающих в вузы / О. Ю. Черкасов, А. Г. Якушев. – М.: УНЦ ДО МГУ, 1996. – С. 368.
52. Черкасов О. Ю. Математика: Скорая помощь абитуриентам / О. Ю. Черкасов, А. Г. Якушев. – М.: Учебный центр Московский лицей, 1995. – С. 348.
53. Шабунин М. И. Математика для поступающих в вузы. Неравенства и системы неравенств / М. И. Шабунин. – М.: Аквариум, 1997. – С. 256.
54. Шабунин М. И. Математика для поступающих в вузы. Уравнения и системы уравнений / М. И. Шабунин. – М.: Аквариум, 1997. – С. 272.
55. Шарыгин И. Ф. Математика для поступающих в вузы: Учебное пособие / И. Ф. Шарыгин. – М.: Дрофа, 2000. – С. 416.
56. Шарыгин И. Ф. Математика для школьников старших классов / И. Ф. Шарыгин. – М.: Дрофа, 1995. – С. 486.
57. Шарыгин И. Ф. Решение задач: Учебное пособие для 10 класса общеобразовательных учреждений / И. Ф. Шарыгин. – М.: Просвещение, 1994. – С. 350.
Тема: применение тригонометрической подстановки для решения иррациональных уравнений.
1. Вспомнить теоретические основы введения тригонометрической подстановки.
2. Рассмотреть применение тригонометрической подстановки для решения иррациональных уравнений в случае, когда множество значений переменной 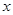
3. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее.
1. Решить уравнение 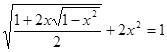
2. Решите уравнение 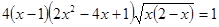
3. Решить уравнение 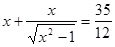
4. Решить уравнение 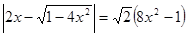
1. Решить уравнение 
2. Решить уравнение 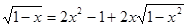
3. Решить уравнение 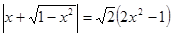
Литература: [3], [4], [12], [14], [23] – [25], [31], [32], [37] – [39], [43], [44], [47] – [51], [57].
Тема: применение тригонометрической подстановки для решения систем уравнений.
1. Рассмотреть применение тригонометрической подстановки для решения сложных, олимпиадных систем.
2. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее, где это возможно.
3. Привести пример системы, решить которую без тригонометрической подстановки не возможно.
1. Решить систему уравнений 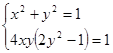
2. Решить систему 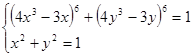
3. Выяснить, сколько решений имеет система уравнений 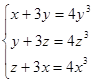
4. При каких значениях параметра система имеет решение 
1. Решить систему 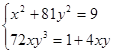
2. Решить систему 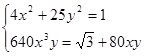
3. Сколько решений имеет система уравнений 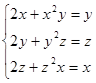
Литература: [3], [6] – [8], [10], [12], [14], [18], [24], [30], [43].
Тема: применение тригонометрической подстановки для решения задач на отыскание наибольшего и наименьшего значений функции.
1. Вспомнить основные методы решения задач на отыскание наибольшего и наименьшего значений функции.
2. Показать, как метод тригонометрической подстановки применяется для решения задач на нахождение наибольшего и наименьшего значений функции.
3. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее.
1. Найти наибольшее и наименьшее значение выражения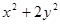
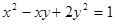
2. Найти наибольшее и наименьшее значение выражения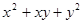
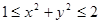
3. Среди всех решений системы найдите такие, при которых выражение 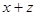
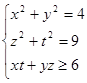
4. Выяснить, при каких значениях параметра неравенство имеет решения 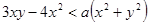
1. Найти наибольшее и наименьшее значение выражения 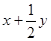
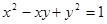
2. Найти наибольшее и наименьшее значение выражения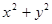
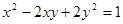
3. Среди всех решений системы найти такие, при каждом из которых выражение 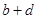
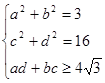
Литература: [4], [14], [22], [24], [31], [42].
[1] Пример 2 пункта 1.2 Рациональные уравнения
[2] Здесь и далее процент подсчитывается от количества учащихся, выбравших указанный способ решения
Видео:Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

Методы решений иррациональных уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
1 способ. Введение новой переменной
Метод замены переменной или метод подстановки очень часто используется при решении иррациональных уравнений и неравенств. Он позволяет значительно упростить решение, разбить его на самостоятельные этапы. Решить уравнение. 
Выполняем обратную подстановку
Ответ: -5; 2.
2 способ. Исследование ОДЗ.
Решить уравнение.
Решение. Замечаем, что ОДЗ уравнения состоит из одной точки х= 1 . Проверкой убеждаемся, что х= 1 – решение уравнения .
3 способ. Умножение обеих частей уравнения на сопряженный множитель.
Решить уравнение
Решение. Умножим обе части уравнения на 
Получим, 
Имеем,
Отсюда,
Проверкой убеждаемся, что х = 1 является корнем данного уравнения.
4 способ. Сведение уравнения к системе рациональных уравнений с помощью введения переменной.
Решить уравнение
Решение. Положим 
5 способ. Выделение полного квадрата
Решить уравнение
Решение. Заметим, что



Следовательно, имеем уравнение
Данное уравнение равносильно совокупности двух систем:

Решением первой системы будет х =0, решением второй системы – все числа, удовлетворяющие неравенству
6 способ. Использование ограниченности выражений, входящих в уравнение
Решить уравнение
Так как 




Решая второе уравнение системы, найдем х=0 . Это значение удовлетворяет и первому уравнению системы. Итак, х= 0 – корень уравнения.
7 способ: Использование свойств монотонности функций.
Решить уравнение 

🎦 Видео
Иррациональные уравнения и их системы. 11 класс.Скачать

Решение иррационального уравнения с помощью тригонометрической заменыСкачать

7.12 Тригонометрическая подстановка в интегралах ∫ R(sinx, cosx)dxСкачать

7.5 Интегралы от тригонометрических функций / интеграл от синуса и косинуса в степениСкачать

7.10 Универсальная тригонометрическая подстановка / формулы с выводом / примерыСкачать

Тригонометрическая замена в иррациональном уравнении. Задание 13 ЕГЭ по математике. (51)Скачать

Система тригонометрических уравнений. Или иррациональных?Скачать

Иррациональное уравнение на 2 минутыСкачать

Неопределенный интеграл от иррациональной функции: 2 способа решения.Скачать

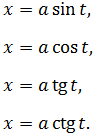
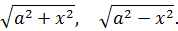
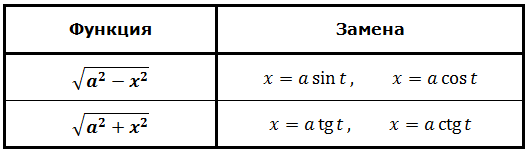
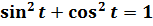
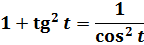
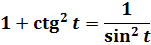
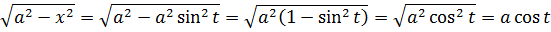
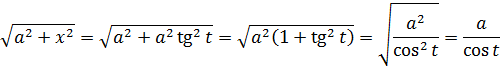
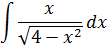
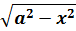
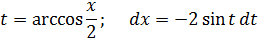
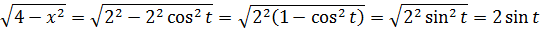
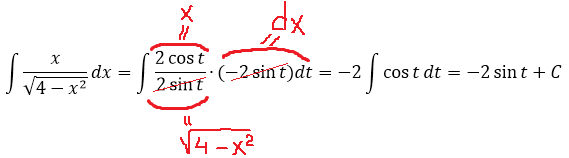
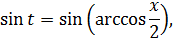
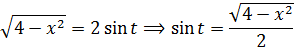
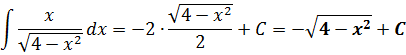
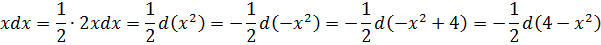
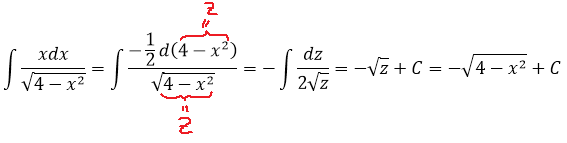
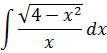
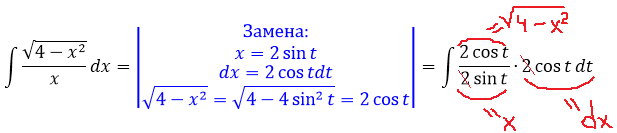
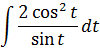
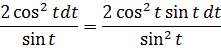
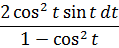
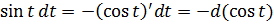
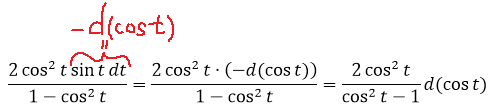
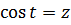
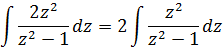
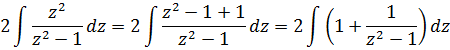
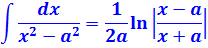
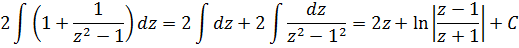
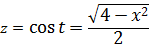
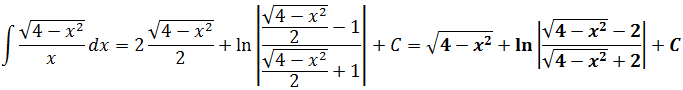
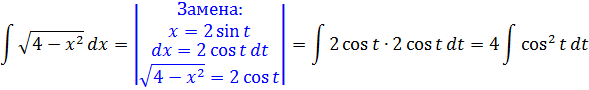
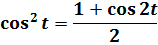
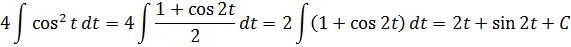
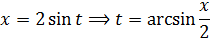
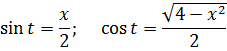
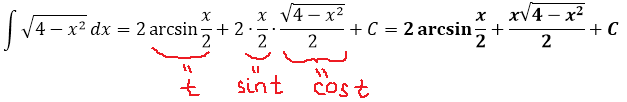
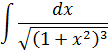
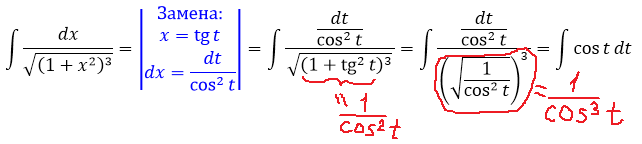
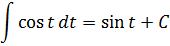
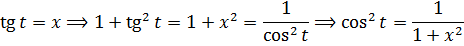
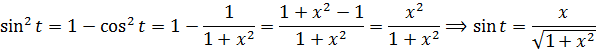
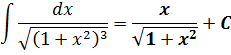
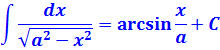
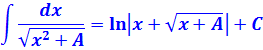

 удалось преобразовать к виду
удалось преобразовать к виду  , то нужно ввести новую переменную
, то нужно ввести новую переменную 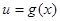 , решить уравнение
, решить уравнение 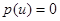 , а затем рассмотреть совокупность уравнений
, а затем рассмотреть совокупность уравнений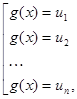
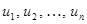 – корни уравнения
– корни уравнения 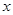 из рассматриваемой области соответствует хотя бы одно значение
из рассматриваемой области соответствует хотя бы одно значение 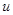 , удовлетворяющее равенству
, удовлетворяющее равенству 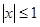 , то удобны замены
, то удобны замены 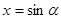 или
или 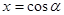 . В первом случае достаточно рассмотреть
. В первом случае достаточно рассмотреть 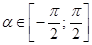 , так как на этом промежутке непрерывная функция
, так как на этом промежутке непрерывная функция 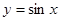 возрастает, поэтому каждое свое значение принимает ровно в одной точке. Непрерывная функция
возрастает, поэтому каждое свое значение принимает ровно в одной точке. Непрерывная функция 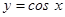 убывает на промежутке
убывает на промежутке 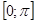 , поэтому также каждое свое значение принимает ровно в одной точке. Вот почему в случае замены
, поэтому также каждое свое значение принимает ровно в одной точке. Вот почему в случае замены 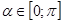 . Причем какую из двух подстановок выбрать, зависит от конкретной ситуации.
. Причем какую из двух подстановок выбрать, зависит от конкретной ситуации.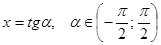 или
или 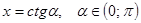 , так как область значения функции
, так как область значения функции 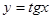 и
и 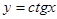 на соответствующих промежутках есть множество всех действительных чисел.
на соответствующих промежутках есть множество всех действительных чисел.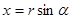 или
или 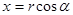 , где
, где 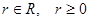 , а выбор значений
, а выбор значений 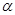 снова зависит от конкретной ситуации.
снова зависит от конкретной ситуации.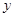 , целесообразно положить
, целесообразно положить 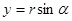 , где
, где 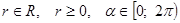 . Такая замена законна. Действительно, для любых
. Такая замена законна. Действительно, для любых 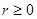 , что
, что 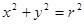 . При
. При 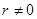 имеем
имеем 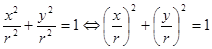 . А числа, сумма квадратов которых равна единице, по модулю не превосходят единицы и их можно рассматривать как синус и косинус некоторого угла. Геометрический смысл такой замены состоит в следующем: для каждой точки
. А числа, сумма квадратов которых равна единице, по модулю не превосходят единицы и их можно рассматривать как синус и косинус некоторого угла. Геометрический смысл такой замены состоит в следующем: для каждой точки 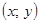 определяется расстояние
определяется расстояние 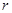 до начала координат и угол
до начала координат и угол 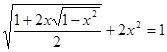 [12].
[12].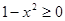 , то
, то 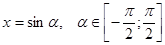 . Уравнение примет вид
. Уравнение примет вид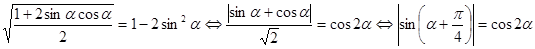 .
.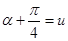 , где
, где 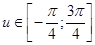 , тогда
, тогда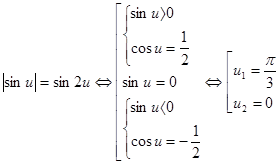 .
.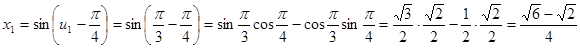 .
.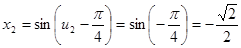 .
.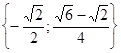 .
.
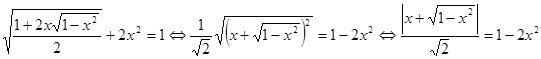 .
.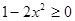 , то
, то 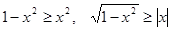 . Значит,
. Значит, 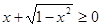 , поэтому можно раскрыть модуль
, поэтому можно раскрыть модуль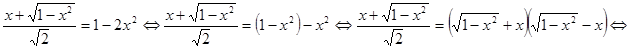
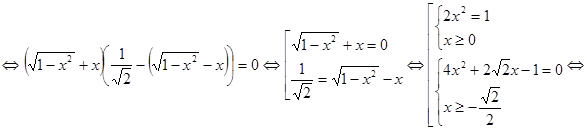
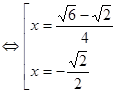 .
.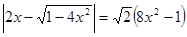 [14].
[14].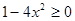 , что равносильно условию
, что равносильно условию 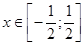 , тогда
, тогда 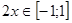 . Поэтому можно положить
. Поэтому можно положить 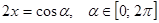 . Уравнение примет вид
. Уравнение примет вид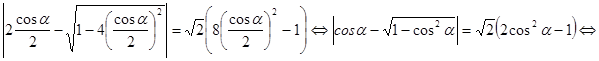
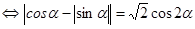 .
.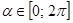 , то
, то 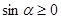 . Раскроем внутренний модуль
. Раскроем внутренний модуль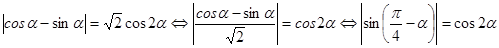 .
.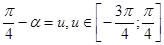 , тогда
, тогда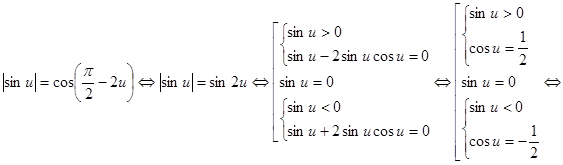
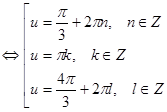 .
.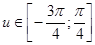 удовлетворяют два значения
удовлетворяют два значения 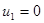 и
и 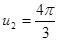 .
.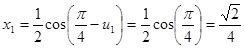 .
.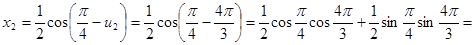
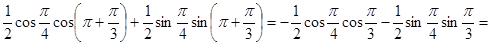
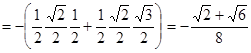 .
.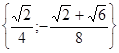 .
.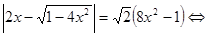
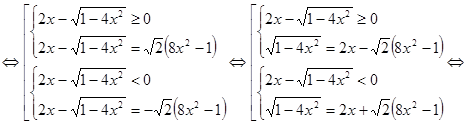
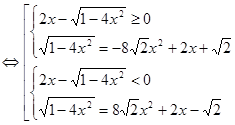 .
.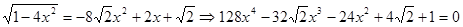 .
.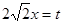 , тогда
, тогда 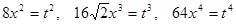 . Уравнение перепишется в виде
. Уравнение перепишется в виде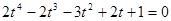 .
.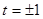 – корень, тогда делением многочлена
– корень, тогда делением многочлена 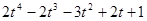 на двучлен
на двучлен 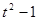 получаем разложение правой части уравнения на множители
получаем разложение правой части уравнения на множители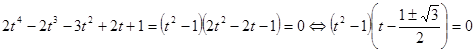 .
.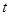 перейдем к переменной
перейдем к переменной 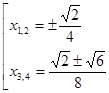 .
.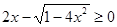 удовлетворяют два значения
удовлетворяют два значения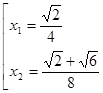 .
.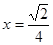 – корень.
– корень.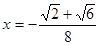 тоже корень.
тоже корень.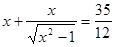 [31].
[31].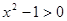 , то
, то 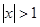 . Заметим, что отрицательное значение неизвестного не может быть решением задачи. Действительно, преобразуем исходное уравнение к виду
. Заметим, что отрицательное значение неизвестного не может быть решением задачи. Действительно, преобразуем исходное уравнение к виду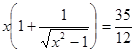 .
.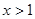 , тогда
, тогда 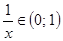 , поэтому можно положить
, поэтому можно положить 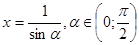 Исходное уравнение перепишется в виде
Исходное уравнение перепишется в виде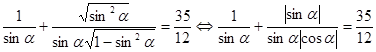 .
.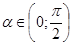 , то
, то 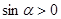 и
и 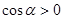 . Уравнение примет вид
. Уравнение примет вид .
.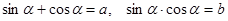 . Перейдем от уравнения к равносильной системе
. Перейдем от уравнения к равносильной системе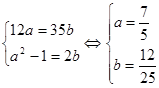 .
.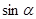 и
и 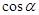 являются корнями квадратного уравнения
являются корнями квадратного уравнения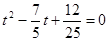 .
.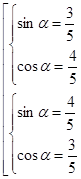 .
.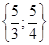 .
.
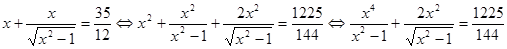 .
.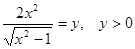 , тогда уравнение запишется в виде
, тогда уравнение запишется в виде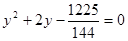
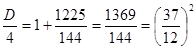
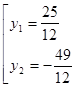 .
.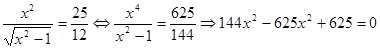
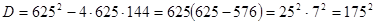
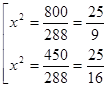 .
.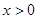 , то
, то 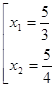 .
.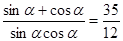 , которое сводится введением замены к системе уравнений. В определенном смысле эту замену тоже можно считать нестандартной, а знакомство с ней позволяет обогатить арсенал приемов и методов решения тригонометрических уравнений.
, которое сводится введением замены к системе уравнений. В определенном смысле эту замену тоже можно считать нестандартной, а знакомство с ней позволяет обогатить арсенал приемов и методов решения тригонометрических уравнений.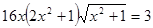 [4].
[4].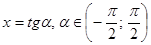 . Тогда
. Тогда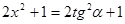 ,
,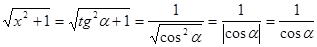 ,так как
,так как 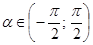 .
.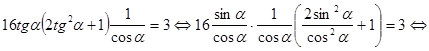
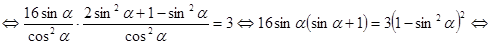
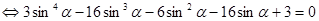 .
.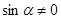 , поделим обе части уравнения на
, поделим обе части уравнения на 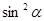 , получим
, получим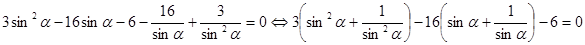 .
.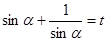 , тогда
, тогда 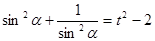 . Уравнение примет вид
. Уравнение примет вид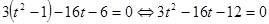 .
.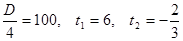 .
.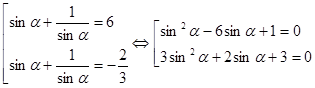 .
.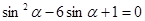 .
.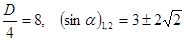 .
.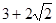 не может быть значением синуса, так как
не может быть значением синуса, так как 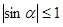 для любых значений аргумента.
для любых значений аргумента.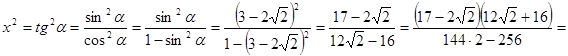
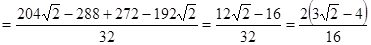 .
.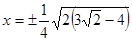 .
.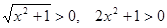 и правая часть исходного уравнения положительна, то
и правая часть исходного уравнения положительна, то 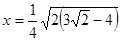 .
.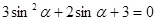 .
.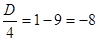 .
.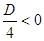 .
.
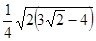 .
.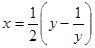 , предложенную И. Ф. Шарыгиным [57].
, предложенную И. Ф. Шарыгиным [57].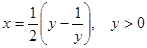 , тогда
, тогда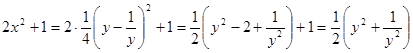
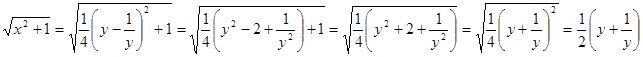 Преобразуем правую часть уравнения
Преобразуем правую часть уравнения 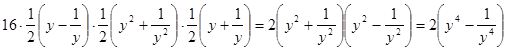 .
.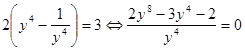 .
.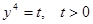 , тогда
, тогда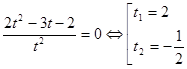 .
.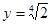 , а
, а 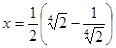 .
.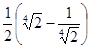 .
.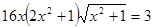 , то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени
, то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени 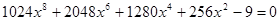 , найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения
, найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения 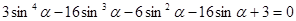 , если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой
, если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой 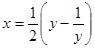 технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.
технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.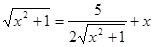 [51].
[51].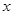 может принимать любые действительные значения, можно положить
может принимать любые действительные значения, можно положить 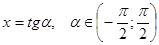 . Уравнение примет вид
. Уравнение примет вид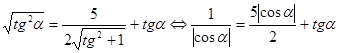 .
.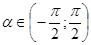 , можно раскрыть модуль
, можно раскрыть модуль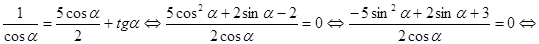
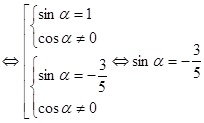 .
.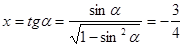 .
.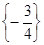 .
.
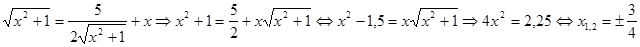 Проверкой убеждаемся, что
Проверкой убеждаемся, что 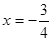 – корень.
– корень.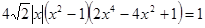 [37].
[37].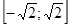 . Действительно, если
. Действительно, если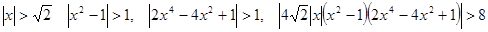 .
.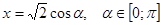 . Тогда каждому корню
. Тогда каждому корню 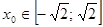 исходного уравнения будет соответствовать ровно один корень
исходного уравнения будет соответствовать ровно один корень 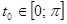 , где
, где 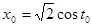 . Наоборот, каждому корню
. Наоборот, каждому корню 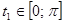 уравнения соответствует ровно один корень исходного уравнения. Таким образом, задача может быть переформулирована так: сколько корней на промежутке
уравнения соответствует ровно один корень исходного уравнения. Таким образом, задача может быть переформулирована так: сколько корней на промежутке 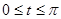 имеет уравнение
имеет уравнение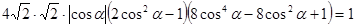 .
.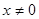 и
и 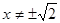 , то можно взять
, то можно взять 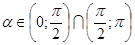 . Заметим, что если
. Заметим, что если 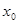 — корень данного уравнения, то и
— корень данного уравнения, то и 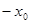 тоже корень. Вот почему достаточно рассмотреть
тоже корень. Вот почему достаточно рассмотреть 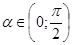 , то есть отыскать только положительные решения. С учетом выше изложенного исходное уравнение перепишется в виде
, то есть отыскать только положительные решения. С учетом выше изложенного исходное уравнение перепишется в виде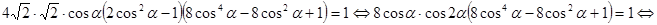
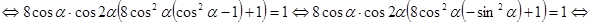
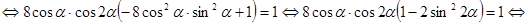
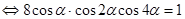 .
.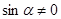 , получим
, получим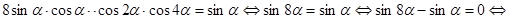
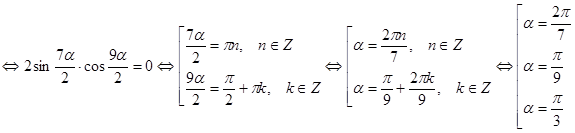 .
.

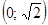 . Проверкой устанавливаем, что
. Проверкой устанавливаем, что 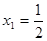 – корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции
– корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции 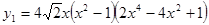 и
и 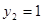 . Так как
. Так как
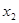 и
и 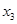 , что
, что 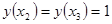 . Поэтому на промежутке
. Поэтому на промежутке 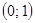 уравнение имеет три корня, а на всей числовой прямой – шесть корней.
уравнение имеет три корня, а на всей числовой прямой – шесть корней.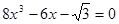 .
.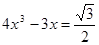 .
.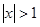 , тогда
, тогда 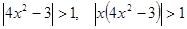 . Получили, что при
. Получили, что при 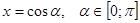 . Уравнение примет вид
. Уравнение примет вид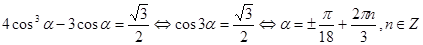 .
.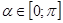 удовлетворяют три значения
удовлетворяют три значения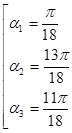 .
.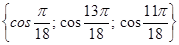 .
.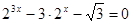 .
.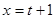 , тогда уравнение перепишется в виде
, тогда уравнение перепишется в виде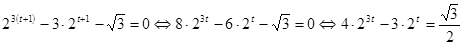 .
.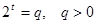 , получим
, получим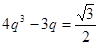 .
.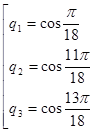 .
.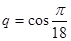 . Перейдем к переменной
. Перейдем к переменной 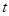 , а затем к переменной
, а затем к переменной 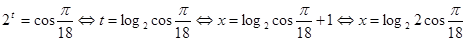 .
.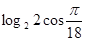 .
.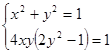 [3].
[3].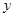 равен единице, то каждое из этих чисел по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Поэтому можно положить
равен единице, то каждое из этих чисел по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Поэтому можно положить 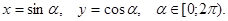 Второе уравнение системы примет вид
Второе уравнение системы примет вид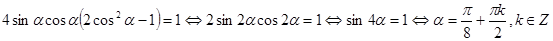 .
.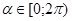 удовлетворяют четыре значения
удовлетворяют четыре значения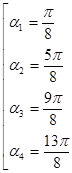 .
.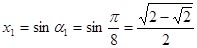
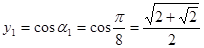 .
.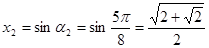
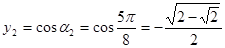 .
.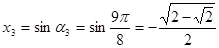
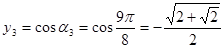 .
.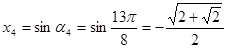
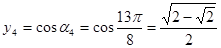 .
.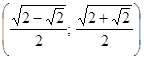 ;
; 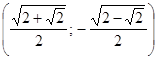 ;
; 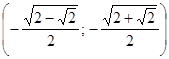 ;
; 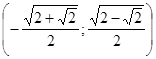 .
.
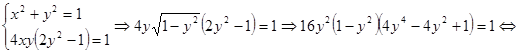
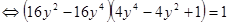 .
.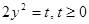 , тогда
, тогда 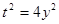 . Имеем
. Имеем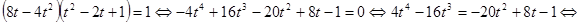
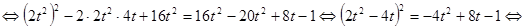
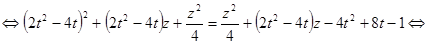
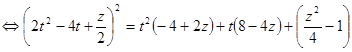 .
.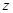 так, чтобы многочлен, стоящий в правой части равенства, стал полным квадратом. Для этого он должен иметь один двукратный корень, то есть
так, чтобы многочлен, стоящий в правой части равенства, стал полным квадратом. Для этого он должен иметь один двукратный корень, то есть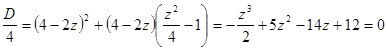 .
.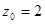 является корнем уравнения
является корнем уравнения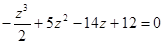 .
.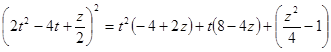 , после чего оно примет вид
, после чего оно примет вид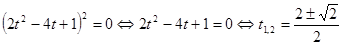 .
.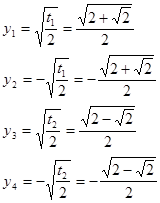
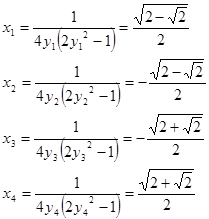
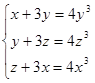 [18].
[18]. . Попытки доказать, что система не имеет других решений, положительных результатов не дают. Неоценимую помощь в решении такого класса задач оказывает метод тригонометрической подстановки.
. Попытки доказать, что система не имеет других решений, положительных результатов не дают. Неоценимую помощь в решении такого класса задач оказывает метод тригонометрической подстановки.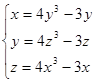 .
. по абсолютной величине не превосходят единицы. Пусть
по абсолютной величине не превосходят единицы. Пусть  , то
, то 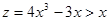 . Пришли к противоречию. Если число
. Пришли к противоречию. Если число  , то
, то  . Опять пришли к противоречию. Итак
. Опять пришли к противоречию. Итак  .
. ,
,  ,
, 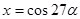 . Число решений исходной системы равно числу решений уравнения
. Число решений исходной системы равно числу решений уравнения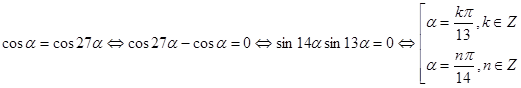 .
.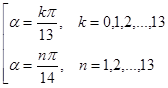 .
.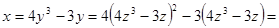
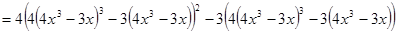 .
.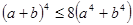 [43].
[43].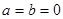 неравенство верное.
неравенство верное.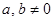 найдется угол
найдется угол 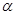 , что
, что 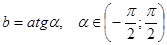 . Исходное неравенство примет вид
. Исходное неравенство примет вид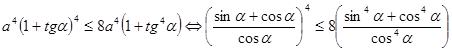 .
.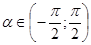 , то
, то 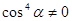 . Умножим обе части неравенства на
. Умножим обе части неравенства на 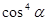 , получим
, получим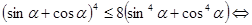
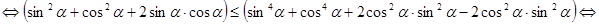
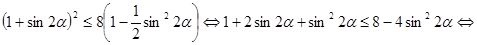
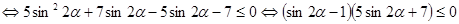 .
.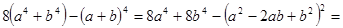
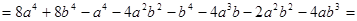
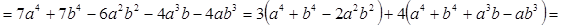
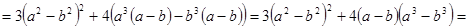
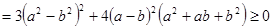 .
.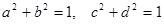 . Доказать, что
. Доказать, что 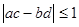 [9].
[9].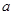 и
и 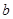 равна единице, то каждое из чисел
равна единице, то каждое из чисел 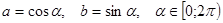 .
.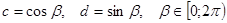 . Доказываемое неравенство запишется в виде
. Доказываемое неравенство запишется в виде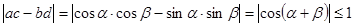 .
.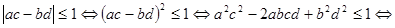
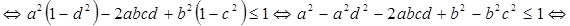
 .
.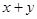 в области
в области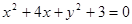 [25].
[25].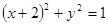 . Следовательно, каждое из выражений
. Следовательно, каждое из выражений 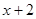 и
и 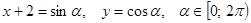 . Выразим
. Выразим 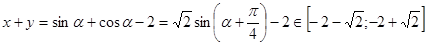 .
.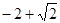 , наименьшее значение равно
, наименьшее значение равно 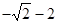 .
.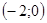 и радиусом
и радиусом 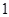 . Пусть в точке с координатами
. Пусть в точке с координатами 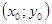 выражение
выражение 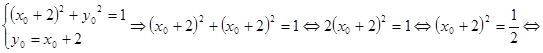
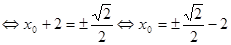 .
.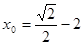 .
.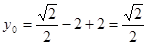 .
.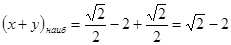 .
.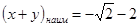 .
.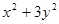 , если
, если 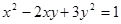 [24].
[24].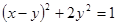 .
.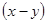 и
и 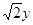 равна единице, поэтому каждое из этих выражений по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Вот почему можно положить
равна единице, поэтому каждое из этих выражений по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Вот почему можно положить 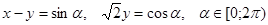 . Выразим сумму квадратов
. Выразим сумму квадратов 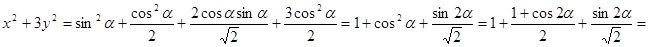
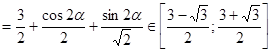 .
.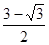 , наибольшее значение
, наибольшее значение 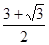 .
. , ответ можно получить, если найти множество всех ее значений. Хотя это и более общая задача, но ее решение оказывается более простым. Причем число
, ответ можно получить, если найти множество всех ее значений. Хотя это и более общая задача, но ее решение оказывается более простым. Причем число 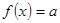 имеет хотя бы один корень. Поэтому требуется найти все такие значения параметра
имеет хотя бы один корень. Поэтому требуется найти все такие значения параметра 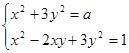 ,
,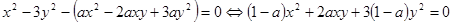 .
.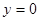 система решений не имеет, поэтому уравнение можно разделить на
система решений не имеет, поэтому уравнение можно разделить на 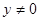
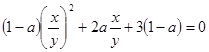 .
.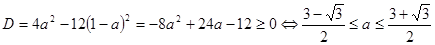 .
.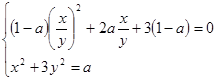 .
.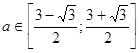 система имеет решения. Пусть
система имеет решения. Пусть 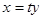 подставим во второе уравнение
подставим во второе уравнение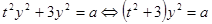 .
.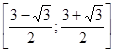 только положительные числа, значит, полученное уравнение имеет решения. Соответственно, имеет решение и вся система. Промежуток
только положительные числа, значит, полученное уравнение имеет решения. Соответственно, имеет решение и вся система. Промежуток 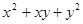 , если
, если 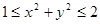 [16].
[16].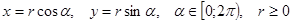 . Геометрический смысл такой замены: для каждой точки
. Геометрический смысл такой замены: для каждой точки 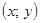 кольца
кольца 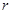 до начала координат и угол
до начала координат и угол 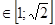 . Произведем замену в данном выражении
. Произведем замену в данном выражении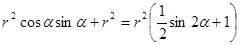 .
.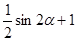 – это отрезок
– это отрезок 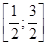 , то множество значений выражения
, то множество значений выражения 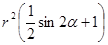 – отрезок
– отрезок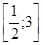 .
.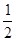 , наибольшее значение 3.
, наибольшее значение 3.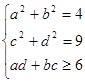 [42].
[42].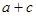 принимает наибольшее значение.
принимает наибольшее значение.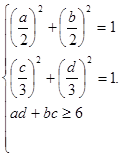
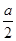 и
и 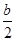 рана единице, то каждое из них по абсолютной величине не превосходит единицы, поэтому их можно рассматривать как синус и косинус некоторого аргумента. Вот почему будет законна подстановка
рана единице, то каждое из них по абсолютной величине не превосходит единицы, поэтому их можно рассматривать как синус и косинус некоторого аргумента. Вот почему будет законна подстановка 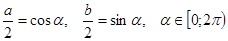 . Аналогично обосновывается введение замены
. Аналогично обосновывается введение замены 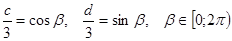 . Тогда неравенство системы перепишется в виде
. Тогда неравенство системы перепишется в виде
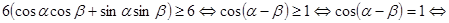
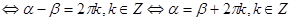 .
.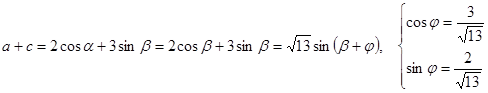 .
.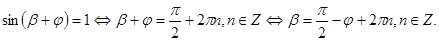
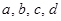
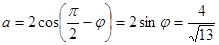 .
.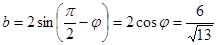 .
.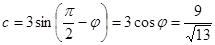 .
.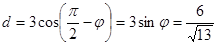 .
.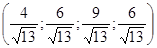 .
.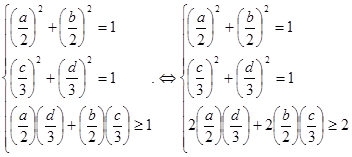 .
.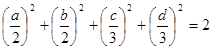 .
.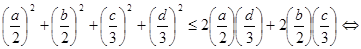
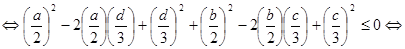
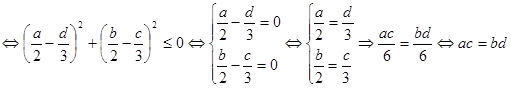 .
.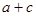
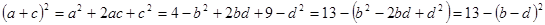 .
.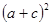 , а значит, наибольшее значение выражения
, а значит, наибольшее значение выражения 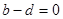 , то есть
, то есть 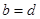 . Можно записать
. Можно записать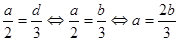 .
.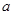 в первое уравнение исходной системы и найдем
в первое уравнение исходной системы и найдем 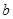
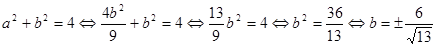 .
.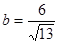 .
.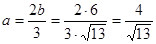 .
.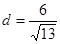 .
.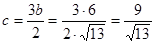 .
.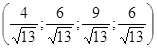 .
.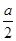 и
и 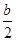 по модулю не превосходят единицы, можно проиллюстрировать графически. Уравнение
по модулю не превосходят единицы, можно проиллюстрировать графически. Уравнение 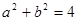 задает окружность с центром в начале координат и радиуса 2 .
задает окружность с центром в начале координат и радиуса 2 .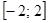 , тогда
, тогда 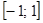 .
.
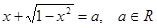 [45].
[45].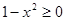 , то
, то 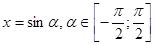 . Уравнение примет вид
. Уравнение примет вид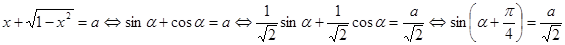 .
. , то данное уравнение корней не имеет.
, то данное уравнение корней не имеет.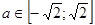 . Так как
. Так как 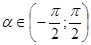 , то
, то 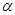 имеем
имеем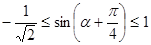 .
.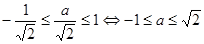 .
.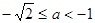 , то данное уравнение корней не имеет.
, то данное уравнение корней не имеет.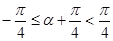 , то есть
, то есть 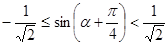 . Отсюда
. Отсюда 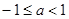 . Тогда данное уравнение имеет один корень
. Тогда данное уравнение имеет один корень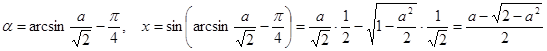 .
.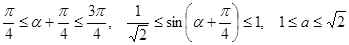 , то исходное уравнение имеет два корня
, то исходное уравнение имеет два корня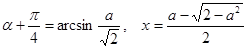 .
.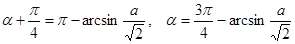 ,
,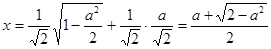 .
.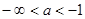 или
или 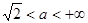 , то данное уравнение корней не имеет.
, то данное уравнение корней не имеет.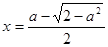 .
.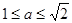 , то уравнение имеет два корня
, то уравнение имеет два корня 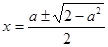 .
.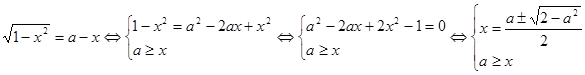 .
.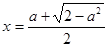 . Выясним, при каких значениях
. Выясним, при каких значениях 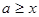 , то есть решим неравенство
, то есть решим неравенство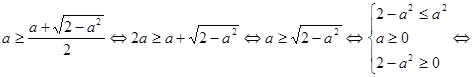
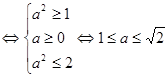 .
.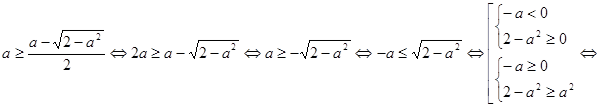
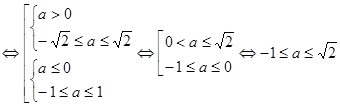 .
.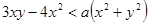
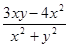 .
.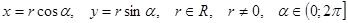 , тогда
, тогда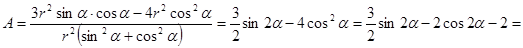
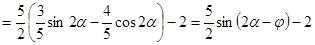 , где
, где 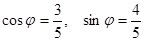 .
.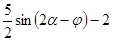
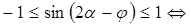
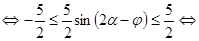
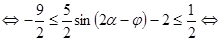
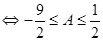 .
.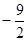 . Значит, при
. Значит, при 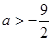 неравенство имеет решение.
неравенство имеет решение.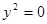 , то неравенство примет вид
, то неравенство примет вид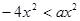 .
.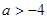 неравенство имеет решение.
неравенство имеет решение.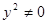 , получим
, получим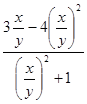 .
.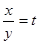 , тогда
, тогда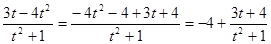 .
.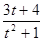 .
.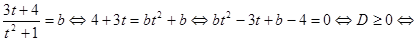
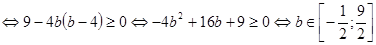 .
.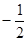 . Тогда наименьшее значение выражения
. Тогда наименьшее значение выражения 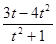 , а значит наименьшее значение выражения
, а значит наименьшее значение выражения 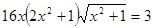 .
.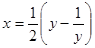 и возведением в квадрат. Решение задачи завершается тем, что заслушивается решение каждым способом, после чего происходит обсуждение сильных и слабых сторон каждого метода решения.
и возведением в квадрат. Решение задачи завершается тем, что заслушивается решение каждым способом, после чего происходит обсуждение сильных и слабых сторон каждого метода решения.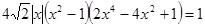 .
.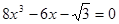 .
.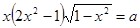 .
.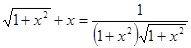 .
.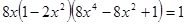 .
.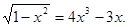
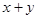 в области
в области 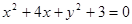 .
.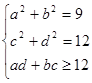 .
.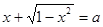 .
.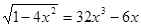 .
.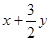 в области
в области 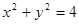 .
.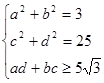 .
.