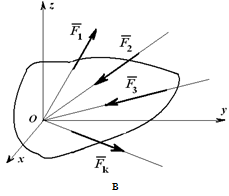
Три вида уравнений равновесия плоской системы (7 видео)

Содержание

Уравнение равновесия плоской системы сил
iSopromat.ru
Формы условий равновесия
Первая форма
Вторая форма
Третья форма
Другие условия равновесия
Три формы равновесия произвольной плоской системы сил.
🎬 Видео

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Уравнение равновесия плоской системы сил

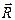
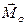
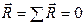
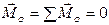
Условия равновесия плоской системы сил. Для равновесия плоской системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно любого произвольно выбранного центра О равнялись нулю, т. е.

, (7.8)

. (7.9)

В векторной форме условие (7.8) применять для решения задач неудобно. Спроектировав уравнение (7.8) на оси координат, получим вместе с (7.9) три следующих скалярных равенства:

; ; . (7.10)

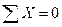
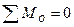
Систему (7.10) называют первой формой уравнений равновесия произвольной плоской системы сил, которая формулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую координатную ось (х, у) и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, равнялись нулю.

Вторая форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В и алгебраическая сумма проекций всех сил на какую-либо ось х или у, не перпендикулярную прямой АВ, равнялись нулю, т. е.

; ; (7.11)

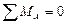
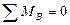
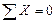
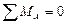
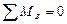
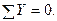
или ; ; (7.12)

Условие неперпендикулярности сил и прямой АВ также обязательно. В противном случае, одно из уравнений системы (7.11) или (7.12) не является независимым.

Третья форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно трех произвольных точек А, В и С, не лежащих на одной прямой, равнялись нулю, т. е.

; ; . (7.13)

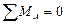
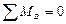
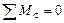
Если бы точки А, В и С лежали на одной прямой, то одно из уравнений не являлось бы независимым (его можно было получить из двух других путем тождественных преобразований). Решение задачи было бы равносильно решению системы двух уравнений с тремя неизвестными, что невыполнимо.

Все три формы уравнений равновесия совершенно равноправны. Отметим, что независимо от вида уравнений равновесия для плоской системы произвольно расположенных сил статика позволяет составить только три уравнения.

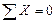
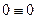
Условия равновесия плоской системы параллельных сил.Если силы перпендикулярны какой-либо оси х, то уравнение превращается в тождество . Для определения неизвестных сил остается два уравнения равновесия, которые можно представить в двух формах.

Первая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил и алгебраическая сумма моментов всех сил относительно произвольной точки О равнялись нулю, т. е.

; . (7.14)

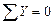
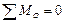
Вторая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В равнялись нулю, т.е.

; . (7.15)

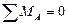
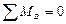
Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

iSopromat.ru

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Видео:§ 5.3. Уравнения равновесия плоской системы силСкачать

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Видео:§5 3 Уравнения равновесия плоской системы силСкачать

Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

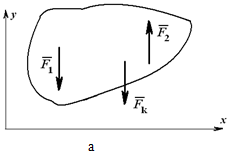
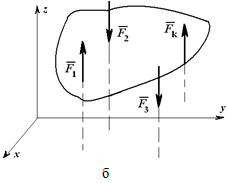
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Термех. Статика. Равновесие плоской произвольной системы силСкачать

Три формы равновесия произвольной плоской системы сил.

1. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси х и у равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки.

2.Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на одну из осей х или у равна нулю, а также, если равны нулю алгебраические суммы моментов всех сил относительно любых двух точек.

3.Произвольная плоская система сил находится в равновесии, если алгебраические суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой.

Пространственная система сил.

Пространственная система сил – это система сил, как угодно расположенных в пространстве.

Суммой трех сил, сходящихся в одной точке является сила по величине и направлению, совпадающая с диагональю параллелепипеда, построенного на заданных силах.

Момент силы относительно оси равен произведению модуля силы на кратчайшее расстояние от выбранной оси до линии действия силы.

Момент может равняться нулю, если:

1. Сила лежит на выбранной оси.

2.Сила пересекает выбранную ось.

3.Сила параллельна оси.

При приведении пространственной системы сил к точке, её можно заменять на эквивалентную систему с главным вектором и главным моментом.

Главный вектор – это геометрическая сумма всех сил системы.

Главный момент – это сумма моментов, компенсирующих пар.

Пространственная система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси x, y, z равны нулю, а также равны нулю моменты всех сил относительно этих же осей.

Кинематика.

Кинематика изучает виды движения.

Плоско – параллельное движение.

Плоско – параллельное движение – это такое движение, при котором фигура полученная пересечением данного тела с выбранной плоскостью остается параллельной самой себе за все время движения.

При плоско – параллельном движении всегда существует точка, абсолютная скорость которой в данный момент времени равна нулю. Каждый последующий момент – это будет другая точка.

ДИНАМИКА.

Динамика изучает виды движения тела в зависимости от приложенных сил.

1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.

2. Ускорение тела прямопропорциональных действующей на тело силе.

3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.

4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.

Центр тяжести – это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения.

Сила инерции.

Сила инерции – всегда направлена в противоположную сторону ускорению и приложена к связи.

При равномерном движении, т.е. когда а=0 сила инерции равна нулю.

При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.

Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил. F+R+Pu=0

Сила трения.

Трение делится на два вида: трение скольжения и трение качения.

Законы трения скольжения:

1. Сила трения прямопропорциональной нормальной реакции опоры и направлена вдоль соприкасающихся поверхностей в противоположную сторону движению.

2.Коэффициент трения покоя всегда больше коэффициента трения движения.

3. Коэффициент трения скольжения зависит от материала и физически – механических свойств трущихся поверхностей.

Условие самоторможения.

Трение приводит к снижению срока службы деталей к их износу и нагреву. Для того, чтобы этого избежать необходимо вести смазку. Повысить качество обработки поверхности деталей. В трущихся местах применять другие материалы.

4. По возможности заменить трение скольжения трением качения.

Основные понятия сопротивления материалов.

Сопротивление материалов – это наука, изучающая методы расчета конструкций на прочность, жесткость и устойчивость.

Прочность – это способность конструкции выдерживать заданную нагрузку в течение срока службы без разрушения и появления остаточных деформаций.

Жесткость – это способность конструкции сохранять первоначальную форму упругого равновесия.

Устойчивость – это способность конструкции сохранять первоначальную форму упругого равновесия.

Все тела разделены на 3 группы:

1.Брус – это тело, один из размеров которого (длина) во много раз больше двух других.

2. Оболочка – это тело, один из размеров которого (толщина) во много раз больше двух других.

3. Массив – это тела, все размеры которого равны.

Классификация нагрузок:

1.По характеру действия:

2. По способу приложения:

Метод сечения.

Мысленно разрезаем нагруженный силами груз, для того, чтобы определить внутренние силовые факторы, для этого отбрасываем одну часть груза. Заменяем межмолекулярную систему сил эквивалентной системой с главным вектором и главным моментом. При разложении главного вектора и главного момента по осям x, y, z. устанавливаем вид деформации.

Внутри сечения бруса может возникать внутри силовых факторов, если возникает сила N (продольная сила), то брус растянут или сжат.

Если возникает Мк (крутящий момент) то деформация кручения, сила Q (поперечная сила) то деформация сдвига среза или изгиба. Если возникает Мих и Миz (изгибающий момент) то деформация изгиба.

Метод сечения позволяет определить напряжение в сечении груза.

Напряжение – это величина, показывающая, сколько нагрузки приходится на единицу площади сечения.

Эпюра – это график изменения продольных сил , напряжений, удлинений, крутящих моментов и т. д.

Растяжение (сжатие) – это такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила.

Правила знаков для нагрузки.

Если нагрузка направлена от сечения бруса, то продольная сила будет равна ей со знаком «плюс», если нагрузка направлена к сечению, то продольная сила будет со знаком «минус».

В пределах упругих деформаций нормальное напряжение прямо – пропорционально продольным деформациям.

Е – модуль Юнка, коэффициент, который характеризует жесткость материала при напряжениях, зависит от материала, образца из справочных таблиц.

Нормальное напряжение измеряется в Паскалях.

Расчет на прочность. Np≥[N] -Условие прочности при растяжении – сжатии.

Np – расчетный коэффициент запаса прочности.

[n] – допустимый коэффициент запаса прочности.

бmax – расчет максимального напряжения.

Кручение.

Кручение – такой вид деформации, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор – крутящий момент. Кручению повергаются валы, оси. И пружины. При решении задач строятся эпюры крутящих моментов.

Правило знаков для крутящих моментов: Если вращающий момент поворачивает вал со стороны сечения по ходу часовой стрелки, то крутящий будет ему равен со знаком +, против – со знаком -.