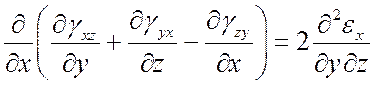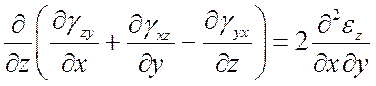Три группы уравнений теории упругости

Страницы работы

Содержание работы

Государственное образовательное учреждение
высшего профессионального образования

«ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
МИНИСТЕРСТВА ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ»
______________________________________________________________

А. В. Бенин Н. И. Невзоров И. И. Рыбина

ОБРАТНАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ

Бенин А.В., Невзоров Н.И., Рыбина И.И.

Представлены основные уравнения теории упругости, основные граничные задачи и способы их решения; варианты задания на выполнение расчетно-графической работы и примеры выполнения.

Для студентов строительных специальностей всех и форм обучения в ПГУПС.

Обратная задача теории упругости.

1. Теоретические положения.

Основные уравнения теории упругости образуют три группы соотношений, отражающих статическую, геометрическую и физическую сторону задачи.

1.1. Статические уравнения.

К этой группе относятся дифференциальные уравнения равновесия (уравнения Навье)

(1)

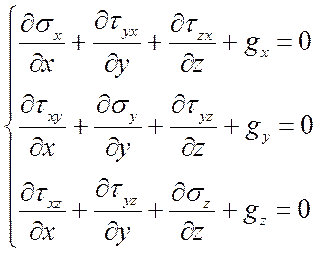
и соотношения, выражающие свойство парности касательных напряжений

(2)

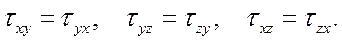
В эту же группу входят уравнения равновесия элементарного тетраэдра (формулы Коши):

(3)

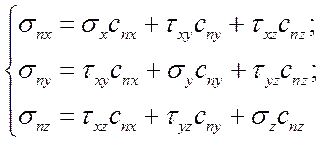
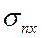
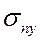
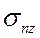
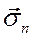
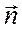
при помощи которых можно определить проекции , , полного напряжения , действующего по наклонной площадке с нормалью , на оси декартовой системы координат. Если рассматриваемая площадка тетраэдра примыкает к поверхности тела, то в левой части (3) появляются проекции поверхностных сил, действующих на тело:

(3 * )

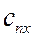
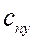
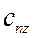
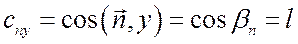
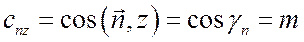
В (3) и (3 * ) через , и обозначены направляющие косинусы нормали к площадке. В технической литературе для обозначения направляющих косинусов часто используют и другие обозначения:

;

;

.

Уравнения (3 * ) используют для записи в напряжениях граничных условий (условий на поверхности тела), связывающих поверхностную нагрузку с напряжениями.

Важную роль (при постановке граничных условий, в технических дисциплинах, таких как сопротивление материалов) играют условия статической эквивалентности – интегральные зависимости между внутренними усилиями, действующими в поперечном сечении стержня, и напряжениями (рис. 1):

, ,

, , (4)

, .

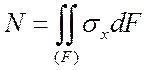
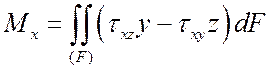
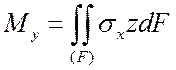
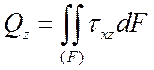
В этом примере ось x системы координат совпадает с осью стержня. Для того, чтобы записать условия статической эквивалентности в другой системе координат, достаточно произвести циклическую перестановку индексов в (4): .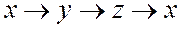

В полную систему уравнений для решения задач теории упругости из статических соотношений входят три дифференциальных уравнения равновесия (1), содержащие шесть (с учетом свойства парности касательных напряжений) неизвестных.

1.2. Геометрические соотношения.

В этой группе в первую очередь следует выделить уравнения Коши, связывающие между собой упругие перемещения и относительные деформации:

(5)

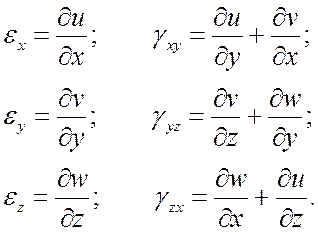
При известных перемещениях u, v, w относительные деформации непосредственно определяются согласно (4). Задача нахождения перемещений по известным относительным деформациям существенно сложнее, поскольку для определения трех неизвестных функций имеется шесть уравнений (система переопределена). Необходимы дополнительные условия, обеспечивающие интегрируемость системы (4). Такими условиями являются уравнения Сен-Венана:

,

, (6)

,

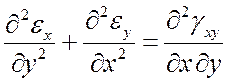
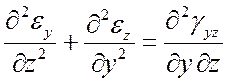
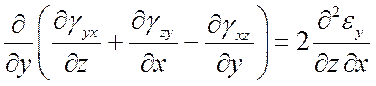
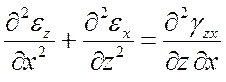
Физический смысл уравнений Сен-Венана – условие сплошности деформируемого тела; математический – условие интегрируемости уравнений Коши.

В полную систему уравнений теории упругости входят шесть уравнений Коши, содержащие шесть неизвестных.

1.3. Физические уравнения.

В линейной теории упругости, когда напряжения не превосходят предела пропорциональности, напряжения и деформации связывают между собой при помощи обобщенного закона Гука.

Прямая форма записи:

(7)

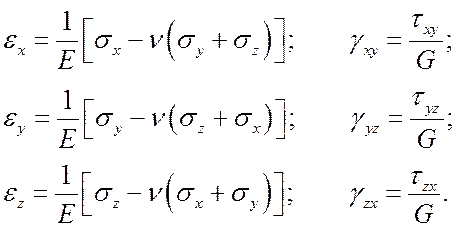
— E – модуль Юнга (модуль нормальной упругости, модуль упругости первого рода);

— n — коэффициент Пуассона;

— G – модуль упругости при сдвиге (модуль упругости второго рода).

Для однородного изотропного материала существует связь между этими упругими постоянными:

.

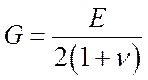
Закон Гука в обратной форме:

(8)

— — коэффициент Ламе;

— — относительное изменение объема (объемная деформация).

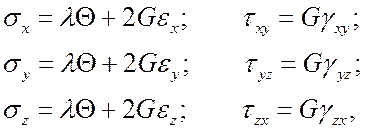
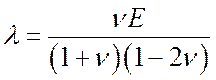
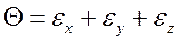
1.4. Общая система уравнений теории упругости.
Прямая и обратная задачи.

Разрешающую систему уравнений теории упругости образуют:

— дифференциальные уравнения равновесия (три уравнения, шесть неизвестных напряжений);

— уравнения Коши (шесть уравнений, шесть неизвестных относительных деформаций и три неизвестных перемещения);

— уравнения закона Гука (шесть уравнений).

Таким образом, для определения пятнадцати неизвестных имеется пятнадцать уравнений. Если одновременно используются все пятнадцать уравнений, не нужны уравнения совместности Сен-Венана, поскольку они непосредственно следуют из уравнений Коши. Найденные в результате интегрирования функции должны удовлетворять граничным условиям (3 * ).

Принято различать два основных типа задач теории упругости.

1. Прямая задача. Заданы объемные и поверхностные силы. Требуется определить все упругие перемещение, напряжения и относительные деформации во всех точках рассматриваемого тела, включая его границу (поверхность).

Прямая задача теории упругости представляет наибольший практический интерес, однако ее решение чрезвычайно трудное из-за необходимости интегрировать сложную систему уравнений в частных производных и, главное, удовлетворять разнообразным граничным условиям.

В зависимости от вида граничных условий прямые задачи теории упругости подразделяют на следующие:

1) первая основная задача – на границе тела заданы поверхностные силы;

2) вторая основная задача – заданы перемещения точек поверхности тела;

3) смешанная задача – на одной части поверхности заданы поверхностные силы, на остальной части – перемещения.

Обычно при решении прямой задачи полную систему уравнений теории упругости используют не непосредственно, а в преобразованном виде.

Наибольшее теоретическое и практическое развитие получили следующие два способа преобразования исходной системы уравнений.

1) За основные неизвестные принимают упругие перемещения u, v, w. Относительные деформации записывают через перемещения по уравнениям Коши, результат подставляют в закон Гука, выражая тем самым напряжения через перемещения; в свою очередь полученные соотношения подставляют в уравнения Навье. Таким образом, решение задачи сводится к трем дифференциальным уравнениям, записанным относительно трех неизвестных перемещений. Такой метод называется решением в перемещениях.

2) За основные неизвестные принимают шесть составляющих напряжений. Деформации выражают через напряжения при помощи закона Гука, результат подставляют в уравнения совместности Сен-Венана. Полученная система уравнений совместно с уравнениями Навье позволяет определить напряжения. Такой подход называется решением в напряжениях.

2. Обратная задача. Заданы функции, описывающие или упругие перемещения, или относительные деформации, или напряжения во всех точках рассматриваемого тела. Необходимо найти остальные неизвестные компоненты, в том числе объемные силы и условия на поверхности.

Решение обратной задачи всегда может быть получено, поскольку нет необходимости интегрировать сложную систему дифференциальных уравнений в частных производных, все сводится к простейшим математическим операциям.

Видео:Лекция №1 Постановка задачи теории упругости. Условия совместности деформаций Сен-Венана.Скачать

Лекция 1. Основы теории упругости

1.1 Основные положения, допущения и обозначения

Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть проверены решения, полученные с использованием допущений сопротивления ма­териалов, и установлены границы применимости этих решений. Иногда разделы теории упругости, в которых, как и в сопротив­лении материалов, рассматривается вопрос о пригодности де­тали, но с использованием достаточно сложного математического аппарата (расчет пластин, оболочек, массивов), относят к при­кладной теории упругости.

В настоящей главе изложены основные понятия математиче­ской линейной теории упругости. Применение математики к опи­санию физических явлений требует их схематизации. В математической теории упругости задачи решаются с возможно меньшим числом допущений, что усложняет мате­матические приемы, применяемые для решения. В линейной тео­рии упругости предполагается существование линейной зави­симости между составляющими напряжениями и деформациями. Для ряда материалов (резина, некоторые сорта чугуна) такая зависимость даже при малых деформациях не может быть принята: диаграмма s — e в пределах упругости имеет одинако­вые очертания как при нагружении , так и при разгрузке, но в обоих случаях криволинейна. При исследовании таких материалов необходимо пользоваться зависимостями нелинейной теории упру­гости.

В математической линейной теории упругости исходят из следующих допущений:

1. О непрерывности ( сплошности ) среды. При этом атомистическая структура вещества или наличие каких-либо пустот не учитывается.

2. О естественном состоянии, на основании которого началь­ное напряженное (деформированное) состояние тела, возникшее до приложения силовых воздействий, не учитывается, т. е. предполагается, что в момент нагружения тела деформации и напряжения в любой его точке равны нулю. При наличии на­чальных напряжений это допущение будет справедливым, если только к результирующим напряжениям (сумме начальных и возникших от них из воздействий) могут быть применены зависимости линейной теории упругости.

3. Об однородности, на основании которого предполагается, что состав тела одинаков во всех точках. Если применительно к металлам это допущение не дает больших погрешностей, то в от­ношении бетона при рассмотрении малых объемов оно может при­вести к значительным погрешностям.

4. О шаровой изотропности , на основании которого считается, что механические свойства материала одинаковы по всем направ­лениям. Кристаллы металла не обладают таким свойством, но для металла в целом, состоящего из большого числа мелких кри­сталлов, можно считать, что эта гипотеза справедлива. Для ма­териалов, обладающих различными механическими свойствами в разных направлениях, как, например, для слои­стых пластиков, разработана теория упругости ортотропных и анизотропных материалов.

5. Об идеальной упругости, на основании которого предпола­гается полное исчезновение деформации после снятия нагрузки. Как известно, в реальных телах при любом нагружении возникает остаточная деформация. Поэтому допущение следует считать при­менимым, если остаточная деформация не превышает условно заданной нормы.

6. О линейной зависимости между составляющими деформа­циями и напряжениями.

7. О малости деформаций, на основании которого предпола­гается, что относительные линейные и угловые деформации малы по сравнению с единицей. Для таких материалов, как резина, или таких элементов, как спиральные пружины, создана теория больших упругих деформаций.

При решении задач теории упругости пользуются теоремой о единственности решения: если заданные внешние поверхностные и объемные силы находятся в равновесии, им соответствует одна единственная система на­пряжений и перемещений. Положен ие о е динственности решения справедливо, если только справедливы допущение о естественном состоянии тела (иначе возможно бесчисленное количество решений) и допущение о линейной зависимости между деформациями и внешними силами.

При решении задач теории упругости часто пользуются принци­пом Сен-Венана: если внешние силы, приложенные на небольшом участке упругого тела, заменить действующей на том же участке статически эквивалентной си­стемой сил (имеющей тот же главный вектор и тот же главный момент), то эта замена вызовет лишь изменение местных де­формаций.

В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения мало зависят от способа их приложения. Нагрузка, которая в курсе сопротивления мате­риалов схематически выражалась на основании принципа Сен-Венана в виде силы или сосредоточенного момента, на самом деле представляет собой нормальные и касательные напряжения, распределенные тем или иным способом на определенном участке поверхности тела. При этом одной и той же силе или паре сил может соответствовать различное распределение напряже­ний. На основании принципа Сен-Венана можно считать, что из­менение усилий на участке поверхности тела почти не отражается на напряжениях в точках, удаленных на достаточно большое расстояние от места приложения этих усилий (по сравнению с линейными размерами нагруженного участка).

Положение исследуемой площадки, выделенной в теле (рис. 1), определяется направляющими косинусами нормали N к пло­щадке в выбранной системе прямоугольных осей координат х , у и z .

Если Р — равнодействующая внутренних сил, действующих по элементарной площадке , выделенной у точки А , то полное напряжение р _N в этой точке по площадке с нормалью N опре­деляется как предел отношения в следующей форме:

.

Вектор р _N можно разложить в пространстве на три взаимно перпендикулярные составляющие.

1. На составляющие р _Nx , р _Ny и р _Nz по направлениям трех осей (рис. 1, а). Эти состав­ляющие положительны, если совпадают по направлению с поло­жительными направлениями соответствующих осей. Согласно рис. 1, а

. (1.1,а)

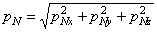
2. На составляющие , и по направлениям нормали к площадке (нормальное напряжение) и двух взаимно перпенди­кулярных осей s и t (рис. 1,б), лежащих в плоскости площадки (касательные напряжения). Согласно рис.1, б

. (1.1,б)

Если сечение тела или площадка параллельны одной из плоскостей координат, например у0 z (рис. 2), то нормалью к этой площадке будет третья ось координат х и составляющие напря­жения будут иметь обозначения , и .

Нормальное напряжение положительно, если оно растяги­вающее, и отрицательно, если оно сжимающее. Знак касатель­ного напряжения определяется с помощью следующего правила: если положительное (растягивающее) нормальное напряжение по площадке дает положительную проекцию, то касательное на­пряжение по той же площадке считается положительным при условии, что оно тоже дает положительную проекцию на соот­ветствующую ось; если же растягивающее нормальное напря­жение дает отрицательную проекцию, то положительное касательное напряжение тоже должно давать отрицательную про­екцию на соответствующую ось.

На рис. 3, например, все составляющие напряжения, дейст­вующие по граням элементарного параллелепипеда, совпадаю­щим с плоскостями координат, положительны.

Чтобы определить напряженное состояние в точке упругого тела, необходимо знать полные напряжения р _N по трем взаимно перпендикулярным площадкам, проходящим через эту точку. Так как каждое полное напряжение можно разложить на три составляющие, напряженное состояние будет определено, если будут известны девять составляющих напряжений. Эти составляю­щие можно записать в виде матрицы

,

называемой матрицей компонентов тензора напряжений в точке.

В каждой горизонтальной строчке матрицы записаны три со­ставляющих напряжения, действующих по одной площадке, так как первые значки (название нормали) у них одинаковые. В каждом вертикальном столбце тензора записаны три напря­жения, параллельных одной и той же оси, так как вторые значки (название оси, параллельно которой действует напряжение) у них одинаковые.

1.2 Уравнения равновесия элементарного параллелепипеда и элементарного тетраэдра

Выделим у исследуемой точки А (с координатами х , у и z ) напря­женного упругого тела тремя взаимно перпендикулярными па­рами плоскостей элементарный параллелепипед с размерами ребер dx , dy и dz (рис. 2). По каждой из трех взаимно перпен­дикулярных граней, примыкающих к точке А (ближайших к пло­скостям координат), будут действовать три составляющих напря­жения — нормальное и два касательных. Считаем, что по граням, примыкающим к точке А , они положительны.

При переходе от грани, проходящей через точку А , к парал­лельной грани напряжения меняются и получают приращения. Например, если по грани CAD , проходящей через точку А , дей­ствуют составляющие напряжения = f ₁ ( x , y , z ), = f ₂ ( x , y , z ,), = f ₃ ( x , y , z ,), то по параллельной грани, вслед­ствие приращения только одной координаты х при переходе от одной грани к другой, будут действовать составляющие напря­жения Можно определить напряжения на всех гранях элементарного паралле­лепипеда, как показано на рис. 3.

Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, У и Z. Если приравнять нулю сумму проекций на ось х всех нормальных, касательных и объемной сил, дейст­вующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение

.

Составив аналогичные уравнения проекций сил на оси у и z , напишем три дифференциальных уравнения равновесия элементар­ного параллелепипеда, полученных Коши,

. (1.2)

При уменьшении размеров параллелепипеда до нуля он прев­ращается в точку, а и представляют собой составляющие напряжения по трем взаимно перпендикулярным площадкам, проходящим через точку А.

Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси x _c , парал­лельной оси х и проходящей через его центр тяжести, получим уравнение

или, с учетом того, что второй и четвертый члены уравнения выс­шего порядка малости по сравнению с остальными, после сокра­щения на dxdydz

или .

Составив аналогичные уравнения моментов относительно цен­тральных осей у _c и z_c , получим три уравнения закона парности касательных напряжений

, , . (1.3)

Этот закон формулируется так: касательные напряжения, действующие по взаимно перпендикулярным площадкам и направ­ленные перпендикулярно к линии пересечения площадок, равны по величине и одинаковы по знаку.

Таким образом, из девяти составляющих напряжений матрицы тензора шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следую­щие шесть составляющих напряжений:

.

Но составленные условия равновесия дали нам всего лишь три уравнения (1.2), из которых шесть неизвестных найдены быть не могут. Таким образом, прямая задача определения напряжен­ного состояния в точке в общем случае статически неопределима. Для раскрытия этой статической неопределимости необходимы дополнительные геометрические и физические зависимости.

Рассечем элементарный параллелепипед у точки А плоскостью, наклоненной к его граням; пусть нормаль N к этой плоскости имеет направляющие косинусы l , т и п. Полу­чившаяся геометрическая фигура (рис. 4) представляет собой пирамиду с треугольным основанием — элементарный тетраэдр. Будем считать, что точка А совпадает с началом координат, а три взаимно перпендикулярные грани тетраэдра — с плоскостями координат.

Составляющие напряжения, действующие по этим граням тетраэдра, будем считать положительными. Они показаны на рис. 4. Обозначим через и проекции полного напря­жения p_N , действующего по наклонной грани BCD тетраэдра, на оси х , у и z . Площадь наклонной гра­ни BCD обозначим dF . Тогда площадь грани АВС будет dF , грани ACD — dF и грани А D В — dF .

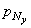
Составим уравнение равновесия тетраэдра, спроектировав все силы, действующие по его гра­ням, на ось х ; проекция объемной силы в уравне­ние проекций не входит, так как представляет собой величину высшего порядка малости по сравнению с проекциями поверхностных сил:

,

.

Составив уравнения проекции сил, действующих на тетраэдр, на оси у и z , получим еще два аналогичных уравнения. В результате будем иметь три уравнения равновесия элементар­ного тетраэдра

. (1.4)

По известным трем проекциям найдем полное напряжение

. (1.5)

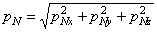
Разделим пространственное тело произвольной формы систе­мой взаимно перпендикулярных плоскостей хОу , y О z и хО z (рис. 5) на ряд элементарных параллелепипедов. У поверхности тела при этом образуются элементарные тетраэдры, (криволинейные участки по­верхности ввиду их малости можно заменить плоскостями). В та­ком случае р _N будет представлять нагрузку на поверхности, а уравнения (1.4) будут связывать эту нагрузку с напряжениями и в теле, т. е. будут представлять граничные условия задачи теории упругости. Условия, определяемые этими уравнениями, называют условиями на поверхности.

Следует отметить, что в теории упругости внешние нагрузки представляются нормальными и касательными напряжениями, приложенными по какому-либо закону к площадкам, совпадаю­щим с поверхностью тела.

1.3 Нормальные и касательные напряжения по наклонной площадке

Рассмотрим элементарный тетраэдр ABCD , три грани которого параллельны координатным плоскостям, а нормаль N к четвертой грани составляет с координатными осями углы, косинусы ко­торых равны l , т и п (рис. 6). Будем считать заданными составляющие нормальные и касательные напряжения, действующие по площадкам, лежащим в координатных плоскостях, и определим напряжения на площадке BCD . Выберем новую систему прямо­угольных осей координат х ₁ , y ₁ и z ₁, так чтобы ось х₁ совпадала с нормалью N , а оси у₁ и z ₁ лежали в плоскости площадки BCD . Каждая из этих осей будет иметь в системе осей x , y , z свои направляющие косинусы, указанные в табл. 1.

Видео:Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать

Три группы уравнений теории упругости

9.7. Постановка плоской задачи теории упругости методами МКЭ

9.7.1. Основные понятия

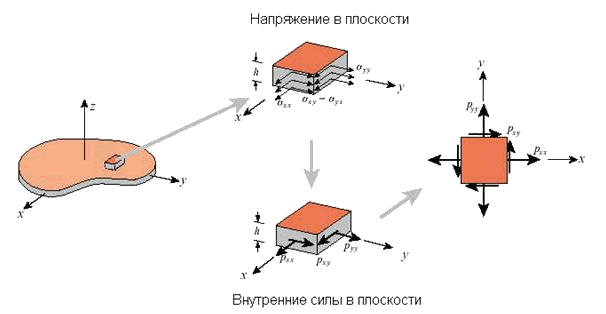
Плоская задача теории упругости является наиболее подходящим примером для демонстрации алгоритма МКЭ применительно к решению многомерных задач механики сплошных сред. Базовые соотношения и особенности алгоритма метода конечных элементов в данном случае существенно отличаются от расчета одномерных задач (растяжения, кручения и изгибы стержней).

В механике конструкций плоский тонкий лист материала называется пластиной. Расстояние между верхней и нижней поверхностью пластины называется толщиной и обозначается через h . Пластина имеет также срединную плоскость, лежащую между двух поверхностей. Направление перпендикулярное срединной плоскости называется трансверсальным . Как правило, глобальная ось z направлена перпендикулярно срединной плоскости, в то время как оси x и y лежат в срединной плоскости, образуя глобальную декартову систему координат (Рис. 9.49). Таким образом, уравнение срединной плоскости имеет вид: z=0.

Рис. 9.49. Двумерная конструкция в плоско-напряженном состоянии.

Для того чтобы пластина находилась в плоско-напряженном состоянии, необходимо чтобы выполнялись следующие условия:

Все внешние нагрузки: поверхностные, действующие на точки боковой поверхности пластины, и объемные, действующие на внутренние точки пластины, — перпендикулярны оси z , т.е. лежат в плоскости xy , и симметричны относительно срединной плоскости.

Все условия закрепления симметричны относительно срединной плоскости.

Внутренние перемещения, деформации и напряжения принимаются постоянными по толщине пластины.

Нормальные и сдвиговые компоненты тензора напряжений в направлении оси z равны нулю или пренебрежимо малы.

Пластина изготовлена из материала, не меняющего своих свойств по толщине. Такие пластины называются трансверсально-однородными.

Заметим, что 3 и 4 предположения не являются необходимым следствием первых двух. Чтобы они выполнялись толщина h должна быть достаточно малой, обычно не более 10% наименьшего характерного размера пластины в срединной плоскости. Кроме того, если толщина пластины изменяется, то это изменение должно быть достаточно плавным . И, наконец, геометрия пластины должна быть симметричной относительно срединной плоскости.

Последнее предположение очевидно исключает из рассмотрения плоские композиционные конструкции, типа ячеистых сотоподобных структур или сендвич-структур . Разработка моделей таких конструкций требует достаточно сложного интегрирования по толщине пластины, а также учета эффектов изгиба и растяжения, и в данном курсе рассматриваться не будет.

Замечание 1. Нагрузка перпендикулярная срединной плоскости приводит к напряженному состоянию, называемому изгибом пластины, описываемому дифференциальным уравнением IV-го порядка относительно прогиба пластины. Алгоритм МКЭ в этом случае имеет принципиально иной характер, поскольку данная задача относится к классу одномерных задач.

Замечание 2. Если принято, что напряжения вдоль оси z имеют место, то состояние пластины носит название обобщенного плоско-напряженного состояния.

Замечание 3. Кроме плоско-напряженного состояния в теории упругости широко применяется понятие плоско-деформированного состояния, согласно которому деформация вдоль оси z равна нулю. Физически это соответствует протяженным конструкциям, нагруженным силами перпендикулярно оси z . Например, плотина, дамба или лопатка ротора генератора при некоторых допущениях.

9.7.2. Математическая модель

Математическая модель пластины в плоско-напряженном состоянии есть двумерная краевая задача теории упругости, заданная в области с границей Г, как показано на рис. 9.50.

Все основные переменные, входящие в исходные уравнения, представляют собой функции двух переменных x и y и считаются осредненными по толщине пластины. Например, внешние силы, действующие в области и входящие в правую часть уравнения движения точек сплошной среды, есть не что иное, как интегралы по толщине пластины от заданных объемных сил.

Рис. 9.50. Математическая модель пластины в плоско-напряженном состоянии.

9.7.3. Исходные данные

Исходные данные включают в себя следующие объекты:

Геометрия области. Геометрия тела представляет собой область с границей Г, показанную на рис. 9.50.

Толщина пластины. Во многих случаях пластины, используемые как конструктивные элементы, имеют постоянную толщину. Если же толщина пластины изменяется, то толщина есть функция двух пространственных координат h=h ( x,y ), при этом для сохранения плоско-напряженного состояния изменение толщины должно быть достаточно медленным.

Материал пластины. Свойства материала задаются с помощью определяющих соотношений. В данной лекции мы рассмотрим случай линейно упругого, но не обязательно изотропного материала.

Силы, действующие в области . «Областные» силы действуют на внутренние точки области . В общем случае они могут быть двух типов. Во-первых, стандартные объемные силы, определенные как силы, действующие на единицу объема пластины, например, вес тела. Во-вторых, специфические областные силы, действующие по касательной к верхней и нижней поверхностям пластины, например, силы трения, которые могут возникать при относительном движении пластины по другому телу. Эти силы определенным образом должны быть приведены к срединной плоскости пластины.

Заданные поверхностные силы. Поверхностные силы – это известные силы, действующие на точки границы Г. Часто они называются поверхностными усилиями. При решении технических задач необходимо обращать внимание на размерность этих сил, т.к. они могут быть заданы как сила на единицу поверхности или как сила на единицу длины.

Кинематические граничные условия. Кинематические граничные условия задают способы закрепления пластины. Точки на границе области могут быть зафиксированы в одном или в двух направлениях. Дополнительно могут быть заданы условия симметрии или антисимметрии . Если кинематические граничные условия не заданы, то такие граничные условия называются свободными.

9.7.4. Искомые функции

В задачах механики основными неизвестными величинами являются поля перемещений, деформаций и напряжений. Согласно ранее сделанным предположениям, все основные искомые физические переменные не зависят от нормальной координаты z и являются функциями только координат x и y .

Перемещения. Вектор перемещений состоит из двух компонент:

. (9.14)

Нормальная компонента перемещений u _z ( x , y , z ) в общем случае отлична от нуля из-за эффекта коэффициента Пуассона и зависит от z . Однако это перемещение не входит в разрешающее уравнение задачи и может быть вычислено отдельно по найденным основным компонентам.

Деформации. Деформации, лежащие в плоскости, формируют тензор, определяемый тремя независимыми компонентами: , и . Для удобства формулировки конечно-элементных уравнений матричной формы компоненты тензора деформации представим в виде трехкомпонентного «вектора деформации»:

. (9.15)

Удвоенная компонента представляет собой деформацию сдвига и используется для сокращения записи выражения энергии деформации. Остальные сдвиговые компоненты и равны нулю согласно исходным предположениям. Нормальная компонента обычно не равна нулю из-за эффекта Пуассона. Однако также как перемещение нормальная компонента деформации не входит в разрешающее уравнение как неизвестная. В выражении энергии деформации произведение обращается в ноль, поскольку нормальное напряжение равно нулю по исходным предположениям.

Напряжения. Тензор напряжений также определяется тремя независимыми компонентами , и , лежащими в плоскости пластины. Как и в случае с деформациями для удобства представления конечно-элементных уравнений в матричном виде сформируем трехкомпонентный «вектор напряжений»:

. (9.16)

Оставшиеся три компонента тензора напряжений , и равны нулю согласно определению плосконапряженного состояния.

Объемные внутренние силы могут быть получены путем интегрирования напряжений по толщине пластины. В случае однородного распределения напряжений по координате z , данные силы, также образующие тензор, легко могут быть вычислены согласно следующей формуле:

, , . (9.17)

В литературе такие силы часто называются мембранными силами (рис. 9.51).

Рис. 9.51. Внутренние силы и напряжения, действующие на произвольный элемент мембраны.

9.7.5. Разрешающие уравнения

Система разрешающих уравнений классической линейной теории упругости схематично представлена на рис. 9.52 в виде так называемой диаграммы Тонти .

Рис. 9.52. Система разрешающих уравнений классической линейной теории упругости в виде диаграммы Тонти .

Система разрешающих уравнений теории упругости относительно трех неизвестных физических полей перемещений, деформации и напряжений состоит из трех групп уравнений: кинематических соотношений, определяющих уравнений и уравнений равновесия в области тела. При отсутствии начальных напряжений в теле эта система уравнений может быть записана в следующем символьно-матричном виде:

, (9.18а)

(9.18б)

(9.18в)

Кроме уже введенных матричных векторов перемещений, деформаций и напряжений, записанная система трех матричных уравнений содержит вектор объемных сил с компонентами b_x , b_y , входящий в уравнение равновесия, матрицу упругих модулей с компонентами E_ij , связывающую напряжения и деформации в точке тела, а также две символические матрицы, состоящие из частных производных по пространственным координатам. Заметим, что символические матрицы, входящие в кинематическое соотношение и в уравнение равновесия, совпадают с точностью до операции транспонирования.

В матричном виде система (4.5) может быть представлена в следующем виде:

(9.19)

где E – симметричная матрица упругих модулей, D – символическая матрица, состоящая из частных производных, b – матричный вектор объемных сил.

Заметим, что приведенная система уравнений (9.19) несколько отличается от координатной или тензорной форм записи полной системы уравнений теории упругости, часто используемым в литературе. Достоинство данной формулировки состоит в том, что все уравнения уже записаны в матричном виде, наиболее удобном для вывода соотношений метода конечных элементов.

Если материал пластины является изотропным, то как известно из теории упругости компоненты матрицы упругих модулей E могут быть выражены через технические константы материала: модуль упругости E, коэффициент Пуассона и модуль сдвига G:

,

,

,

.

При этом напомним, что только две из перечисленных технических констант являются независимыми. Формула, связывающая модуль упругости E, коэффициент Пуассона и модуль сдвига G, имеет следующий вид:

.

9.7.6. Граничные условия

В классической задаче теории упругости граничные условия, заданные на поверхности Г, могут быть двух типов: кинематические граничные условия и силовые граничные условия. Предполагается, что каждый тип граничных условий задан на своей части поверхности: Г _u и Г_t соответственно (Рис. 9.53).

Рис. 9.53. Кинематические и силовые граничные условия в плоской задаче теории упругости.

Кинематические граничные условия заданы на части поверхности Г _u и могут быть записаны в следующей формуле:

(9.20)

Правая часть соотношения (9.20) представляет собой заданные перемещения точек поверхности. Во многих случаях эти перемещения равны нулю. Например, в случае, если часть поверхности каким-либо образом закреплена, как показано на рис. 9.53.

Силовые граничные условия заданы на части поверхности Г _t и могут быть записаны в следующей форме:

(9.21)

В формуле (9.21) правая часть представляет собой заданные поверхностные силы или поверхностные усилия, а левая часть – вектор напряжений на площадке с нормалью n .

Альтернативная форма записи силовых граничных условий может быть записана в виде:

(9.22)

где и .

Вектор напряжений на площадке с нормалью n определяется согласно формуле Коши через компоненты внешней нормали к поверхности и компоненты тензора упругости в точке поверхности:

, (9.23)

где n_x и n_y обозначают декартовы координаты единичной нормали к поверхности n ( e ) (направляющие косинусы). Таким образом (9.21) может быть записано в виде двух скалярных соотношений и .

В некоторых случаях бывает удобно записать условие (9.21) в локальной системе координат, образованной нормалью n i >> и ортом касательной t :

, (9.24)

где соответствующие компоненты напряжений в локальной системе координат могут быть выражены следующим образом:

,

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

📽️ Видео

Теория упругости. Лекция №3 (1). Постановка задачи теории упругости в перемещениях и в напряжениях.Скачать

Закон Гука и сила упругостиСкачать

Лекция №13 "Элементы теории упругости"Скачать

Теория упругости №4 (завершение). Понятие о плоской задаче теории упругости.Скачать

Леонтьев Н.Е. - Основы механики сплошных сред. Семинары - 7. Модель линейно-упругого телаСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Теория упругостиСкачать

Напряжения. Свободная энергия. СЕ. МКЭ. Тензор напряжений. Вектор напряжений. Теория упругости.Скачать

Общая физика | Лекция 22: Элементы теории упругости. Коэффициент Пуассона. Модули деформацийСкачать

Лекция IV-3. Напряженное состояние под внешней нагрузкой. Часть 1Скачать

Теория групп 3 - Подгруппы. Абелевы и неабелевы группы. Спонтанное нарушение симметрии.Скачать

Основы теории упругости. Принцип Сен-ВенанаСкачать

Лекция VII-3. Механика скальных грунтовСкачать

Лекция II-3. Теория прочности и пластичностиСкачать

Лекция №14 "Теория упругости (продолжение). Волны" (Булыгин В.С.)Скачать