Третий элемент a33 третьей строки обратной матрицы а 1 системы уравнений

Метод обратной матрицы является эффективным и часто используемым методом решения СЛАУ при применении систем линейных уравнений для решения задач планирования различных процессов. Его задействуют в случаях, в которых соблюдается условие: количество неизвестных совпадает с числом линейных уравнений системы.

Важным условием является соблюдение требования в отношении определителя основной матрицы, он не должен быть равен 0. В этом случае матрице А соответствует обратная матрица А–1. В матричной форме СЛАУ записывается в виде матричного равенства: А×Х = В.

Следующим шагом, который выполняет скрипт онлайн калькулятора, является операция умножения как левой, так и правой части, данного уравнения на матрицу А–1 слева. В результате преобразований осуществляется выход на конечное расчетное уравнение вычисления столбца данных с неизвестными Х = А–1×В.

Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

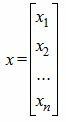(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда

Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:

или, учитывая, что Ex=x:

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Видео:Обратная матрицаСкачать

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

.

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

.

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

.

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

.

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

.

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

.

Пример 2. Решить следующую систему линейных уравнений матричным методом:

.

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

.

Вычислим все алгебраические дополнения матрицы A:

,

,

,

,

,

,

,

,

.

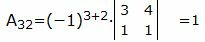Обратная матрица вычисляется из следующего выражения:

где A_ij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

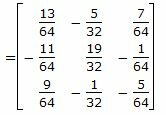Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда

Видео:Обратная матрицаСкачать

Обратная матрица

Содержание:

Видео:Обратная матрица (2 способа нахождения)Скачать

Обратная матрица

Миноры первого порядка можно определить для любой (не только квадратной) матрицы. Матрица может иметь много миноров, причём некоторые из них могут равняться нулю, а другие — нет.

Высший порядок минора матрицы, который не равен нулю, называют рангом матрицы.

Пример.

а) Рассмотрим матрицу:

Матрица не имеет миноров третьего порядка, но имеет три минора второго порядка, которые равны нулю

Следовательно, ранг матрицы

б) Рассмотрим матрицу:

Минор 3-го порядка этой матрицы, то есть её определитель, равный нулю:

Рассмотрим миноры 2-го порядка:

Видим, что существует минор 2-го порядка, отличный от нуля. Следовательно,

Очевидно, что ранг матрицы не может превышать её порядок.

Ранги транспонированных матриц совпадают.

Можно доказать, что ранг матрицы равный максимально возможному числу её линейно независимых строк (столбцов). Так, в приведённом нами примере строки 1 -1 3 и 4 -1 5 дают в сумме строку 3 0 2, то есть строки матрицы линейно зависимы.

Матрица, ранг которой меньше её порядка, называется вырожденной матрицей (это матрица, определитель которой равен нулю).

Для невырожденных матриц (а такими могут быть только квадратные) вводят понятие обратной матрицы.

По аналогии с умножением чисел, обратной для матрицы А называют матрицу , если

Для матрицы А обратной будет матрица:

где алгебраические дополнения элементов матрицы А.

Замечание.

1. Алгебраические дополнения элементов рядов матрицы стоят в соответственных столбцах, то есть проведена операция транспонирования.

2. Если в уравнении выполнять одинаковые элементарные преобразования строк матриц А и Е до тех пор, пока матрица А не преобразуется в единичную, то уравнение примет вид где преобразованная единичная матрица. Потому, что получим , то есть обратная матрица — это преобразованная единичная.

Свойства обратных матриц

Последнее свойство легко доказывается. Действительно, согласно свойствам определителей известно, что

Пример 1. Найти матрицу, обратную к матрице А:

Решение.

а) Установить, не будет ли вырожденной матрица А; для этого вычислим

Определитель отличный от нуля, поэтому для матрицы А существует

б) Вычислить алгебраические дополнения соответствующих элементов матрицы А:

в) Запишем матрицу М, составленную из алгебраических дополнений элементов матрицы А:

г) Запишем обратную матрицу транспонировав матрицу М:

д) Необходимо проверить правильность выполнения операции, то есть проверить, что

Следовательно, обратная матрица найдена правильно.

Пример 2. Найти обратную матрицу для матрицы А:

Решение. Запишем параллельно матрицы А и Е и выполним над ними одинаковые элементарные преобразования, направленные на преобразование матрицы А в единичную:

— умножим первый ряд матриц А и Е на три и отнимем от второго ряда соответствующей матрицы:

— сложим вторые ряды матриц А и Е с первыми:

— умножим вторые ряды на

В результате приведённых выше преобразований из единичной матрицы Е мы получили матрицу, обратную матрице А:

Проверим правильность нахождения обратной матрицы, вычислив её согласно схеме, приведённой в примере 1:

— вычислим определитель матрицы

— вычислим алгебраические дополнения элементов матрицы А:

— сложим матрицу М, составленную из алгебраических дополнений и транспонируем её:

— запишем обратную матрицу для матрицы А:

Как видим, матрицы совпадают.

Системы n линейных уравнений с n неизвестными

Определение. Линейным уравнением с n неизвестными называют уравнения вида:

где коэффициенты уравнения; неизвестные; свободный член.

В курсе средней школы рассматривали линейные уравнения с одним, двумя и тремя неизвестными. Это уравнения:

Геометрически эти уравнения изображают точку на числовой прямой, прямую на площади, площадь в пространстве.

Решением линейного уравнения считают совокупность значений неизвестных этого уравнения, которые преобразуют его в истинную тождественность.

Системой линейных уравнений называют два или более уравнений, которые решаются совместно. Это означает, что решением системы будут те решения её уравнений, которые удовлетворяют все уравнения системы. (сечение решений уравнений системы).

В общем виде система m линейных уравнений имеет вид:

где неизвестные; коэффициенты систем; свободные члены.

Систему можно представлять как произведение матриц:

Такую запись системы называют матричной формой записи.

Если ввести обозначения

то систему можно записать в виде матричного равенства:

Система называется однородной, если все свободные члены равны нулю (АХ=0).

Системы называется квадратной, если n=m (количество равенств и количество неизвестных равны).

Не каждая система имеет решения, например система состоящая из следующих уравнений:

решений не будет иметь.

Система называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет ни одного решения.

Если совместная система имеет только одно решение, то она называется определённой.

Однородная система всегда совместная, она имеет так называемое тривиальное решение

Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из её коэффициентов меньше чем число n её столбцов.

Квадратная однородная система имеет нетривиальное решение, только тогда когда определитель матрицы, составленной из её коэффициентов равен нулю.

Вопрос совместимости системы линейных уравнений полностью решается следующей теоремой.

Теорема Кронекера — Капелли

Для того, чтобы система была совместимой, необходимо и достаточно чтобы ранг основной матрицы А совпадал с рангом расширенной матрицы (матрица А, к которой присоединён столбец свободных чисел).

Доказательство. Рассмотрим матрицы А и :

Минор, который определяет ранг матрицы А входит в матрицу , следовательно ранг матрицы или равен матрице А, или на единицу больше него.

Необходимость. Если система А совместимая, то существуют значения неизвестных которые и являются решениями. Подставив эти значения в систему, получим m тождеств, из которых видно, что последний столбец матрицы является суммой всех последних столбцов, взятых вместе с коэффициентами (линейной комбинацией столбцов матрицы А). Определитель, у которого столбцы линейно зависимы равен нулю. Следовательно, ранг матриц совпадает.

Достаточность. Пусть ранги матриц А и совпадают. Это значит, что количество линейно независимых столбцов у этих матриц одинаковое. Потому, что матрицы отличаются только последним столбцом матрицы , существуют числа , такие, что сумма столбцов матрицы А взятых вместе с этими числами, равна столбцу свободных членов из системы . Следовательно, числа являются решениями системы.

Отметим, что совместная система имеет единое решение тогда и только тогда, когда ранг матрицы А равен числу неизвестных.

Пример 1. Установить совместимость системы:

Решение. Ранг матрицы, составленной из коэффициентов системы равен 2. Ранг расширенной матрицы равен 3, поскольку

Ответ: система несовместима.

Пример 2. Установить совместимость системы:

Решение. Ранг матрицы, составленной из коэффициентов системы равен 2, то есть равен числу коэффициентов. Ранг расширенной матрицы 2. Следовательно, система совместима и имеет единое решение.

Ответ: система совместима.

Пример 3. Установить совместимость системы:

Решение. Ранг матрицы, составленной из коэффициентов системы 2. Ранг расширенной матрицы 2.

Ответ: система совместима.

Решение систем n линейных уравнений с n неизвестными

1. Матричный метод. Одним из способов решения систем линейных уравнений является её умножение на обратную матрицу.

Пусть дана система6

Умножим правую и левую части на А -1 :

А -1 (АХ)=А -1 В или (А -1 А)Х=А -1 В.

Потому что, А -1 А=Е, получим

Нахождение обратной для матриц высоких порядков достаточно сложное, поэтому матричный метод используют довольно редко.

Пример 1. Решить систему:

Решение.

а) Запишем систему в матричной форме:

б) Вычислим определитель матрицы А:

в) Запишем обратную матрицу А -1 :

Обратная матрица найдена правильно, поскольку

г) Вычислим произведение матрицы А -1 В:

Ответ: х=2, у=1, z=3.

2. Метод Крамера. Пусть дана система (запишем в виде матричного уравнения) n линейных уравнений с n неизвестными

где определитель матрицы матрица, составленная из алгебраических дополнений элементов матрицы А:

Как видим, полученные выражения для элементов матрицы Х — это разложения элементов i-ой строки некоторого определителя, а именно:

где определитель матрицы А, а определитель матрицы, в которой столбец коэффициентов, которые стоят при заменён на столбец свободных членов (матрица В).

Если , то система будет иметь единое решение.

Если , то система или неопределённая, или несовместимая. Система будет несовместимой (не будет иметь ни одного решения), если хотя бы один из .

Если же, и , то система будет иметь множество решений (неопределённая)

Пример. Найти решения системы:

Решение.

а) Вычислим определитель матрицы А:

б) Вычислим определитель . Для этого первый столбец матрицы А заменим на столбец свободных членов (матрицей В) и для получения матрицы вычислим определитель:

в) Вычислим определители . Для этого заменим соответствующие столбцы матрицы А на столбец свободных членов и вычислим определители полученных матриц:

г) Найдём значения неизвестных

Ответ:

3. Метод Гаусса. Суть метода Гаусса заключается в последовательном изъятии неизвестных из уравнения системы. Поясним на примере системы трёх уравнений:

Разделим коэффициенты первого уравнения на . Получим систему:

Если теперь последовательно перемножить первое уравнение на коэффициенты и отнять соответственно от второго и третьего уравнения системы, то получим:

Неизвестное х мы изъяли из второго и третьего уравнения системы.

Изымем таким же способом у: разделим второе уравнение на , а потом, умножив на , отнимем от третьего. Получим:

Из третьего уравнения находим z, со второго — у, с третьего — х.

Алгоритм можно применять к системам более высоких порядков.

На практике, при непосредственном вычислении удобно использовать расширенную матрицу системы:

которую с помощью элементарных преобразований приводят к виду:

Пример 1. Решить систему уравнений:

Решение. Коэффициент системы равен 1, поэтому выпишем расширенную матрицу:

Умножим первую строку на 2 и отнимем от второй:

а потом умножим первую строку на 3 и отнимем от третьей:

Продолжим изымать переменные со второго и третьего уравнений системы (со второй и третьей строки расширенной матрицы). Коэффициент равен 1, поэтому просто умножим вторую строку на 5 и отнимем от третьей:

Система свелась к виду:

Из третьего уравнения системы находим z=1, подставив найденное значение во второе уравнение системы найдём у= -2, а из первого уравнения — х=3.

Ответ: х=3, у= -2, z=1.

Пример2. Решить систему уравнений:

Решение. Выпишем расширенную матрицу системы:

Разделим первую строку системы на коэффициент . Получим:

Умножим первую строку матрицы последовательно на 4 и 2 и отнимем соответственно от второй и третьей строк:

Разделим третью строку полученной матрицы на . Получим:

Умножим вторую строку матрицы на и отнимем её от третьей строки:

Начальная система свелась к виду:

Из третьего уравнения получим z=1, со второго — у=1, с первого х=1.

Ответ: х=1, у=1, z=1.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Обратная матница и её определение

Квадратная матрица называется обратной квадратной матрице если выполняется условие где единичная матрица. Квадратная матрица называется невырожденной или неособенной, если ее определитель отличен от нуля. Если определитель матрицы равен нулю, она называется вырожденной или особенной.

Всякая невырожденная квадратная матрица

имеет единственную обратную матрицу

где алгебраическое дополнение элемента матрицы . (Алгебраическое дополнение элементов каждой строки матрицы записаны в столбец с тем же номером).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Чтобы найти матрицу, обратную данной, необходимо:

1) вычислить определитель данной матрицы; 2) найти алгебраические дополнения ее элементов 3) составить матрицу из алгебраических дополнений взятых в том же порядке, что и элементы в матрице 4) в матрице поменять ролями строки и столбцы, записать матрицу каждый элемент матрицы разделить на определитель матрицы Рангом матрицы называется наивысший из порядков ее миноров, отличных от нуля. Ранг матрицы обозначается так: или .

Возможно вам будут полезны данные страницы:

🎥 Видео

8. Обратная матрицаСкачать

Матричный метод решения систем уравненийСкачать

Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать

Обратная матрица #1Скачать

Линейная алгебра, 9 урок, Метод ГауссаСкачать

Обратная матрица ➜ 2 способа и проверкаСкачать

Как находить обратную матрицу - bezbotvyСкачать

Обратная матрица 2x2Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение матричных уравненийСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Решение системы уравнений методом ГауссаСкачать

Урок 2. Обратная матрица: метод Гаусса, алгебраическое дополнение | Высшая математика | TutorOnlineСкачать

Нахождение обратной матрицы с помощью элементарных преобразованийСкачать