Тренажер по теме иррациональные уравнения 10 класс с ответами (2 видео)

Зачёт по теме «Решение иррациональных уравнений»

Зачётные задания по теме «Решение иррациональных уравнений» предназначены для проверки уровня знаний, умений и навыков учащихся 10 или 11 класса по данной теме и могут помочь выпускникам при подготовке к ЕГЭ. При решении заданий данного зачётного задания необходимо хорошо знать и уметь применять на практике основные алгоритмы решения иррациональных уравнений. В тесте представлены два варианта, в каждом из которых четырнадцать уравнений, и ответы к ним.

Устная (теоретическая) часть зачёта

1. Какое уравнение называют иррациональным?

2. Какое условие накладывается на подкоренное выражение корня чётной степени?

3. Какое условие накладывается на ту часть иррационального уравнения, которая не находится под корнем?

4. Как называется числовое значение неизвестного, удовлетворяющее уравнению с одним неизвестным?

5. Какие алгоритмы решения иррационального уравнения вы знаете?

Содержание

Минпросвещения планирует использовать технологию проведения ЕГЭ при организации олимпиад
Подготовка к приёмной кампании: что стоит знать абитуриенту?
Заметка 836
Тренажер по теме иррациональные уравнения 10 класс с ответами
Тест с ответами: “Иррациональные уравнения”
💡 Видео

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Минпросвещения планирует использовать технологию проведения ЕГЭ при организации олимпиад

Минпросвещения планирует использовать технологию проведения единого государственного экзамена при организации регионального и федерального этапов всероссийской олимпиады школьников. Об этом заявила замминистра просвещения Анастасия Зырянова на встрече в Общероссийском народном фронте.

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Подготовка к приёмной кампании: что стоит знать абитуриенту?

Что необходимо проверить в рейтинговых списках? Где искать самую оперативную информацию по поступлению? И как пройти приемную кампанию без стресса? На эти и другие вопросы ответил начальник управления организации приема абитуриентов Московского городского педагогического университета Евгений Татаринцев.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Заметка 836

В день проведения экзамена (в период с момента входа в ППЭ и до окончания экзамена) в ППЭ участникам экзамена запрещается иметь при себе уведомление о регистрации на экзамены (необходимо оставить в месте для хранения личных вещей, которое организовано до входа в ППЭ, или отдать сопровождающему), средства связи, электронно-вычислительную технику, фото-, аудио- и видеоаппаратуру, справочные материалы, письменные заметки и иные средства хранения и передачи информации, выносить из аудиторий письменные заметки и иные средства хранения и передачи информации, из ППЭ и аудиторий ППЭ запрещается выносить экзаменационные материалы, в том числе КИМ и черновики на бумажном или электронном носителях, фотографировать экзаменационные материалы.

Рекомендуется взять с собой на экзамен только необходимые вещи. Иные личные вещи участники экзамена обязаны оставить в специально выделенном месте (помещении) для хранения личных вещей участников экзамена в здании (комплексе зданий), где расположен ППЭ.

Участники экзамена занимают рабочие места в аудитории в соответствии со списками распределения. Изменение рабочего места запрещено.

Во время экзамена участникам экзамена запрещается общаться друг с другом, свободно перемещаться по аудитории и ППЭ, выходить из аудитории без разрешения организатора.

При выходе из аудитории во время экзамена участник экзамена должен оставить экзаменационные материалы, черновики и письменные принадлежности на рабочем столе.

Участники экзамена, допустившие нарушение указанных требований или иные нарушения Порядка, удаляются с экзамена.

Видео:Иррациональные уравнения. Видеоурок 8. Алгебра 10 классСкачать

Тренажер по теме иррациональные уравнения 10 класс с ответами

Дидактические материалы

11 класс

Алгебра и начала анализа ( авторы учебника А.Н.Колмогоров, А.М.Абрамов и др.)

Геометрия (авторы учебника Л.С.Атанасян, В.Ф.Бутузов и др..)

Алгебра (авторы учебника Ю.Н.Макарычев, Н.Г.Миндюк и др.)

Контрольная работа по теме: «Квадратный трёхчлен и его корни» (в форме ЕГЭ)

Контрольная работа по теме: «Квадратные уравнения» (в форме ЕГЭ)

Контрольная работа по теме: «Квадратные неравенства» (в форме ЕГЭ)

Алгебра (авторы учебника Ш.А.Алимов и др.)

Алгебра (авторы учебника Ш.А.Алимов)

Геометрия (авторы учебника Л.С.Атанасян, В.Ф.Бутузов и др..)

Алгебра (авторы учебника Ш.А.Алимов)

Алгебра (авторы учебника Ю.Н.Макарычев, Н.Г.Миндюк и др.)

Геометрия (авторы учебника Л.С.Атанасян, В.Ф.Бутузов и др..)

Тренажер по теме иррациональные уравнения 10 класс с ответами

Мониторинг качества знаний по математике

11 класс

«Бог создал единицу,

а остальные числа

Цели урока:

— обеспечить повторение, обобщение и систематизацию материала темы; создать условия контроля (самоконтроля) усвоения знаний и умений;

— способствовать формированию умений применять знания в новой ситуации, развитию математического кругозора, мышления и речи, внимания и памяти;

— содействовать воспитанию интереса к математике, активности творчества.

Оборудование:

— записи на доске,

— учебник «Математика-5» (Г.В.Дорофеев, Л.Г.Петерсон),

— дидактические материалы по математике 5 класс (в тексте ДМ),

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Тест с ответами: “Иррациональные уравнения”

1. Найдите корень уравнения:

а) 38 +
б) 16
в) 22

2. Найдите корень уравнения:

3. Найдите корень уравнения: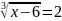

а) 12
б) 18
в) 14 +

4. Найдите корень уравнения: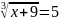

а) 116 +
б) 88
в) 94

5. Решите уравнение: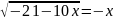

Если уравнение имеет больше одного корня, в ответе запишите больший из корней:
а) 3
б) 5
в) -3 +

6. Решите уравнение: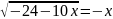

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) 6
б) -6 +
в) -12

7. Решите уравнение:

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) -15
б) 5
в) -5 +

8. Решите уравнение: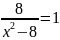

Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
а) 4 +
б) -4
в) 8

9. Решите уравнение: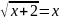

Если уравнение имеет больше одного корня, в ответе запишите меньший из корней:
а) 4
б) -2
в) 2 +

10. Иррациональными называются уравнения, в которых переменная содержится под знаком корня, так ли это:
а) да +
б) нет
в) отчасти

11. Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства, так ли это:
а) да +
б) нет
в) зависит от условия задачи

12. Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень, так ли это:
а) да +
б) нет
в) зависит от условия задачи

13. При возведении уравнения в степень могут появиться посторонние корни. Поэтому необходимой частью решения иррационального уравнения является проверка, так ли это:
а) да +
б) нет
в) зависит от условия задачи

14. Один из методов решения иррациональных уравнений:
а) метод введения старых переменных
б) метод введения новых переменных
в) метод введения новых переменных +

15. Один из методов решения иррациональных уравнений:
а) переход к равносильной системе (в этом случае проверка не нужна) +
б) метод введения старых переменных
в) метод возведения обеих частей уравнения в разные степени

16. Один из методов решения иррациональных уравнений:
а) метод возведения обеих частей уравнения в разные степени
б) метод возведения обеих частей уравнения в одну и ту же степень +
в) метод введения новых переменных

17. Правильно решите: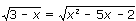

а) 1
б) 4
в) -1 +

18. Правильно решите: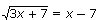

а) -14
б) 14 +
в) 28

19. Правильно решите: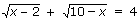

а) 12
б) -6
в) 6 +

20. Правильно решите: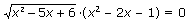

а) 4
б) +
в) 5

21. Правильно решите: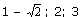

а) 7 +
б) -7
в) 14

22. Алгебраическое уравнение называется иррациональным, если оно содержит переменные под знаком корня или в основе степени с дробным показателем, так ли это:
а) нет
б) да +
в) отчасти

23. Какое из перечисленных чисел является иррациональным:
а) 1/2
б) 0
в) √5 +

24. Как называется уравнение, содержащее неизвестное в определенной дробной степени:
а) рациональное
б) иррациональное +
в) дробное

25. Уравнение называется алгебраическим, если обе его части – … выражения:
а) математические
б) равнозначные
в) алгебраические +

26. Область допустимых значений (сокращённо ОДЗ) уравнения есть множество значений переменной, при которых обе части данного уравнения имеют смысл, так ли это:
а) нет
б) да +
в) отчасти

27. В большинстве ситуаций специально искать ОДЗ:
а) не нужно искать +
б) нужно искать
в) по желанию

28. Основной метод решения иррациональных уравнений:
а) метод утроения радикала
б) метод удвоения радикала
в) метод уединение радикала +

29. При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может, так ли это:
а) да +
б) нет
в) отчасти

30. Иррациональные числа невозможно представить в виде дроби, так ли это:
а) нет
б) да
в) отчасти