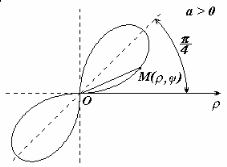
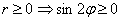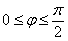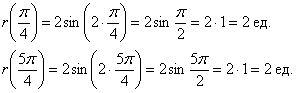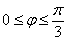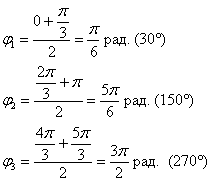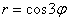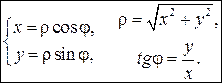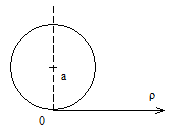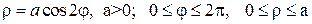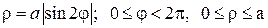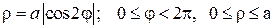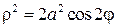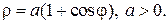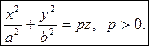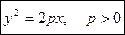Совершенно верно, речь пойдёт о цветке с лепестками:
Построить линии, заданные уравнениями в полярных координатах
а) 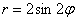
б)
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Решение:
а) Найдём область определения функции:
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции 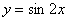
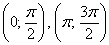
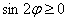
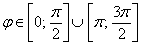
Вообще говоря, решение рассматриваемых неравенств представляет собой бесконечное множество отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до 
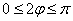
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– найденный отрезок 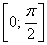
– следующий интервал 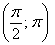
– следующий отрезок 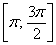
– и, наконец, интервал 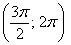
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
Итак, 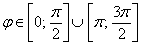
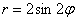
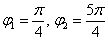
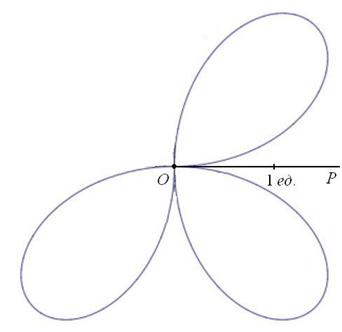
Вот закономерный результат заботливого садовника:
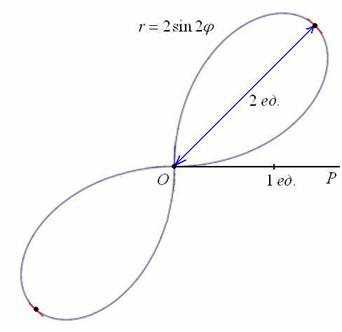
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения 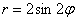
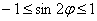
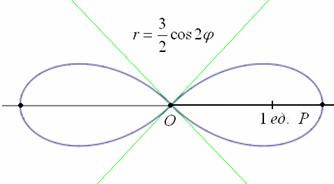
б) Построим линию, заданную уравнением 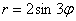
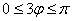
Далее начинаем «нарезку пирога кускам» по 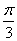
– отрезок 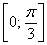
– интервал 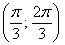
– отрезок 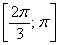
– интервал 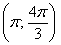
– отрезок 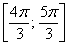
– интервал 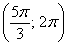
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: 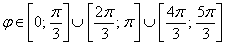
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина 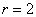
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов:
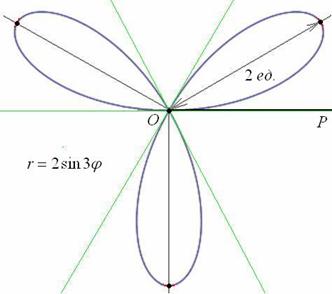
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида 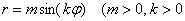


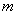
Например, уравнение 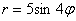
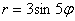
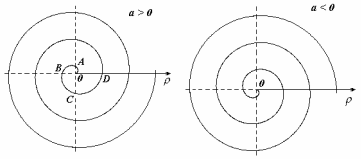
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если 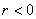
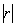
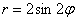
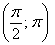
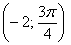
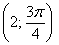
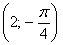
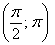
И, соответственно, когда угол проходит значения 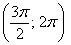
Интересно отметить, что при таком подходе вторая полярная роза 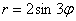
Сформулируем правило розы для обобщенной системы координат: уравнение вида 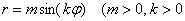

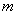
1) если 
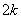
2) если 

Например, роза 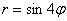
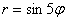
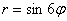
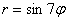
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Построить линии, заданные уравнением в полярных координатах
а) 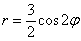
б)
Сформулировать общее правило о количестве и длине лепестков полярной розы вида 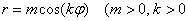

В моём образце решение проведено 1-ым способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций 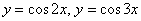
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найдённые секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-ой части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3: Решение: найдём область определения:
Вычислим полярные координаты точек, принадлежащих данной линии:
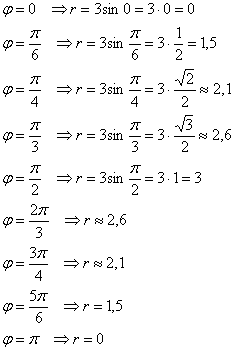
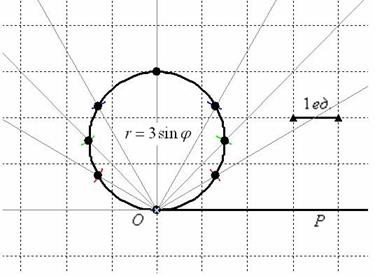
Выполним чертёж:
Найдём уравнение линии в декартовой системе координат:
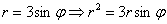
Проведём замены 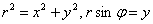
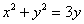
Выделим полный квадрат:
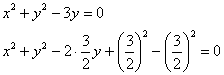
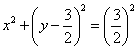
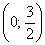
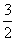
Дополнительная информация: уравнение вида 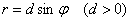
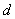
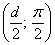
Пример 5: Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргументнаходится в пределах от 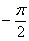
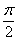
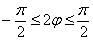
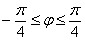
Таким образом:
– отрезок 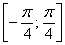
– интервал 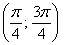
– отрезок 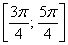
– интервал 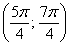
Область определения: 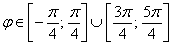
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна 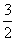
б) область определения: 
Выполним чертёж:
Уравнение вида 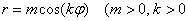


Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
- Линии в полярной системе координат
- Исследовательская работа «Розы Гвидо Гранди»
- Рассмотрим уравнение кривой
- Рассмотрим уравнение кривой
- Замечательные кривые
- Применение полярных координат
- В фотографии
- В экономике
- В военном деле
- В медицине
- В системах идентификации человека
- В различных областях науки и техники
- В математическом дизайне и архитектуре малых форм
- В ландшафтном дизайне
- 🌟 Видео
Видео:Полярная система координатСкачать

Линии в полярной системе координат


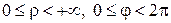
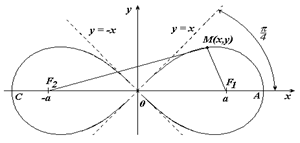
Связь полярных координат с декартовыми
M(x,y) и M( 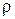
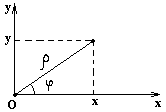 |
 |
Окружности


Спирали
 |
Архимедова спираль: 
Гиперболическая спираль: 
Логарифмическая спираль: 
Розы
Двухлепестковые розы: 
Четырехлепестковые розы a > 0
 |  |
 |
 |
Лемниската Бернулли
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
Кардиоида
В полярных координатах
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 
Параметрическое задание линий
Окружность
 |

Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
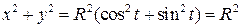
Циклоида


При 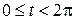

Астроида
 |
где
В декартовых координатах уравнение астроиды
Длина астроиды L=6R, а площадь, ограниченная астроидой S=3pR 2 /8.
IV. Поверхности второго порядка
Эллипсоид
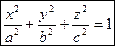
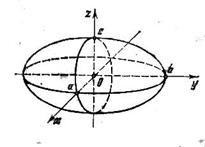 |
Гиперболоиды
Однополостный гиперболоид

 |
Двуполостный гиперболоид

|
Параболоиды
Эллиптический параболоид
 |
Гиперболический параболоид
Конус
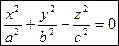
 |
Цилиндры
Эллиптический цилиндр
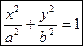
 |
Гиперболический цилиндр

 |
Параболический цилиндр
 |
1. Ильин В.А. Аналитическая геометрия / В.А.Ильин, Э.Г.Позняк.
М.: Наука, ГФМЛ, 1988.
2. Бугров Е.С. Элементы линейной алгебры и аналитической геометрии /
Е.С. Бугров, С.М. Никольский. М.: Наука, 1984.
3. Бугров Е.С. Высшая математика: Задачник / Е.С. Бугров, С.М. Никольский. М.: Наука, 1982.
4. Сборник задач по математике для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. — 4-е изд., перераб. и доп. — М.: Физматлит, 2003. — 288 с.: ил.; 21 см. — ISBN 5-940520-34-0.
5. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры /
Д.В.Беклемишев. М.: Наука, 1984.
6. Наумов В.А. Руководство к решению задач по линейной алгебре и аналитической геометрии / В.А.Наумов. М.: Наука, 1993.
7. Фадеев Д.К. Сборник задач по высшей алгебре / Д.К. Фадеев, Н.С. Соминский. М.: Наука, 1997.
8. Беклемишева Л.А. Сборник задач по аналитической геометрии и линейной алгебре / Л.А. Беклемишева, А.Ю. Петрович, И.А. Чубаров. М.: Наука, 1987.
9. Кузнецов Л.А. Сборник заданий по высшей математике / Л.А. Кузнецов М.: Высшая школа, 1994.
10. Минорский В.П. Сборник задач по высшей математике / В.П. Минорский. М.: Физматгиз, 1961.
11. Клетенник Д.В. Сборник задач по аналитической геометрии /
Д.В. Клетенник. М.: Наука, 1986.
12. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии /
О.Н. Цубербиллер. М.: Наука, 1970.
13. Косторкин А.И. Линейная алгебраическая геометрия / А.И. Косторкин,
Ю.И. Манин. М.: Наука, 1986.
14. Бахвалов С.Б. Сборник задач по аналитической геометрии /
С.Б. Бахвалов, П.С. Моденов, А.С. Пархоменко. М.: Наука, 1964.
Соболев Александр Борисович
Вигура Марина Александровна
Рыбалко Александр Федорович
Рыбалко Наталья Михайловна
Трояновская Людмила Юрьевна
Кассандров Игорь Николаевич
Дисциплина: ЕН.Ф.01 Математика. алгебра и геометрия
Модуль 2: Векторная алгебра. Геометрия: аналитическая геометрия в пространстве, на плоскости, кривые второго порядка, поверхности.
Подписано в печать Формат 60×84 1/16
Бумага писчая Плоская печать Усл.печ.л. 3,13
Уч.-изд.л. 2,6 Тираж Заказ Цена “C”
Редакционно-издательский отдел ГОУ ВПО УГТУ–УПИ
620002, Екатеринбург, ул. Мира, 19
ООО «Издательство УМЦ УПИ»620002, Екатеринбург, ул. Мира, 17
Видео:Построение кривой в полярной системе координатСкачать

Исследовательская работа «Розы Гвидо Гранди»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
САМАРСКИЙ КОЛЛЕДЖ СТРОИТЕЛЬСТВА И ПРЕДПРИНИМАТЕЛЬСТВА (ФИЛИАЛ) ФГБОУ ВО «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
РОЗЫ ГВИДО ГРАНДИ
Окунев Игорь, студент Самарского колледжа строительства и предпринимательства ФГБОУ ВО «Национальный исследовательский Московский государственный строительный университет». Научный руководитель – Егорова Н. С., преподаватель естественно-научных дисциплин.
1. Введение. Цель и задачи работы
2. Основная часть
2.1 Историческая справка
2.2 Разнообразие роз Гвидо Гранди
2.3 Полярная система координат
2.4 Общие свойства роз Гвидо Гранди
2.5 Связь с другими замечательными кривыми
«Узоры математики, как и узоры художника или узоры поэта, должны быть красивы, идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики» (Дж.Х. Харди).
Математика-это наука, которая изучает величины, количественные отношения и пространственные формы, описывает процессы, происходящие в окружающем нас мире. Законы математики и решения математических задач приложены ко всем областям человеческой деятельности. Линии занимают особое положение в математике. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удается решать многие научные, инженерные задачи в различных отраслях жизни. Меня заинтересовали кривые, заданные в полярных координатах. Среди них можно назвать спираль Архимеда, логарифмическую спираль, кардиоиду, лемнискату, астроиду, розы Гвидо Гранди. Больше других мое внимание привлекла математическая кривая, похожая на цветок — полярная роза или роза Гвидо Гранди, и я в своей работе хочу исследовать многообразие форм «роз» Гвидо Гранди.
Исследовать, как изменяются кривые Гвидо Гранди, заданные в полярной системе координат в зависимости от различных значений параметров
1. Установить связь между количеством лепестков, их формул и симметричности получившегося рисунка.
2. Получить большое разнообразие форм «роз» Гвидо Гранди.
3. Изучить использование полярных координат в жизни, искусстве, науке, технике и применить на практике.
2.1 Историческая справка
В 18 веке итальянский геометр Гвидо Гранди (1671-1742) создал кривые линии с точными плавными очертаниями. Они были похожи на цветок. Семейство этих кривых было названо семейством роз Гвидо Гранди. Их точные черты не причуды природы, они предопределены особо подобранными математическими зависимостями. Эти зависимости были подсказаны самой природой, ведь в большинстве случаев абрис листа или цветка представляет собой кривую, симметричную относительно оси. Свои очаровательные цветы Гвидо Гранди собрал в одну книгу и назвал ее «Цветник роз» . Гранди извест ен своей работ ой «Flores geometrici» (1728). Данная работа позволяет изучать крив ые , котор ые име ю т форму лепестков цветка. Он назвал розы кривой rhodonea и назвал крив ую Clelia в честь графин и Клели и Борромео .
Уравнение розы Гвидо Гранди в полярных координатах имеет вид
Задавая параметр 
2.2. Разнообразие роз Гвидо Гранди
Рассмотрим уравнение кривой
Возьмём для начала любое a и k -чётное число, тогда получим «розу» с количеством лепестков 2 k , и длина от начала координат до вершины лепестков будет равна радиусу описанной окружности a . Кривые симметричны относительно оси ординат, оси абсцисс и начала координат.
Если мы возьмём любое a и k -нечётное число, то получим цветок из k лепестков. Мы замечаем, что в одном случаи есть лепесток, направленный по оси ординат вверх, а в другом вниз. Это зависит от значения k . Вниз лепесток будет направлен при k =3 и при всех последующих нечётных через одно число, вверх – при k =5 и при всех следующих нечетных числах через одно. Кривые симметричны относительно оси ординат.
Рассмотрим уравнение кривой 
Мы замечаем, что количество лепестков стало зависеть от c и b .Если c=1, а b =2 получаем кривую, напоминающую 2 кардиоиды, «наползшие» друг на друга. Если b=3, то мы получим кардиоиду с петлей «внутри себя». Если b>3 мы получим закольцованную спираль, в центре которой будет кардиоида (1 или 2). Если c > b , c -любое нечётное число, b -любое нечётное число и получившаяся дробь не сокращается до целого числа, тогда мы получаем «розу» из c -лепестков, у которого они находят друг на друга. При c =5 и всех последующих нечётных чисел через одни, один лепесток «розы» будет направлении вниз по оси ординат. По аналогии при c =7 и при всех последующих нечётных числах один лепесток направлен вверх по оси ординат. Кривая симметрична относительно оси ординат.
Если c > b , c -любое чётное число, b -любое нёчетное и получившаяся дробь не сокращается до целого числа, то мы имеем «розу» из лепестков количеством 2 c . Они ложатся друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
Если мы зададим значения c > b , c -любое нечётное число, b -любое чётное и получившаяся дробь не сокращается до целого числа, тогда увидим цветы с количеством лепестков 2 c . Они будут накладываться друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
Рассмотрим уравнение кривой 
Если k -чётное число, и мы будем прибавлять | m |>5 , то наша «роза» из 2k лепестков будет переходить в кривую, стремящуюся к форме окружности. Чем больше m и чем меньше a , тем более округленный цветок мы получим
Если k -нечётное число, и если будем прибавлять числа | m |>5 , то наша кривая в форме цветка будет переходить в окружность. Чем больше m и чем меньше a , тем более округленный цветок мы получим.
2.3. Полярная система координат.
Положение любой точки P в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа (или другие символы), определяющие положение точки, называются координатами этой точки. В зависимости от целей и характера исследований выбирают различные системы координат. Рассмотрим полярную систему координат.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Итак: положительным направлением отсчета углов считается направление «против часовой стрелки»
Основными понятиями этой системы являются точка отсчёта – полюс, и луч, начинающийся в этой точке – полярная ось.
Полярный радиус ρ – длина отрезка О P
Полярный угол φ – величина угла между полярной осью и отрезком О P .
Переход от полярной системы координат к декартовой
Если полюс полярной системы координат совместить с началом прямоугольной системы координат, а полярную ось с положительной полуосью Ox, то по известным полярным координатам точки А (ρ;φ) её прямоугольные координаты вычисляются по формулам:
2.5 Общие свойства роз Гвидо Гранди
Семейство роз Гранди имеет свойство, которое в природе не сразу и заметишь: так как

то вся кривая расположена внутри круга единичного радиуса. В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 1.
Наиболее красивые «цветы» получаются при k = 2 (четырехлепестковая роза) и при k = 3 (трехлепестковая роза).
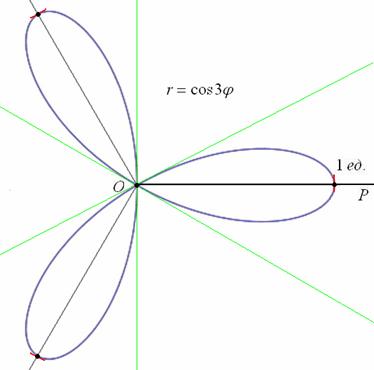
Покажем, как построить трёхлепестковую розу. Для построения этой кривой сначала заметим, что поскольку полярный радиус неотрицателен, то должно выполняться неравенство 

В силу периодичности функции 














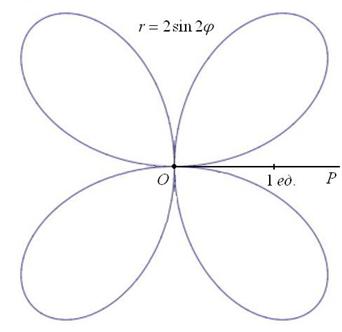
Рассмотрим теперь, как построить кривую, заданную в полярной системе координат уравнением ρ= sin(2 ∗ 𝜑) .
Функция 

поэтому достаточно построить кривую в первой четверти, потом зеркально отразить ее относительно оси Оу и использовать периодичность для построения кривой в третьей и четвертой четвертях.
Функция 


Отметим следующие интересные свойства четырехлепестковой розы:
• четырехлепестковая роза есть геометрическое место оснований перпендикуляров, опущенных из начала координат на отрезок длиной 1, концы которого скользят по координатным осям;
• площадь, ограничиваемая четырехлепестковой розой, равна 
Вообще, если k — натуральное число, то роза состоит из 2k лепестков при четном k и из k лепестков при k нечетном.
2.6.Связь с другими кривыми
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Замечательные кривые
Кардиоида (от греческих слов сердце и вид) – получила свое название из-за схожести своих очертаний со стилизованным изображением сердца.
Определяется уравнением в полярных координатах

(a — радиус окружности)
В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя в спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало ее изучению.
Определяется уравнением в полярных координатах:
(с – половина расстояния между фокусами лемнискаты)
Полярная роза – известная математическая кривая, похожая на цветок. Определяется уравнением в полярных координатах
Спираль Архимеда – названа в честь ее изобретателя, древнегреческого математика Архимеда. Определяется уравнением в полярных координатах
Видео:Видеоурок "Полярная система координат"Скачать

Применение полярных координат
В фотографии
Вертикальные линии после того, как к ним применен фильтр (переводящий координаты точек из прямоугольной системы в полярную), стали расходиться из центральной точки.
В экономике
Необычный формат биржевых графиков предложил в 1990-е годы российский математик Владимир Иванович Елисеев
Ф – время её совершения
Используя такую систему координат, относительно просто связать градусы и время (в году 365 дней, в окружности – 360 градусов)
В военном деле
Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y), геодезической (широта, долгота).
В медицине
Компьютерная томография сердца в системе полярных координат .
В системах идентификации человека
Результат преобразования кольца радужной оболочки из декартовой системы координат в полярную.
В различных областях науки и техники
Измерительный проектор предназначен для измерения различных параметров в прямоугольной и полярной системах координат
Применяется в измерительных лабораториях и цехах предприятий точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, а также в лабораториях НИИ.
В математическом дизайне и архитектуре малых форм
С помощью выращенных цветов, различных кривых в полярных координатах и графических редакторов можно сделать, например различные рисунки, рамки-орнаменты, или украсить ими различные предметы. Орнамент — украшение, узор, состоящий из ритмически организованных повторяющихся элементов, которые композиционно могут образовывать орнаментальный ряд.
В ландшафтном дизайне

2.7 Практическая часть
Так как я обучаюсь в Самарском колледже строительства и предпринимательства, то данная тема мне близка и актуальна. На отделении садово-парковое и ландшафтное строительство студенты создают эскизы и макеты цветников, клумб и альпийских горок. 
На отделении строительство зданий и сооружений, на уроках архитектуры изучают и создают современные орнаменты.
Мной созданы несколько эскизов орнамента. Изучение линий Гвидо Гранди натолкнуло меня выполнить эскизы орнамента в виде кардиоид и роз. Несколько моих разработок я здесь представлю.
🌟 Видео
Площадь фигуры, заданной в полярной системе координатСкачать

Площади 12Скачать

Глаза гипножабы и площадь фигур в полярной системе координатСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

§7 Розы ГрандиСкачать

§12 Полярное уравнение прямойСкачать

Полярная система координатСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Полярная система координат.Скачать

Полярные координаты. Полярное уравнение эллипса.Скачать

Скорость и ускорение точки в полярных координатахСкачать

§30 Уравнения кривых второго порядка в полярных координатахСкачать

Площадь пересечения эллипсов и двойной интеграл в полярной системе координатСкачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

§52 Полярная система координатСкачать

Полярная система координатСкачать